波浪特性及其能量计算方法

Van Dorn在参考文献[3]中给出了波浪及波浪谱物理学解释。在图4.5中，给出了两种周期不同的波浪特性。这两种波浪代表了波浪的主要类型。

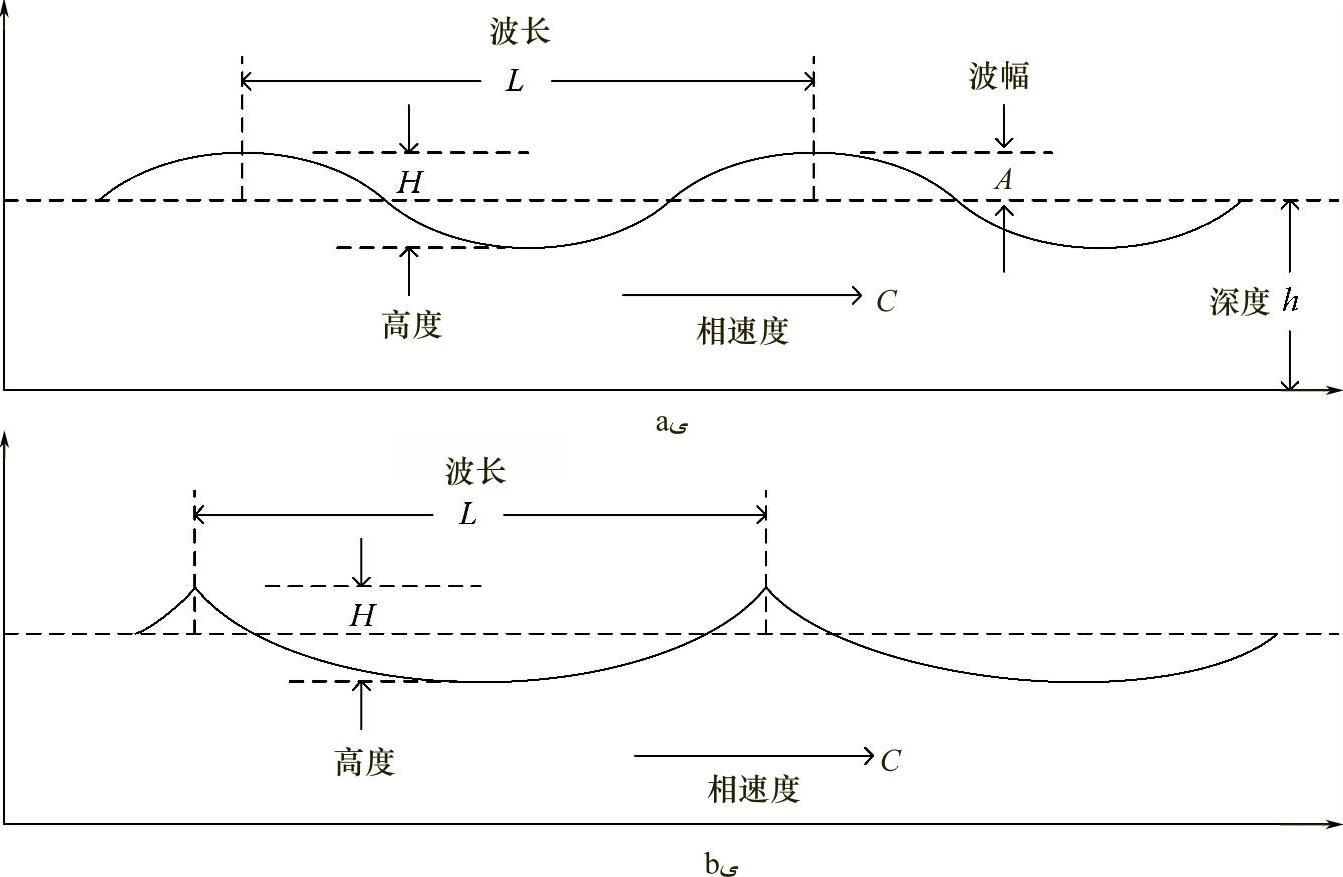
图4.5 波浪特性 （改编自W.J.Jones and M.Ruane，“Alternative electrical energy sources for Maine，Appendix I，Wave Energy Conversion by J.Mays，”Report No.MIT-E177-010，MIT Energy Laboratory，1977年7月）

图4.5a所示为类似于正弦曲线的周期性前进波，它对称于平衡水位。在图4.5b中，波浪周期较长，不再是正弦波或对称形式。它们的波峰顶部是尖的，在平衡水位之上的波幅要比又长又平滑的波谷更高，波峰下降之后就是波谷。

将单位波面宽度的势能和动能（J，标幺值）加在一起，就可以计算出海洋波浪的总能量。波长为L的波浪势能由其从平均海平面处产生的位移而得。波浪动能是水粒子横向运动和纵向运动叠加的结果^[4]。

海洋波浪的势能和动能总和可以表示为

式中 g——重力加速度（9.8m/s²）；

ρ——水的密度（1000kg/m³）；

A——波幅（m）。

将能量E乘以波浪的传播速度v_g，可以得到平均能通量或波浪周期能量：

(www.xing528.com)

式中 T——波浪周期（s）；

L——波长（m）^[4]。

下列离散关系描述了波浪周期T和波长L之间的联系：

如果将式（4.4）代入式（4.3），可以求得波浪能或者能通量：

除了使用波幅，波浪能量也可以表示为浪高的函数H。考虑到波幅是浪高的一半，因此波浪能量可以改写为

其他计算请参见参考文献[3]和[5]。