基于P&O的MPPT方法优化

在这种MPPT方法中，水流速度既不是通过传感器测得的，也不是通过处理器求得。在这种方法中，MPPT是通过控制降压变换器的占空比而得到的，如图3.65所示^[35，38]。

与潮汐流速值对应的潮汐水轮机特性为如图3.66所示的二阶方程曲线。潮汐发电机的输出功率在不同的潮汐流速下的潮汐发电机的特定转速处达到最大值。

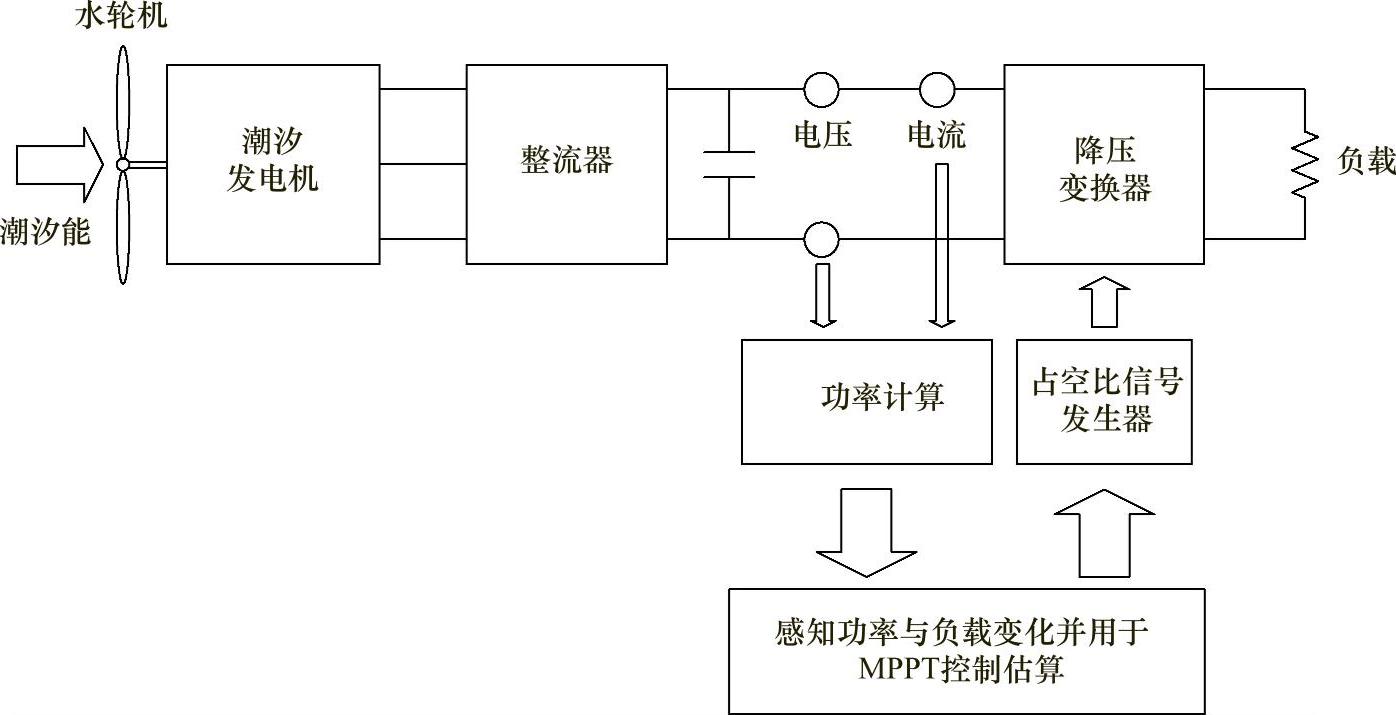
图3.65　MPPT控制系统框图

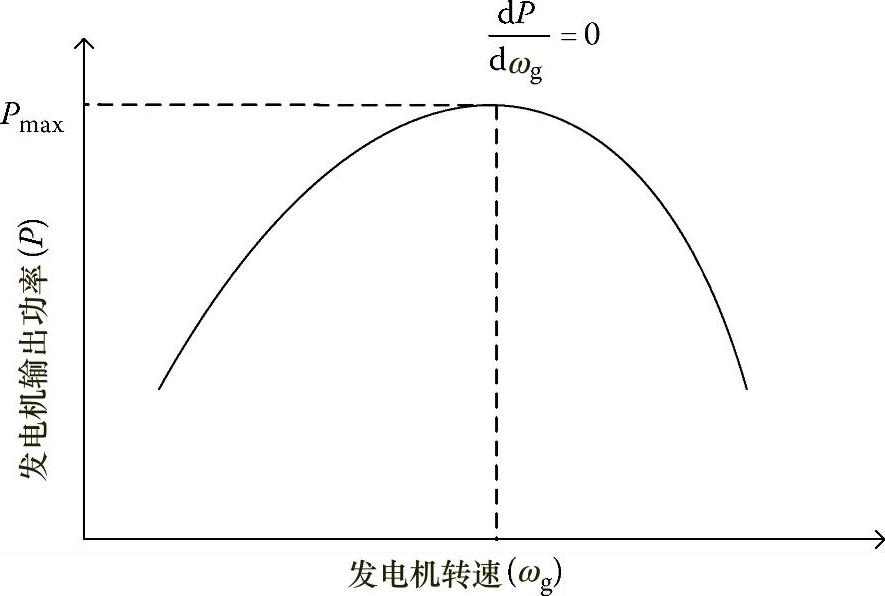
图3.66 潮汐水轮机转速—功率特性

当潮汐发电机输出功率的变化对发电机的转速变化等于零时，潮汐发电机可以产生最大功率：

应用链式法则^[39]，式（3.53）可表示为

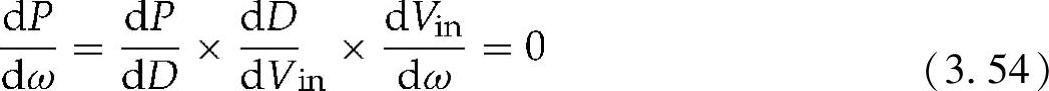
在这种方法中，不需要使用潮汐水轮机特性、潮汐速度测量、潮汐水轮机转速等信息。因此，这种方法可以克服基于查表或者流速计算的MPPT方法的缺点。

一个稳态运行的降压变换器占空比（D）可以表示为

式中 V_out——变换器的输出电压；

V_in——变换器的输入电压。

这个变换器的占空比在其输入电压方面的变化为(www.xing528.com)

三相整流输出电压与变换器输入电压相等。电压变化对转速变化是正向的。换句话说，它们是向同一方向变化的（增加或减少）：

使用式（3.75）、式（3.76）和式（3.73）可以得出

因此，潮汐能发电系统的MPPT控制可以通过占空比调节来实现。因此，过占空比的输出功率变化零点等于过发电机转速的输出功率变化的零点。

从图3.72可以看出，如果当前的发电机转速处于最佳转速的左侧，则应提高该发电机转速以使得发电机的输出功率达到最大功率点^[40]。这就意味着dP/dω应该大于零：

通过式（3.58）和式（3.59）可得，发电机转速变化及变换器的占空比与发电机输出功率的关系为

从图3.72可以看出，如果当前的工作点处于最佳转速的右侧，则应该降低变换器的占空比以达到最大功率点。在此例中，dP/dω必须小于零。在这种情况下，式（3.60）变为

根据式（3.60）和式（3.61），可以估计图3.72中发电机的转速位置（在左侧或者右侧）。然后，占空比将被调整，而且水轮机转速将达到最佳点。输出功率测量和占空比调整的过程不断重复。因此，通过控制接口DC-DC变换器的占空比就可以实现MPPT，如图3.66所示。

因此，这种方法并不直接依赖于水轮机特性与转速—功率曲线，因为它仅仅需要输出功率变化，而不是潮汐流和水轮机转速的测量值。