水轮机管道动力学模型优化

图3.24给出了水轮机动力学特性。水轮机有一个压力管道、无阻水头和尾水渠。根据结构设计的不同，水轮机可能会配有一个调压塔，也可能不配^[15，16]。

假设：流体（例如，水）是不可压缩的；非弹性水体（管道）的长度为L，截面积为A；压力管道中的损失记为h₁，它与流量的平方（q²）成正比；水头损失系数记为f_p，通常可以忽略不计。

根据动量定理，管道的流量变化可以表示为

式中 q——水轮机流量（m³/s）；

A——压力管道截面积（m²）；

L——压力管道长度（m）；

g——重力加速度（m/s²）；

h₀——水体的静水头（m）；

h——水轮机进口水头（m）；

h₁——管道摩擦的水头损失（m）。

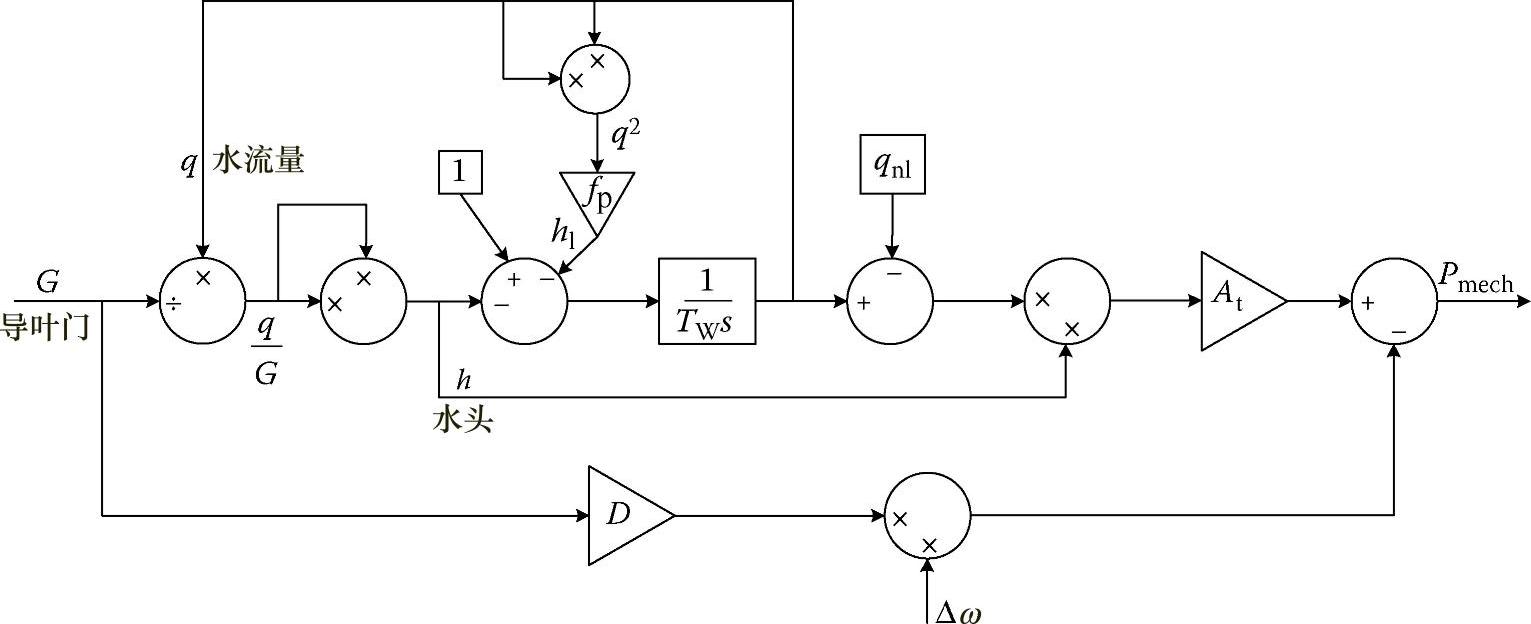
图3.24 非线性水轮机模型

水的时间常数定义为

式中 q_base——选择最大流量时水轮机上方的水体水头，最大流量出现在导叶门完全打开时（G=1）；

h_base——水轮机处的水头。

换句话说，基准水头是可用的总静水头，基准开度是导叶门的最大开度。基准数还可以采用其他任何参数。

式（3.3）中的每台机组表示变为

式中 h——水轮机水头；

h_l——每台机组的水头损失。

水轮机的水流量是开度和水头的函数：

每台机组系统中，流经水轮机的水流量为

(www.xing528.com)

在一个理想的水轮机中，机械功率等于流量乘以水头，还要考虑必要的转换因子。水轮机的效率自然是小于100%，因而有效流量就是无负载流量与实际流量之差。有效流量应乘以水头。导叶门开度对速度偏差阻尼也有影响，并会导致机械功率下降。机械功率可以表示为

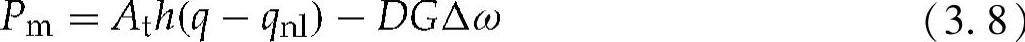
式中 q_nl——每台机组的无负载流量，代表固定功率损失；

A_t——式（3.9）给出的比例常数，可以根据水轮机额定功率（MW）和发电机基准功率（MVA）计算而得：

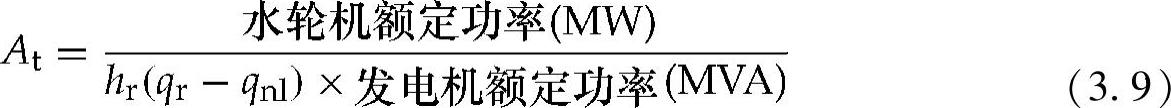
式中 h_r——水轮机在额定流量时的单台机组水头；

q_r——在额定负载时的单台机组流量，在额定负载时，单台机组的开度通常要小于所有机组的开度总和（1）。

式（3.9）定义了参数A_t，它代表了导叶门开度与单台机组水轮机功率之间在发电机MVA基准处的转换关系。

如果摩擦损失忽略不计，该非线性水轮机模型（见图3.24）可以简化为图3.25所示的线性化模型。

根据这个线性化简化模型，时间常数可以被定义为

而且

式中 G_o——工作点处的单台机组导叶门开度；

q_o——工作点处的单台机组稳态流量。

根据图3.25，基于这些时间常数，机械功率输出变为

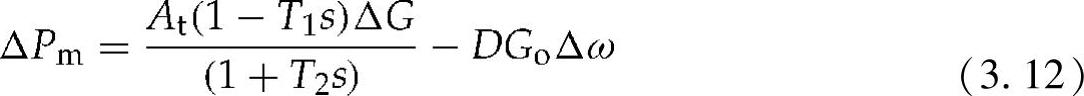
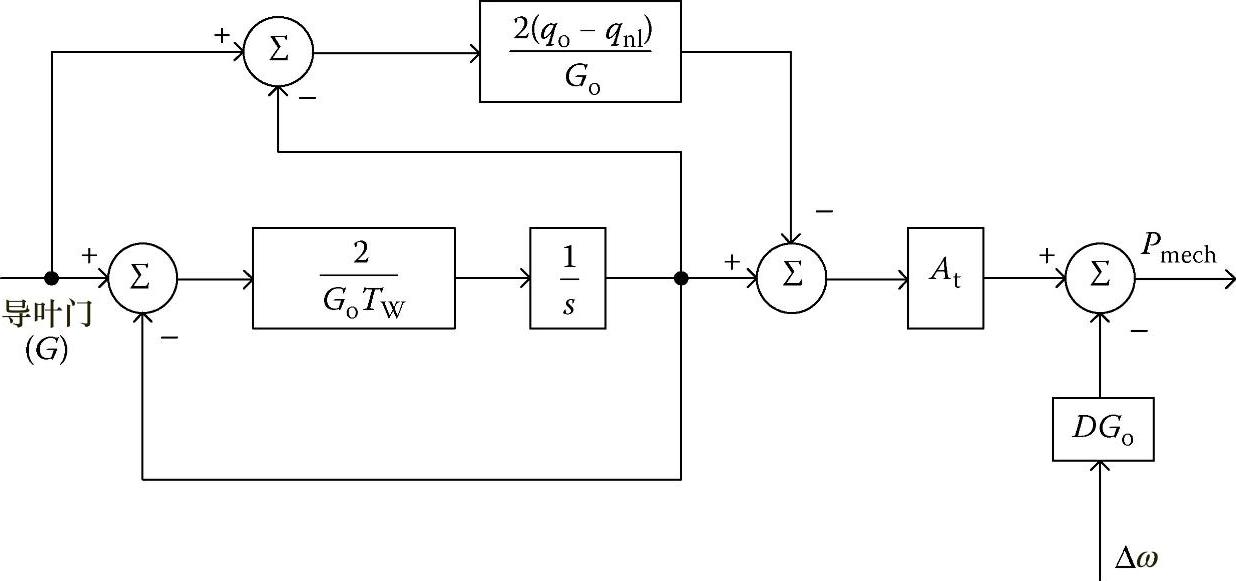
图3.25 线性水轮机模型

应当指出，导叶门开度越大，水流量也就越大。以单台机组来表征，即

式（3.12）中的阻尼项可以忽略不计，以获取常用的压力管道/水轮机线性传递函数：

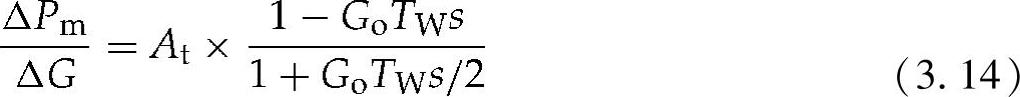
式中 G_oT_W——工作点附近的小扰动的有效水流开始时间。

考虑行波模型、调压塔影响、弹性水体状况、多种压力管道以及其他机械参数等因素，可以进一步得到详细的水轮机模型^[14-17]。不过，这里提出的模型足以供大多数分析和控制设计流程使用。