永磁同步发电机优化方案

这种发电机可用于恒速和变速应用系统。永磁同步发电机（PMSG）非常适合风力机应用，而且效率很高。

PMSG允许直接驱动（DD）式能量转换用于风能系统。直接驱动式能量转换不需要使用风力机和发电机之间的齿轮箱，因此这些系统的成本更低，而且维护工作量也小^[23，24]。不过，由风力机轴所决定的较低速度也就是发电机的运行速度。

小型永磁同步发电机的分析模型可以用等效电气方程和机械结构规格来表示。该发电机的单相绕组所感应的励磁电压的基波分量方均根值^[21，25]可以写成

式中 f——频率；

N_ph——每相匝数；

K_w1——^一次谐波绕组因数；

φ_p——由于励磁通密度分布的基本空间谐波分量而带来的每极磁通量。

每极磁通量被定义为

式中 B_lmax——励磁通密度分布的基本空间谐波分量的峰值；

l——定子铁心的有效长度；

D——定子内径；

p——极对数。

由PM产生的矩形气隙磁通密度的平值（Flat Value）B_g（当磁通密度达到最大幅值并保持不变时）与磁通密度的最大值B_lmax有关^[26]，其关系为

式中 k_f——励磁场的场形系数，该场形系数可以表示为极弧与磁极距比例的函数，该比例可由α表示：

励磁通密度分布的平值与残余磁通密度（Remnant flux density）有关。因此，PM的相对磁导率可以表示为^[23]

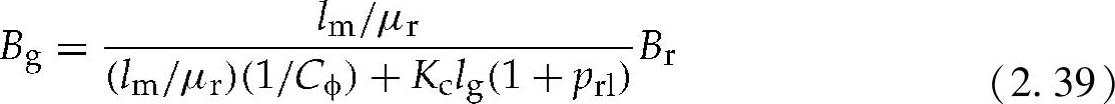
式中 l_m——PM的径向厚度；

μ_r——PM的相对磁导率；

Cϕ——磁通量聚焦因数；

K_c——卡特系数；

l_g——机械气隙；

p_rl——转子标称（normalized）漏磁导率，p_rl^一般在0.05～0.2之间

变化^[25]。

磁通量聚焦因数与发电机的具体结构有关，而且还取决于PM的径向高度^[27]。卡特系数用于补偿齿槽效应^[28]。齿槽效应是由于气隙中磁通量的减少而造成的损耗。气隙中磁通量的减弱是由于齿槽的尺寸和气隙的几何形状造成的。PM材料的相对磁导率接近一致。因此，有效气隙可视为一个常数，在转子表面安装磁体的永磁发电机里相对较大。因此，d轴和q轴的同步电抗是相同的。发电机的同步电抗等于励磁电抗X_m和漏抗X_l之和：

励磁电抗计算公式为

式中_μo——空气磁导率；

（K_cI_g+I_m/μ_r）——磁通路径上的有效气隙长度。

机械气隙是指两个磁铁之间的距离，它是由卡特系数来定义以确定PM齿槽和径向厚度的。另一方面，漏抗是定子主要漏磁通路径（如齿端、齿槽以及绕组端部漏磁通路径）磁导系数的函数^[29]：

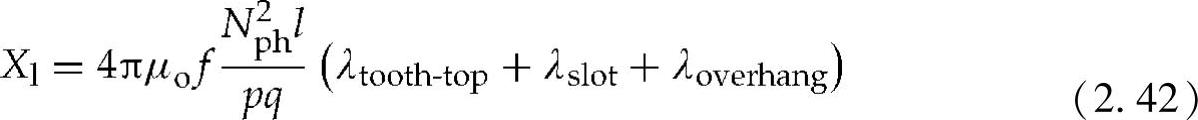
每相绕组的总长度对于其定子绕组电阻非常重要，该总长度计算公式如下：

式中l_end——定子绕组端部的长度，因此定子绕组的每相电阻可以表示为l_ph-winding：

式中 a——并联路径数；

σ_Cu——铜电导率；

A_cond——导体截面积^[23，29]。

独立的PMSG端电压可以用感应电压和由于同步电抗和发电机电阻产生的电压降来表示。对于凸极可忽略的PMSG，端电压可由式（2.45）得到^[23，29]：

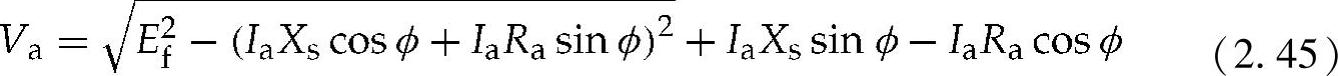
发电机输入的机械功率被转换成电功率，或者是电阻和磁损耗的形式损耗：

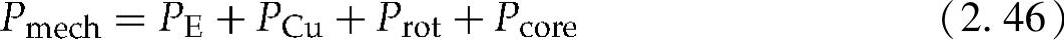
式中 P_mech——机械输入功率；

P_E——电输出功率；

P_Cu——总定子铜损；

P_rot——总旋转损耗；

P_core——发电机总铁损。

发电机的效率为

永磁发电机产生的总有功功率为

式中 V_a——电枢端电压；

I_a——电枢电流。

铜损是由于电枢电阻和电流引起的^[30]：

由于机器旋转而造成的损耗是轴承的摩擦损耗P_friction和风阻损耗P_windage的总和：

定子齿部和定子磁轭的磁滞损耗密度（分别为p_ht，p_hy）及其平均涡流损耗密度可用于近似估计发电机总磁心损耗^[30]，可写为

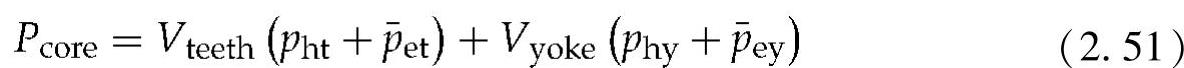
式中 V_teeth和V_yoke——定子齿部和定子磁轭的体积。(www.xing528.com)

由于d-q轴数量控制的方便性，永磁同步发电机转子的参考坐标方程可以用dq坐标表示为^[31]

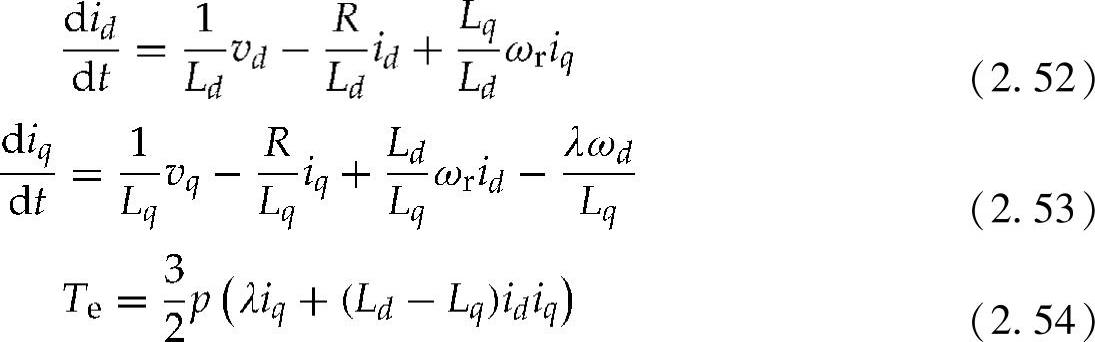
式中 L_q和L_d——q和d轴电感；

R——定子电阻；

i_q和i_d——q和d轴电流；

v_q和v_d——q和d轴电压；

ω_r——转子角速度；

λ——定子内由转子PM感应而得的磁通量幅值；

T_e——电磁转矩。

在abc坐标系下的电流和转矩方程可表示为

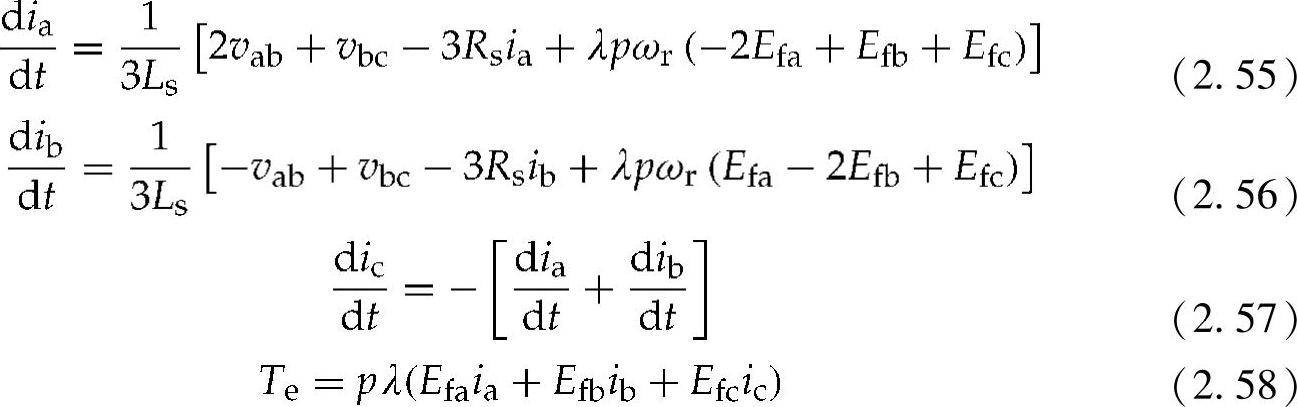
式中 L_s——定子电感；

R——定子电阻；

i_a、ib和i_c——相电流；

v_ab和v_bc——相间电压；

E_fa、Efb和Ef_c——感应电动势。

与所有电动机类似，永磁同步发电机的机械部分^[31]可以被定义为

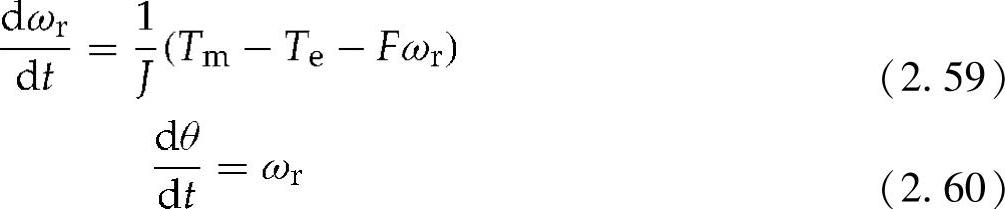
式中 J——转子和风力机的总惯量；

F——转子和风力机的总黏滞摩擦；

T_m——机械轴转矩；

θ——转子角位置。

图2.24所示为一种风力发电系统（WPS），其中PMSG与全桥整流器相连接，后接升压变换器。在本例中，升压变换器控制电磁转矩。供给侧变换器调节直流链电压并控制输入功率因数。这种配置的缺点之一是使用了二极管整流器，增加了电流幅度和损耗。此外，二极管整流导致电压下降5%～10%。电网侧变换器（GSC）可用于控制输送到电网的有功和无功功率。自动电压调节器（AVR）收集风力机转速、直流链电压、电流和电网侧电压信息，并为转换器计算出脉宽调制（PWM）模式（控制方案）。这种配置适用于小型WPS（＜50kW）^[32]。

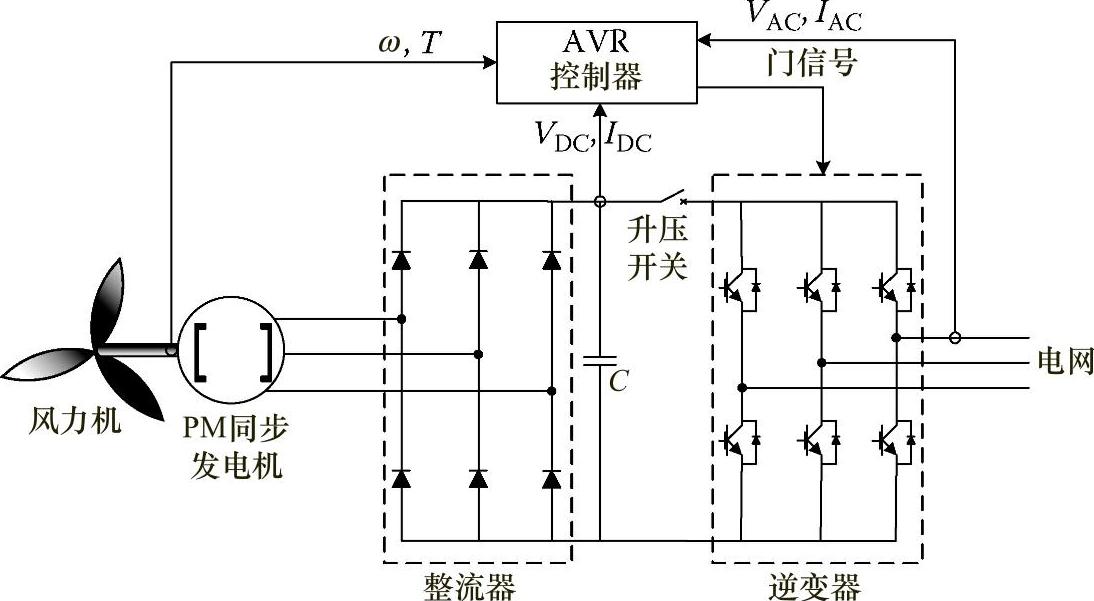
图2.24 带有整流器/逆变器的PMSG

大多数DD发电机是由同步发电机励磁。Enercon^[13]和Lagerwey等制造商使用的是同步发电机。不过Zephyros^[33]、Jeumont和Vensys等制造商使用的则是PMSG。PMSG效率更高，而且不需要任何励磁。虽然Enercon和Lagerwey早在20世纪90年代初就开始研发DD发电机，但是PM还是过于昂贵。由于在过去十年中，磁体价格下滑，许多风力机制造商开始发展配备了PMSM的DD风力机^[34]。

图2.25所示为PMSG，其中PWM整流器放置在发电机和直流链之间，PWM逆变器则连接到应用系统。在本例中，背靠背变换器可作为电网和定子绕组PMSG之间的接口^[35]。风力机可以以最高效率运行，而PMSG的变速运行则可以通过使用能够处理最大功率流的功率变换器来控制。定子端电压可以通过若干途径来控制^[36]。在这个系统中，利用磁场定向控制（FOC）来让发电机在其最佳工作点附近运行，以尽量减少在发电机和电力电子电路中的损耗。不过，其性能要取决于已知的随温度和频率而变化的发电机参数。其主要缺点是，PM的成本提升了发电机的价格，而且PM还存在去磁问题。此外，发电机的功率因数也不可调节^[14]。

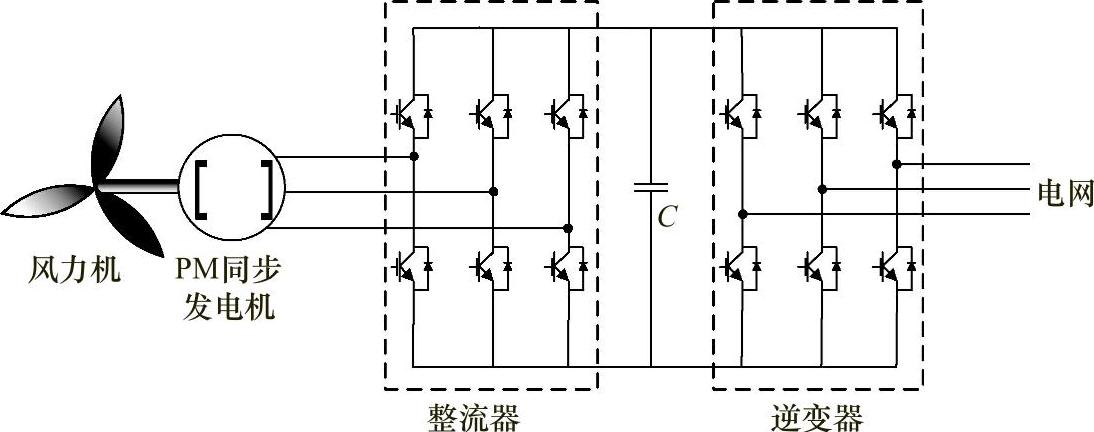
图2.25 带有背靠背逆变器的PMSG

另外，后面接有DC-DC变换器的二极管整流桥和电压源逆变器（VSI）可以用作发电机和电网之间的电力电子接口^[37]，如图2.26所示。

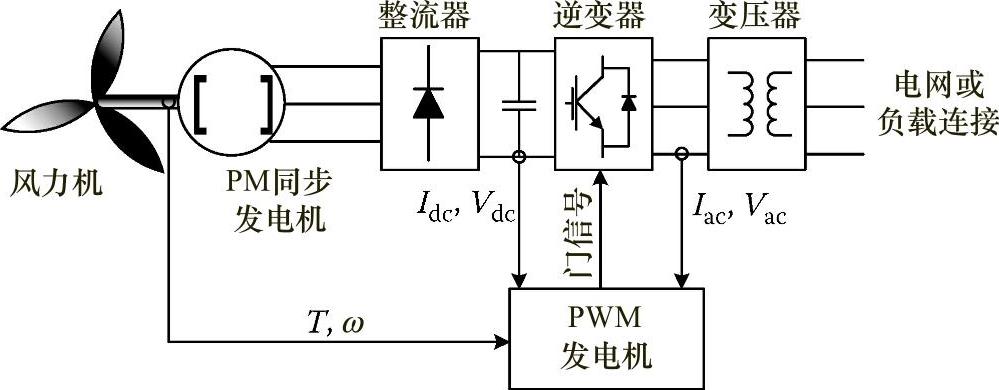
图2.26 风力机驱动的PMSG模拟框图

永磁励磁较之于电励磁的主要优点是损耗较小（无励磁损耗）和重量较轻（大约是有源发电机材料的1/2），因而成本较低。其缺点是励磁不可控。通常，永磁发电机被设计为径向磁通发电机。因此，磁铁沿径向轴励磁，但也有一些不同结构的PM例子，比如轴向磁通量和横向磁通发电机等^[38]。

轴向磁通发电机（其中磁通沿轴向磁轴）比径向磁通发电机体积要小，但它更重而且也更贵^[15]。这主要是由于轴向磁通发电机的力场强度，并不是对于所有的半径都是最优的，力场作用的半径也不全都是最优的。

由于横向磁场发电机（在一个极对的横向的不同极性相对的PM^[39]）的力场强度很高^[32]，在风力机中使用这种发电机已经非常普及。这些机器的主要问题是存在较大的气隙，从而弱化了这种高力场强度。横向磁场发电机的优点是定子绕组几何形状简单，为使用高电压绝缘提供了可能性。其缺点是功率因数非常低，而且结构复杂，这可能会导致机械故障和音频噪声。

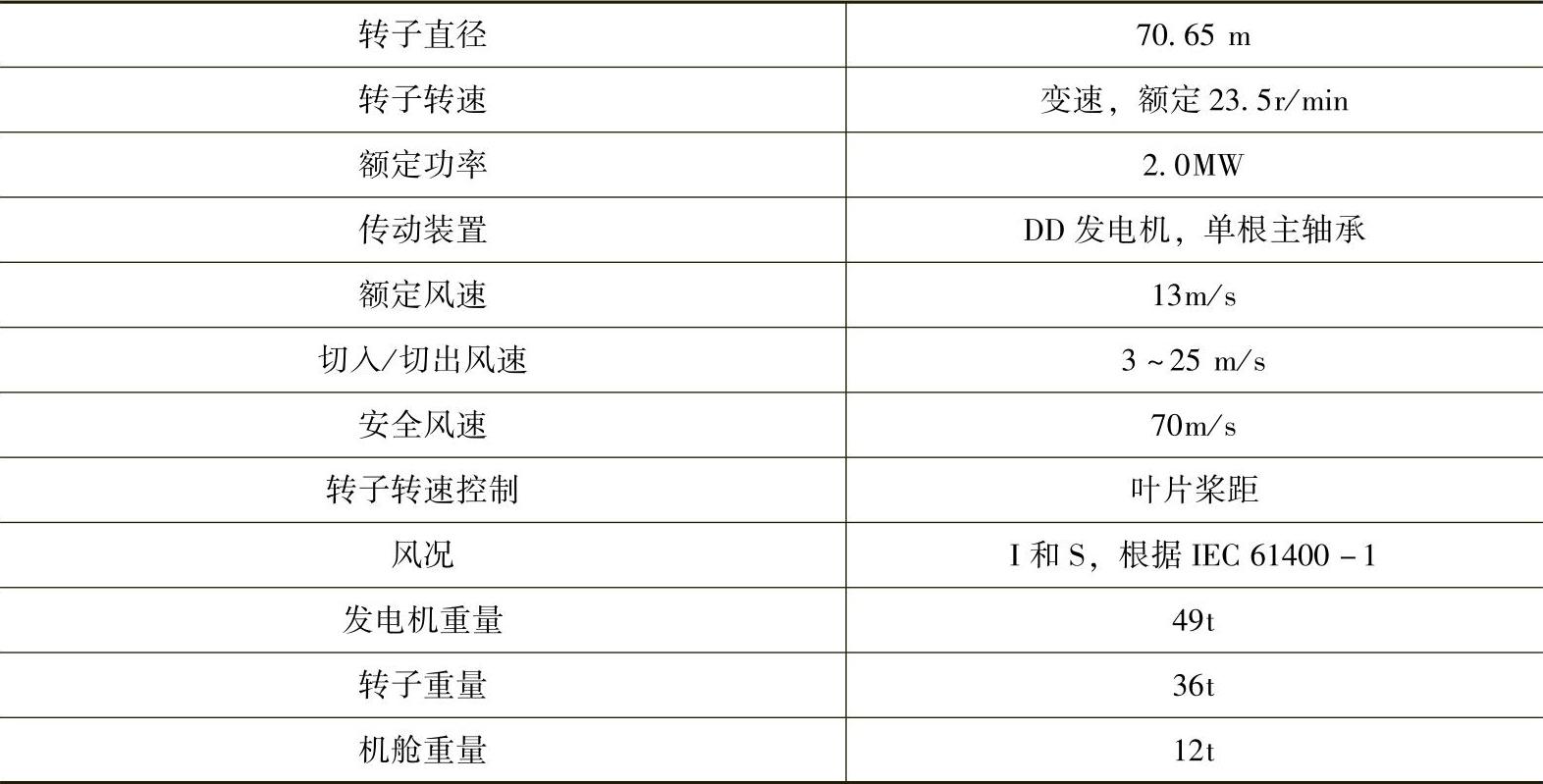
Zephyros是一款带有PMSG的商业化风力机，其技术规格见表2.5^[33]。

表2.5 Zephyros风力机技术规格

Zephyros风力机的风速与输出功率曲线关系如图2.27所示^[33]。

风力机产生驱动PMSG的机械转矩。这种应用没有使用桨距角控制器，而且桨距角保持在10°不变。作为风力机的输入，风速保持在10m/s不变。PMSG是一款300V_dc、2300r/min的发电机，额定基本转矩为10N·m，最大转矩为14.2N·m。其电气参数如下：

定子电阻：R_s=0.4578Ω。

轴电感：L_d=3.34mH，L_q=3.34mH。

磁铁感应的磁通量：λ=0.171Wb。

发电机的机械参数如下：

转动惯量：J=0.001469kg·m²。

摩擦系数：F=0.0003035N·ms。

极对数：p=4。

对发电机转子的速度记录1s，如图2.28所示。根据图2.28可以看出，在给定的条件下，转速高于同步速度。

图2.29所示为风力机产生的机械转矩，它是PMSG的输入转矩。应当指出，仿真最初期的转矩瞬态响应是由时间零点处的涡轮动力学特性和发电机的失速工况引起的。随着转矩的增大，发电机的转速也在增大，并在转矩稳定时达到稳态工况。风力机产生的机械转矩，即PMSG的输入转矩，如图2.29所示。应该指出的是，仿真刚开始时，转矩的瞬态响应取决于涡轮动力学以及时间零点的发电机失速状态。随着转矩增大，发电机的转速也在增大，并在转矩固定时达到稳态工况。

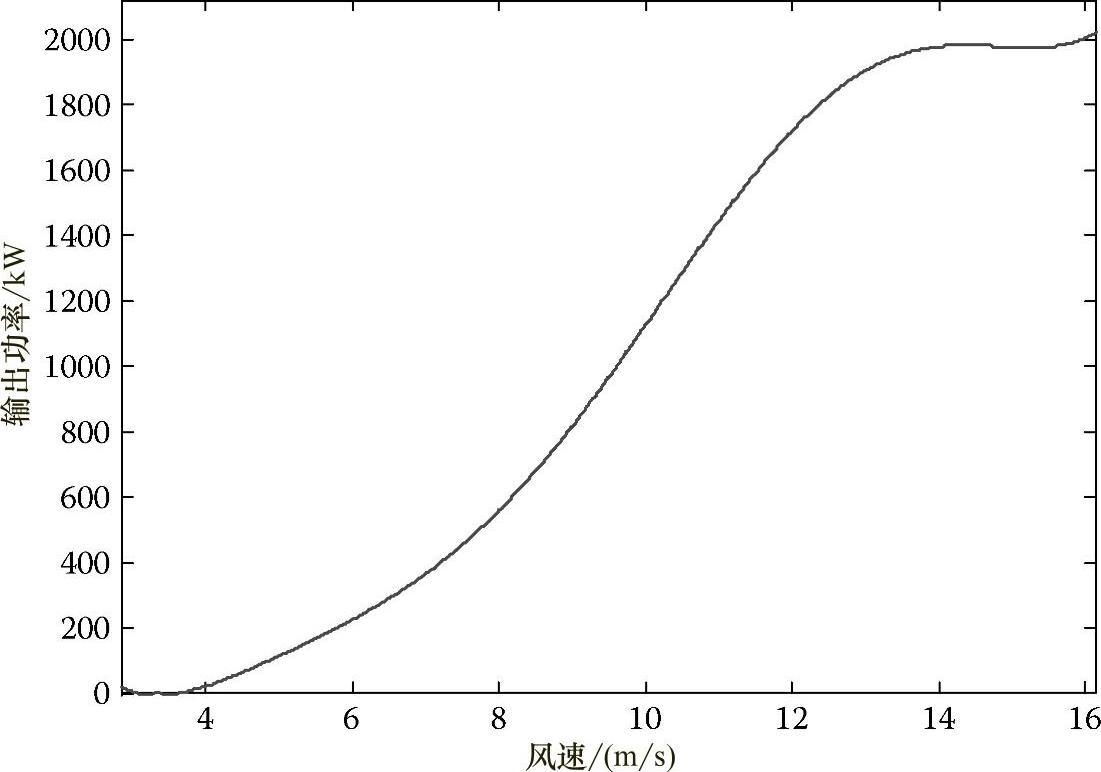
图2.27　Zephyros风力机的风速与输出功率曲线关系图

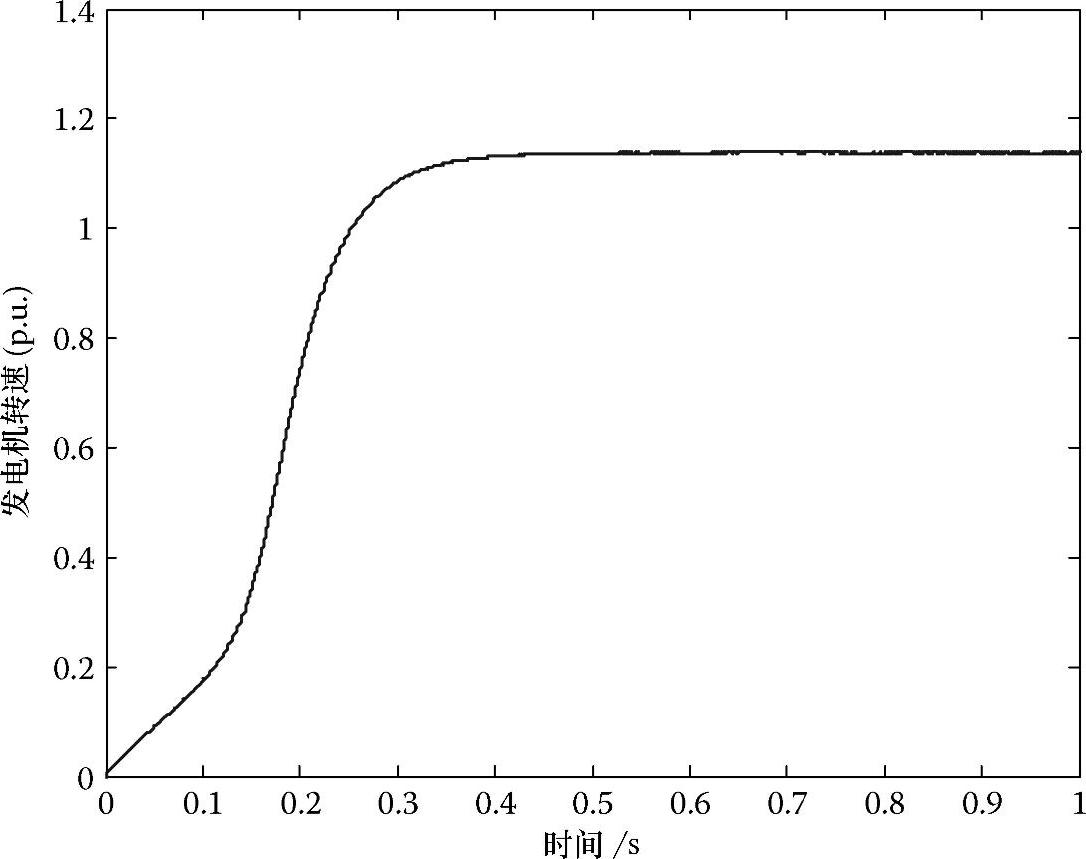
图2.28　PMSG的转子转速

PMSG端电压整流如图2.30所示。直流母线电容器端测量到的直流母线电压如图2.30所示。直流母线电压在瞬态工况后达到稳态值，并且在运行期间保持恒定。

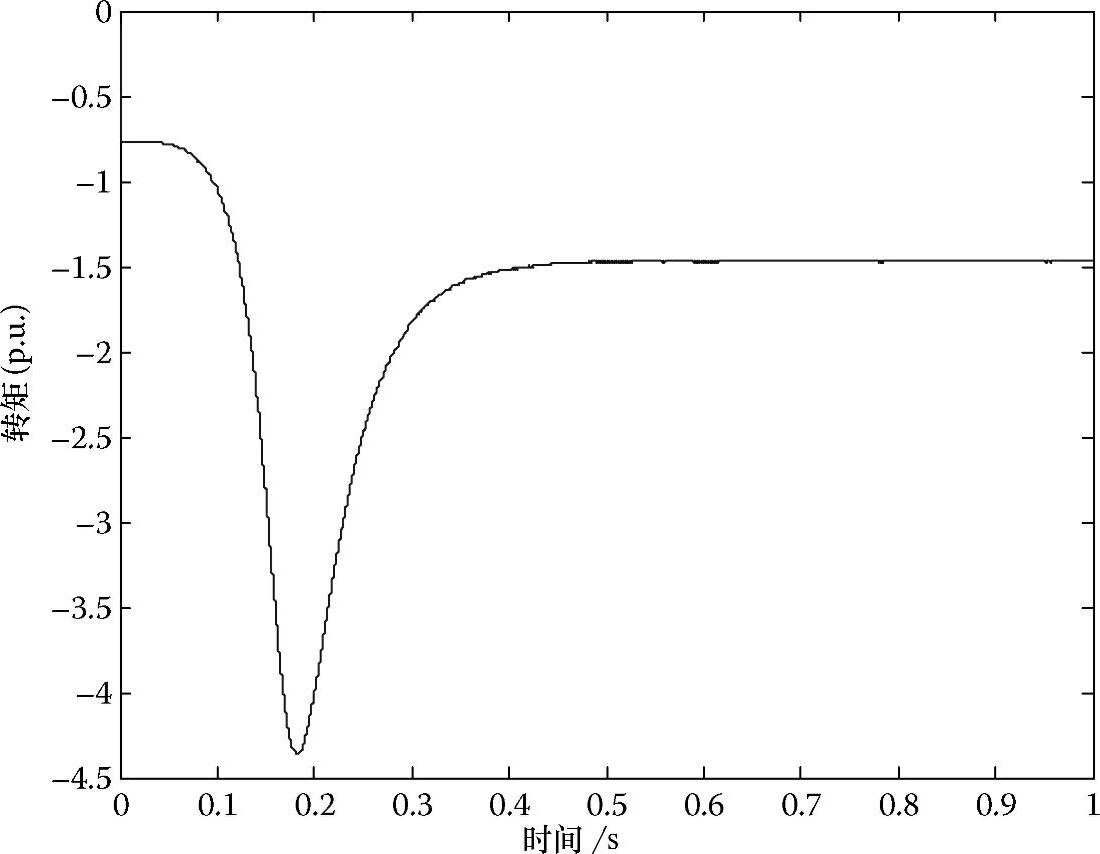
图2.29 直接驱动PMSG的转矩

逆变器中的第一个开关的端子电压测量值如图2.31所示，这是PWM斩波式直流母线电压。

DC-AC逆变器的输出和变压器之后的线间电压如图2.32所示，这是一个可以支持交流负载的PWM正弦电压。

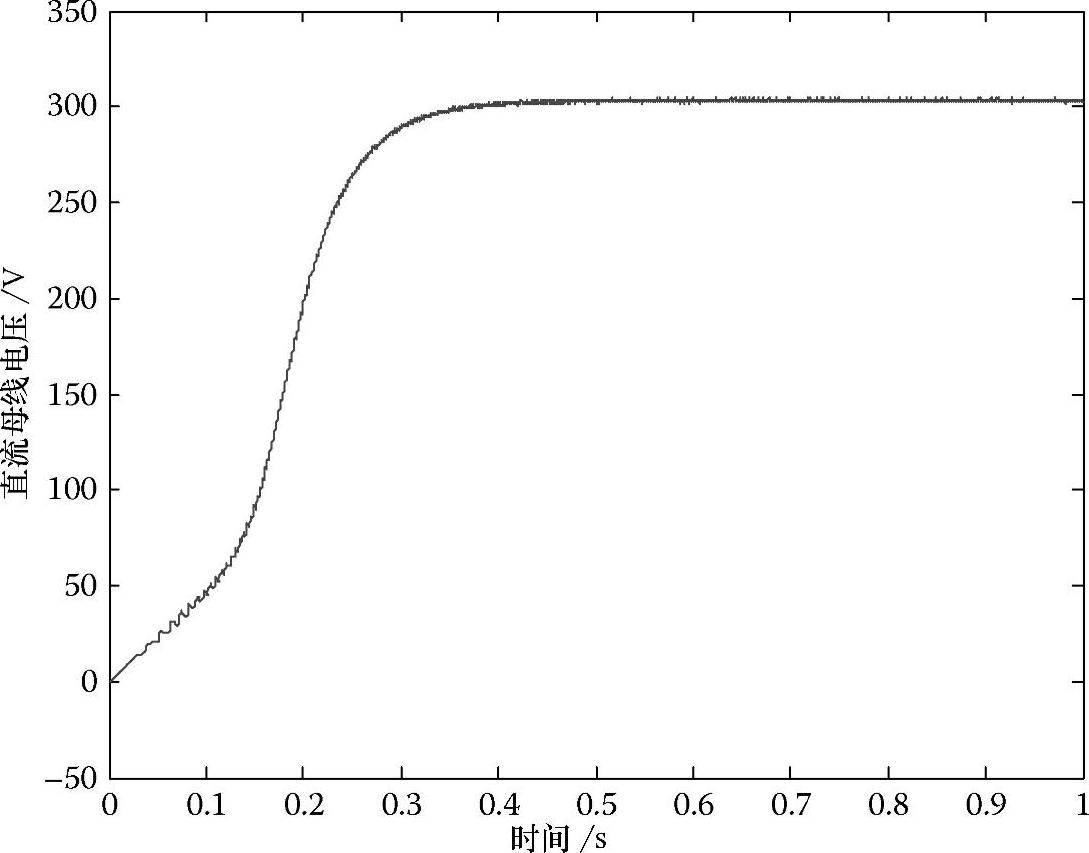
图2.30 整流器的输出电压

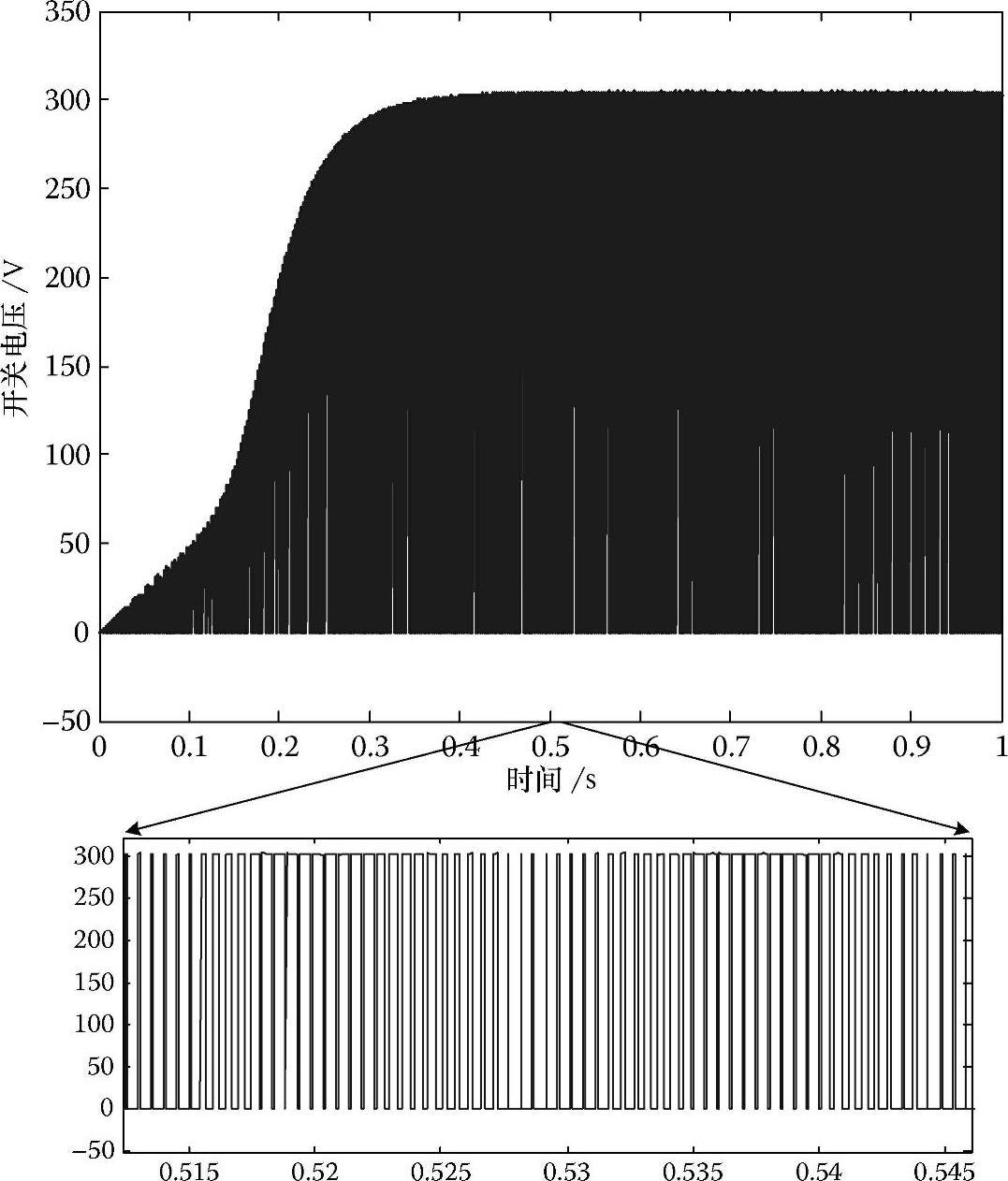
图2.31 逆变器的第一个开关电压