光伏电池遮蔽效应的解析，

当一个光伏阵列或者它的一部分由于遮蔽物的影响而产生不完全辐照时，就会出现遮蔽效应。在光伏组件被部分遮蔽时，它的一些电池能够以反向偏压方式工作，此时它是作为负载而不是发电器。如果反向偏压超过被遮蔽的太阳电池的击穿电压，它可以作为一个开路，并将整个光伏组串损坏^{[31，74，75]}。

为了减少遮蔽的影响，大多数商用光伏组件都含有内部旁路二极管。不过光伏组件中二极管数远远低于串联在组件中的电池数^[31]，因此降低了开路风险。但是，光伏组件总功率输出量也相应降低了，因为当一个旁路二极管导通时，很多太阳电池就出现了故障。

图1.33显示了两个光伏阵列。在第一个阵列中，每个光伏电池都并联有自己的旁路二极管。

与图1.33所示的第二种结构相比，第一种结构更能够抵抗遮蔽带来的负面影响，而且还可以产生更多的功率。当一个阵列受局部遮蔽所限，第二种结构中的电池串就会出现故障，而在第一种结构中，只有受影响的电池才会出现故障。

图1.34所示为完全辐照的阵列以及图1.33中描述的两种不同结构的阵列的I-V曲线。

图1.33 与每个电池连接的旁路二极管和与整个电池串连接的旁路二极管

a）与每个电池连接的旁路二极管 b）与整个电池串连接的旁路二极管

图1.34 遮蔽工况下的光伏串I-V特性

为了计算遮蔽效应，可以引入遮蔽因子（S）^[75]：

式中 A_S——遮蔽面积；

A_C——光伏组件的总面积；

E——无遮蔽电池E₀上的平均辐照水平。

在不同遮蔽因子下的光伏电池I-V曲线就像图1.35中给出的不同辐照度条件下的光伏电池一样。

图1.35 不同遮蔽因子下的I-V特性

此外，在遮蔽工况下，P-V曲线也会受到影响。当发生局部遮蔽时，两个不同的电压值就会存在两个不同的功率峰值，如图1.36所示。

图1.36 在遮蔽条件下的MPP重定位

许多MPPT方法会跟踪局部峰值，因此可能无法找到全局峰值。这在局部遮蔽工况下可能会非常重要。因此，在计算MPP时应该考虑遮蔽效应。

遮蔽效应可以包括在没有电阻的单二极管模型中。2.3.3节^[2]中描述单二极管模型的式（1.48）可以修改为描述一个单电池的公式：

其中，光电流（I_PH）与太阳辐照度具有线性关系，而短路电流（I_SC）则与I_PH相等^[75]。这一线性关系对于遮蔽效应（S）同样有效：

式中 I_SC0——全辐照的电池的短路电流。

对于I=0，式（1.48）可以改写为

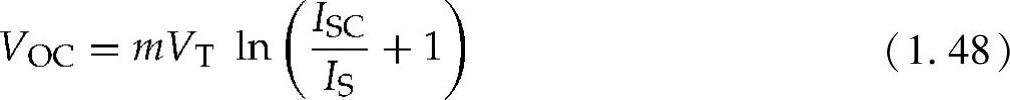
因此，V_OC可以写为

无遮蔽电池的开路电压为

遮蔽问题影响到光伏组件的MPP，因此MPP处的电流和电压关系可以写成

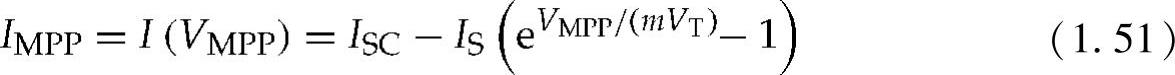
通过对式（1.53）进行求导，可以求得MPP处的电压为

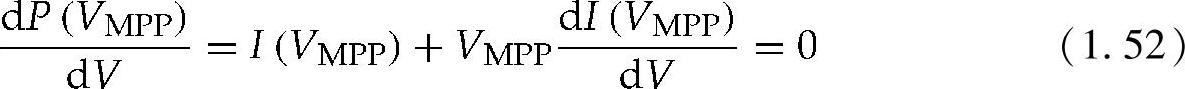
可得(www.xing528.com)

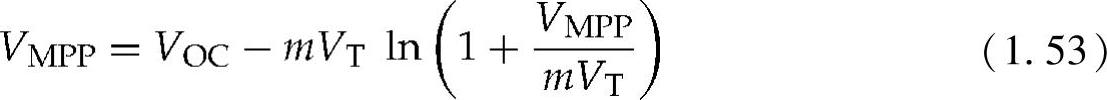
式（1.55）中的非线性方程可以将对数部分使用泰勒级数展开来近似表示为

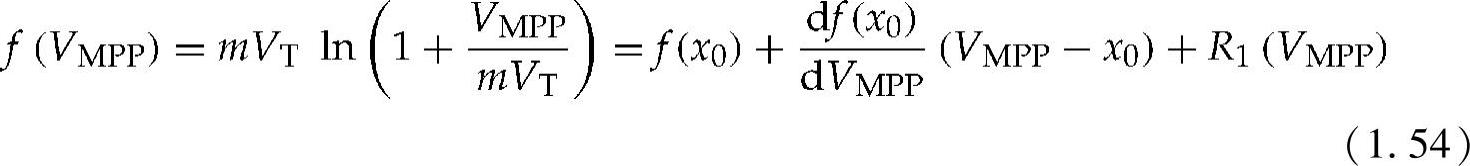
代表与高阶导数相关项的R₁（V_MPP）可以忽略不计。对于泰勒级数逼近点V_MPP，定义x₀=cmV_T（c为常数）可得

当c在[10，1000]取值时，线性化函数可以看作原函数的精确逼近^[75]。因此，其显式解为

常数c₁和c₂可以表示为

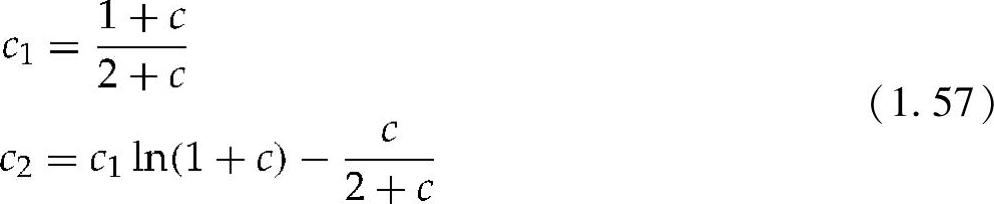
MPP处的电压可使用下式求得：

那么，作为遮蔽因子函数的MPP电压变为

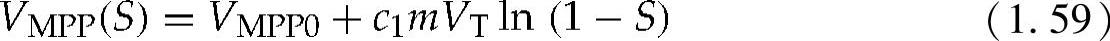
在c取较高值时，可以假设c₁≈1，I_SC0＞＞I_S，而且

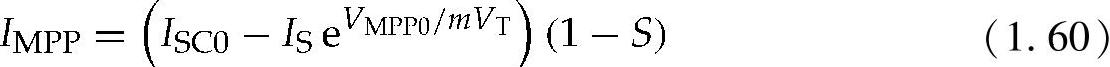
令I_MPP0=I_SC0-I_SeV_MPP0/（mV_T），MPP处的电流（I_MPP）作为S的函数将变为

在没有任何遮蔽的情况下，填充因子可以被描述为

在遮蔽工况下，可以将一个新的填充因子定义为S的函数，即

其中，常数c₃和c₄为I_SC0的函数，有

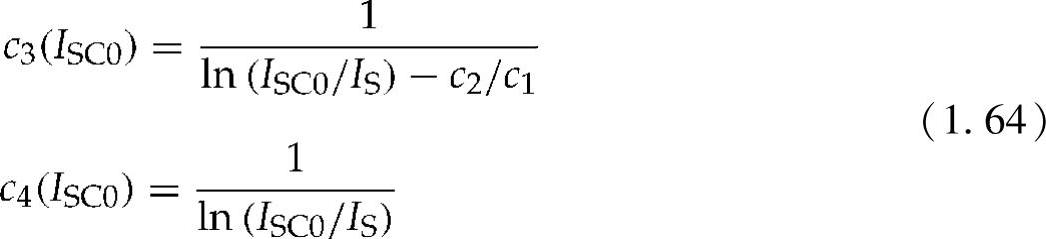
使用最大功率，P_MPP0=V_MPP0I_MPP0，而且在遮蔽工况下的MPPc₃可写为

太阳电池的效率也会受到遮蔽效应的影响。该效率可以使用下式来计算：

式中 A_C——电池的总面积；

E——平均辐照度。

式（1.68）中的P_MPP可以换成式（1.69），并使用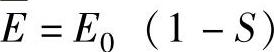，总效率公

式为η₀=P_MPP0/（A_SE₀）作为遮蔽因子的函数，变为

式中E₀——无遮蔽电池的辐照度；

A_S——遮蔽面积。

图1.37给出了MPP、填充因子以及不同遮蔽因子下的效率。因为遮蔽因子大于特定值，因此其效率和填充因子会突然下降。遮蔽的光伏电池的功率特性几乎随着遮蔽因子的增大而呈线性下降^[75]。

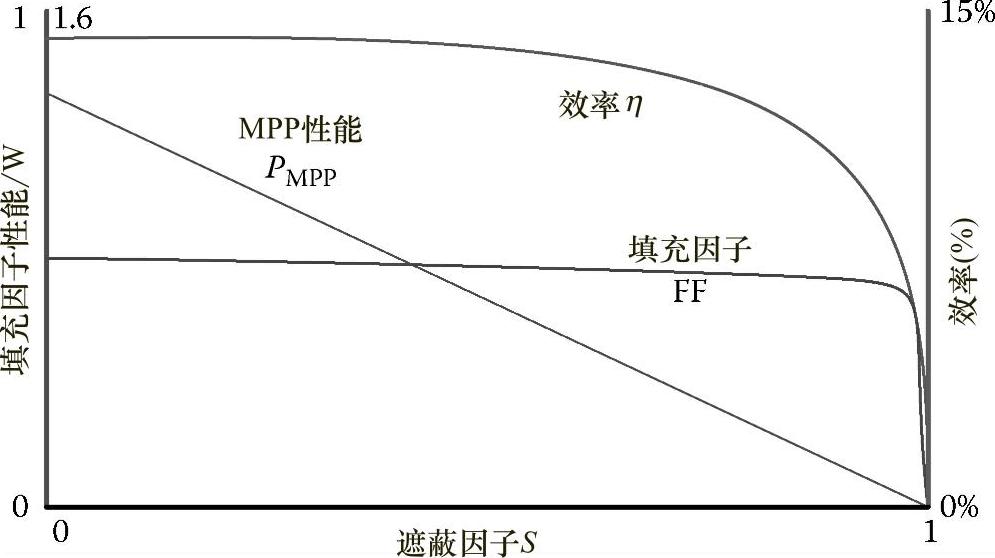
图1.37 P_MPP、FF和η随遮蔽因子S的变化