光伏电池模糊逻辑控制的MPPT优化方案

随着微控制器和DSP技术的发展，模糊逻辑控制^[49-58]已经在MPPT应用领域引起广泛兴趣。参考文献^[57]指出，模糊逻辑控制器对于非线性系统来说很有优势，它不需要精确的动态模型，而且还可以处理不精确的输入。

模糊逻辑控制根据三个阶段。模糊化阶段根据图1.26所示的隶属函数，将输入变量转换成语言变量。这个例子中有五个模糊等级，分别为NB（负大）、NS（负小）、ZE（零）、PS（正小）和PB（正大）。为了提高精度，可以使用更多的模糊等级。a和b是以图1.26中数值变量的取值范围为基础的。在隶属函数中，可以将某些指定的模糊等级设计为不对称状态，使它们更占优势，换句话说，给它们赋予更高的重要程度^{[49，53，57，58]}。

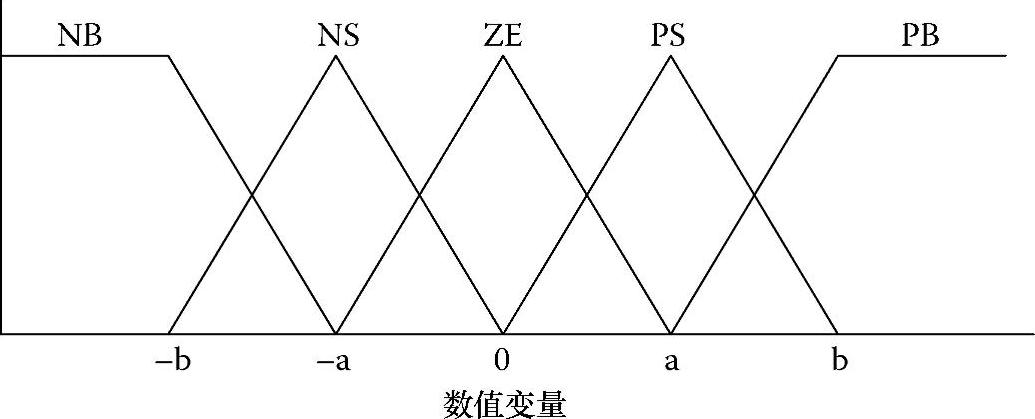
图1.26 模糊逻辑控制器输入和输出的隶属函数

误差E及其变化ΔE是基于模糊逻辑的MPPT控制器的输入。E和ΔE可以根据用户的偏好而计算得到。由于dP/dV在MPP处更接近于零，因此可以使用近似的式（1.34）^[59]：

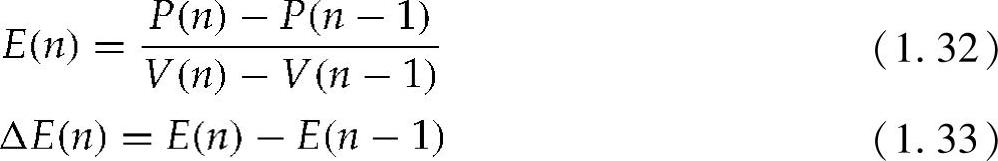
另外，误差信号可以根据下式求得：

式（1.35）^[1]中的误差变化也可以应用到式（1.36）中。式（1.36）中的误差是瞬时电导和增量电导之和，在接近MPP时为零。一般来说，模糊逻辑控制器的输出是电力变换器占空比ΔD的变化。占空比的这种变化可以在类似于表1.3的一个查找表中查找^[50]，之后计算E和ΔE，并转换成语言变量。(www.xing528.com)

误差E及其变化ΔE的不同组合可作为分配给ΔD的语言变量。对于升压变换器来说，表1.3就可以用于这一目的。例如，如果工作点远离MPP右侧，E为NB，且ΔE为ZE，占空比就需要幅度更大一些的下降，以降低电压，也就是说，ΔD应该为NB，以达到MPP。

表1.3 模糊规则库

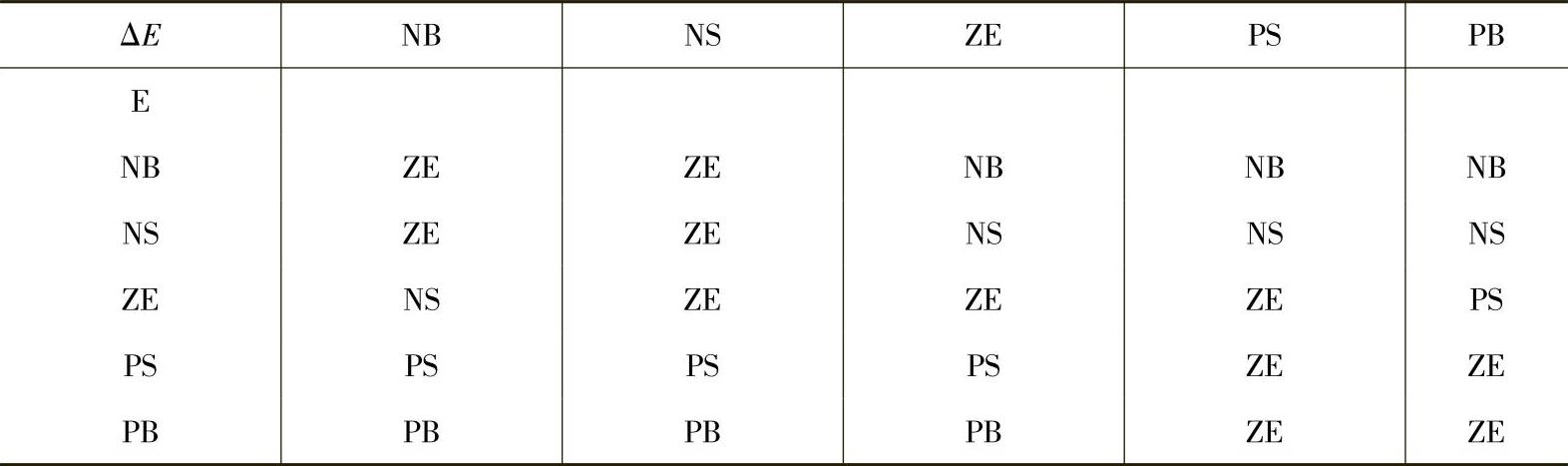
在去模糊化阶段，模糊逻辑控制器的输出使用图1.27所示的隶属函数，从一种语言变量转换成数字变量。通过去模糊化，控制器产生一个模拟输出信号，该信号可以被转换成数字信号，并控制MPPT系统的电力变换器。

图1.27所示为基于模糊逻辑控制器的MPPT的实现示例。测量电压和功率来计算式（1.34）和式（1.35）中的E和ΔE，然后使用类似于表1.3的一个模糊规则库表来评估这些值。模糊规则库表的输出就是在占空比中所需的改变。在去模糊化阶段，占空比的数值通过语言值的转换来确定。最后，通过一个模拟-数字（A-D）转换器和栅极驱动器，将必需的开关信号施加到MPPT的电力变换器上。

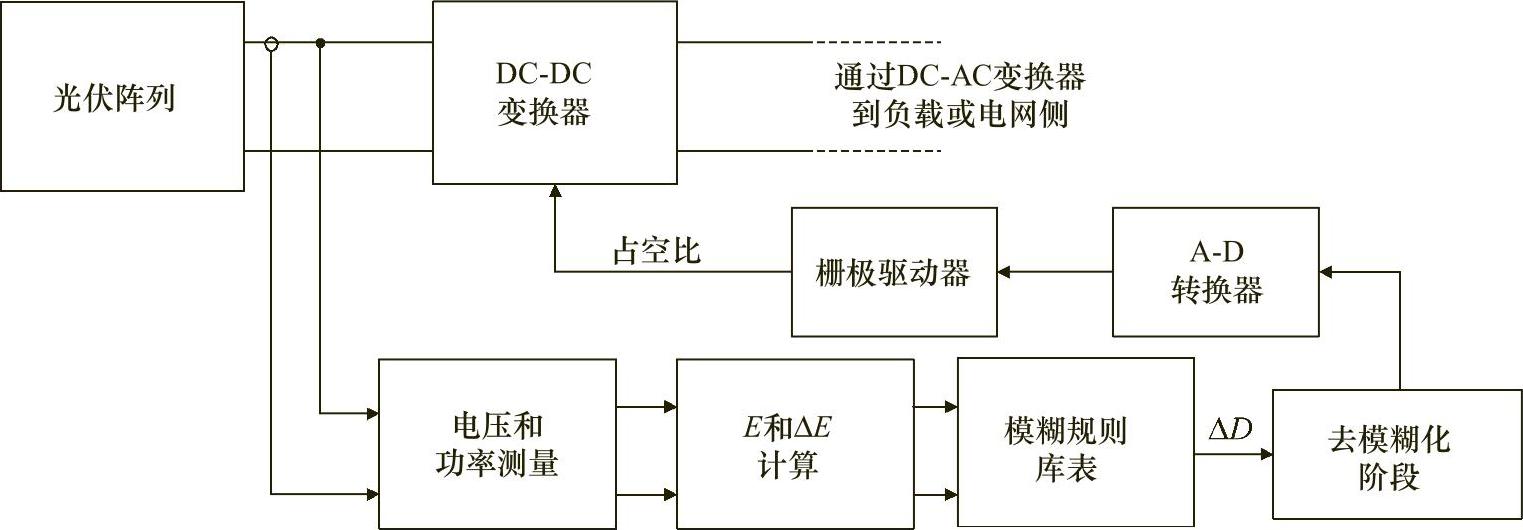
图1.27 基于模糊逻辑控制器的MPPT实现

在不同的大气条件下，模糊逻辑控制器均能在MPPT应用中表现出良好的性能。另一方面，模糊逻辑控制器的有效性取决于误差及其变化的计算和用户开发的规则库表的准确性。为了获得更高的效率，隶属函数和规则库表可以不断更新或者调整，以达到类似于自适应模糊逻辑控制器的最佳性能^[55]。通过这种方式，可以实现MPP的快速收敛，以及在MPP周围的最小波动^[52]。此外，跟踪性能取决于隶属函数的类型^[57]。