单个相移单元中驱动电压与相移量之间的关系定量化

液晶盒是液晶光学相控阵单个相移单元的物理模型，其基本结构如图4.1所示。液晶盒一般分为7层：上下两玻璃基板层，上下两电极层，上下两取向膜层以及中间的液晶层。在以下的计算中，将考虑取向膜的厚度及其对指向矢分布的影响。

图4.1　液晶盒的基本结构

液晶指向矢的计算是分析液晶器件电压－相移特性的前提和基础。在目前采用的计算方法中，牛顿法仅适用于求解最简单的液晶盒；模拟退火法虽然能得到全局最优解，但求解速度非常慢；有限元法比较通用，但是它更适合于大型软件；目前比较通行的方法是张弛法，也有人采用有限差分法，最近又有人提出了比较适用的差分迭代法。

向列型液晶是一种介于液体和晶体两种状态的物质，一般分子形状呈长棒形，具有光学各向异性。在电场作用下，液晶分子的排列会发生相应的变化，从而引起液晶光学性质的变化。液晶的这种电光效应，是各种液晶光学器件工作机制的物理基础。液晶盒结构的数学建模、液晶指向矢的准确计算以及液晶的电压－相移特性的研究，是分析和设计液晶光学器件的基础。

目前，液晶盒的数学模型一般没有考虑取向膜的厚度。在液晶光学器件中，比较精确的电压－相移特性是准确分析液晶对光波的相位调制作用的基础和关键，因此本章考虑了取向膜的厚度。液晶光学相阵列的相位延迟单元是通过液晶对光波的相位调制作用来实现的，因此，在液晶光学相阵列的设计中最基础的工作就是研究一维液晶盒的电压－相移特性。

根据液晶连续体弹性形变理论，液晶盒内的Gibbs自由能密度为

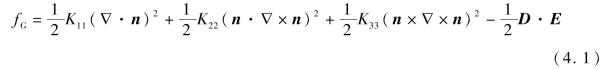
式中，n＝（nx，ny，nz）为指向矢；K11，K22，K33分别为展曲、扭曲和弯曲弹性系数；D，E分别为电位移矢量和电场矢量，且有D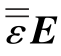＝，E＝－∇φ，φ为电位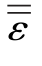，为液晶的介电张量，表示为εij＝ε⊥δij＋Δεninj，Δε＝ε／／－ε⊥。

一维情况下，，Gibbs自由能密度具体表达式为

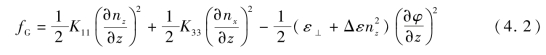
于是液晶盒内总的Gibbs自由能为

液晶在外电场作用下达到平衡状态时，其Gibbs自由能趋向最小值。应用变分原理，可以得到关于指向矢和电位的Euler－Lagrange方程组：

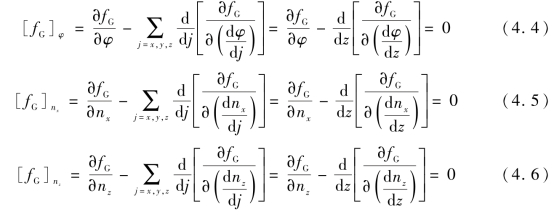
以上是一组偏微分方程，求解的方法有松弛法、牛顿法、差分迭代法或其他迭代法等，本章提出一种新的混合方法。(www.xing528.com)

选取液晶材料E7（Merck公司）为例，其参数为K11＝11.1×10－12N，K22＝7.4×10－12N，K33＝17.1×10－12N，ε／／＝19.0，ε⊥＝5.2。上下两取向膜的厚度均取为d_film1＝d_film2＝0.1μm，介电常数取为εf＝3.0，液晶盒厚度取L＝5μm，上下两个预倾角分别取为θ01＝10°和θ02＝2°。采用本章提出的混合算法，可以计算得到液晶盒中指向矢的分布，如图4.2所示。

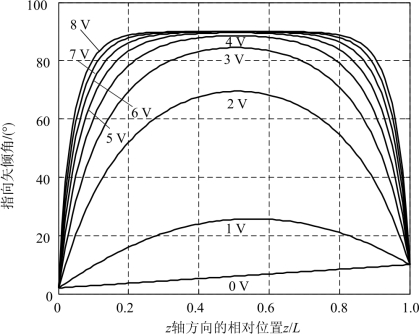
图4.2　液晶盒中指向矢的分布

把液晶看作单轴晶体，由指向矢的分布计算得到液晶盒的等效折射率：

其中，ne（z）为液晶中非寻常光的折射率分布，表示为

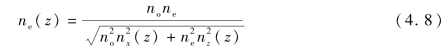
通过计算，液晶的等效折射率随电压变化的曲线如图4.3所示。

于是，液晶中光波的相位延迟量为

为了表示液晶对光波的相位调制作用，以没有施加电压时液晶对光波的相位延迟量为基准，加上不同电压后的相位延迟与它相比较，得到一组相对相移量，这就是需要的电压－相移曲线，如图4.4所示。这是液晶相位调制器件工作的基础。

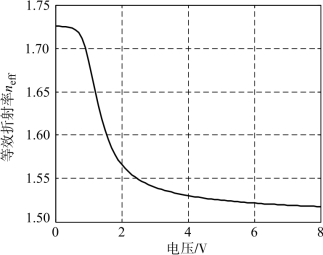
图4.3　液晶的等效折射率

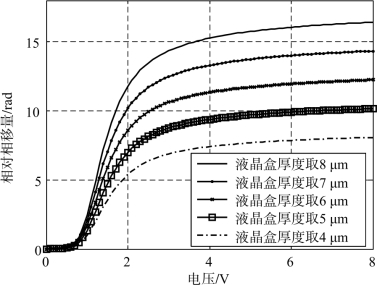
图4.4　液晶相移单元的电压－相移特性（取不同液晶盒厚度）