虽然菲涅耳给出了光的衍射的复振幅的具体数学模型表达式,但是其仍然存在很多不足,只能体现出衍射场复振幅与相位的贡献关系,其他参数项也只是体现了其中的物理逻辑关系,并没有给出具体的数学关系表达式,仍然不能用于实际衍射远场的光强分布特性分析和计算,而且其在角度为π/2的倾斜因子K(θ)数值的假设也是不正确的。所以,惠更斯-菲涅耳原理从严格理论分析上来说,还是不完善的,还需要深入的分析和理论突破。
基尔霍夫(Kirchhoff)受到惠更斯-菲涅耳原理的启发,他认为如果把所有问题都考虑进来解释光的衍射现象,要得到具体的数学物理表达式是不切实际的,而且也是不必要的。由于电场和磁场的特定相互关系,他认为只考虑光传播过程中的磁场或者电场中的一个横向分量,在分析光的衍射时,把光波作为一个标量来处理似乎是可行的。虽然基尔霍夫的这种处理方法忽略了电场和磁场直接的耦合关系所带来的影响,但后期的实验证明,在一定的条件下该理论思想很符合实验测试结果。
惠更斯-菲涅耳数学公式理论上适应任何形状的波阵面或衍射屏和衍射小孔,但是实际运用中,这种二元积分的计算是非常复杂和困难的,必须简化数学公式以获得衍射远场的分布特性。基于电磁场理论的边界条件和数学理论中的格林定理,基尔霍夫认为球面波标量的光衍射公式进一步深入细化,如图3.16所示的开孔Σ的衍射远场P点的复振幅就可从式(3.2)演变为相同形式的公式:式中,n为开孔Σ某一点Q位置的波阵面法线方向;r为P、Q两点的直线距离;l为开孔Σ处Q点和点光源S之间的直线距离。式(3.35)被称为基尔霍夫衍射公式,相对式(3.34)有了很大的进步和完善。(https://www.xing528.com)
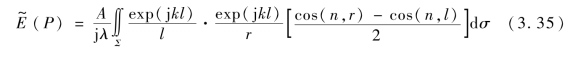
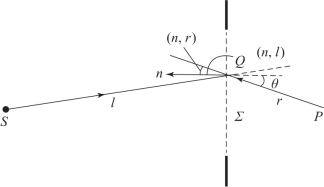
图3.16 球面波在开孔Σ上的衍射
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




