本节依次讲解6种基本斩波电路,并重点阐释降压斩波电路和升压斩波电路的工作原理。
5.1.1 降压(Buck)斩波电路
图5-1(a)点划线框内全控型开关管V和续流二极管VD构成了一个最基本的开关型直流-直流降压变换电路。这种降压变换电路连同其输出滤波电路LC被称为Buck型DC/DC变换器。对开关管V进行周期性的通、断控制,能将直流电源的输入电压E变换为电压ou输出给负载。
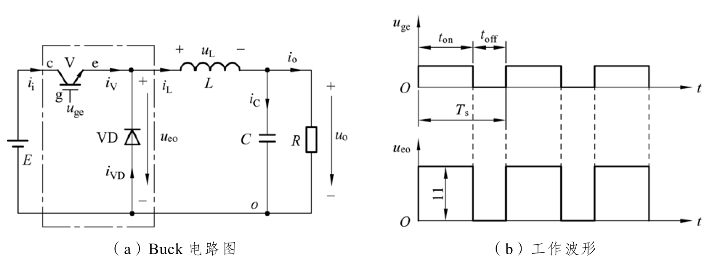
图5-1 Buck变换器
1)理想的电力电子变换器
为了获得各类开关型变换器的基本工作特性而又能简化分析,在本书各章的分析中除特意研究开关管开通、关断过渡过程而特别指明外,都假定电力电子变换器是理想的,理想条件是:
(1)开关管V和二极管VD从导通变为关断,或从关断变为导通的过渡过程时间均为零,且通态压降为零,断态漏电流为零。
(2)在一个开关周期中,输入电压E保持不变;输出滤波电容电压uo有很小的纹波,在分析开关电路变换特性时,可认为ou保持恒定不变,其值为输出的直流电压平均值Uo。
(3)电感和电容均为无损耗的理想储能元件。
(4)线路阻抗为零。电源输出到变换器的功率等于变换器的输出功率,即 EIi =UoIo 。
2)降压原理
在一个开关周期Ts期间对开关管V施加如图5-1(b)所示的驱动信号uge,在ton阶段,uge > 0,开关管V处于通态,在toff阶段,uge<0,开关管V处于断态。对开关管V进行高频周期性的通、断控制,开关周期为Ts,开关频率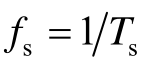 。开关管V导通时间ton与周期Ts之比称为开关管导通占空比D,简称导通比或占空比,
。开关管V导通时间ton与周期Ts之比称为开关管导通占空比D,简称导通比或占空比,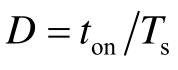 。在开关管V导通期间,直流电源E经开关管V直接输出,电压ueo=E,这时二极管VD承受反压而关断,iVD=0,电源电流ii经开关管V流入电感负载,电感电流iL =ii 上升。在开关管截止期间,负载与直流电源脱离,由于电感电流iL不能突变,电感电流iL经负载和二极管VD续流,电感电流iL =iVD下降。如果在开关管V整个关断期间,电感电流iL并未衰减到零,即在整个周期Ts中iL>0,称为电流连续,则变换器的输出电压ueo=0。
。在开关管V导通期间,直流电源E经开关管V直接输出,电压ueo=E,这时二极管VD承受反压而关断,iVD=0,电源电流ii经开关管V流入电感负载,电感电流iL =ii 上升。在开关管截止期间,负载与直流电源脱离,由于电感电流iL不能突变,电感电流iL经负载和二极管VD续流,电感电流iL =iVD下降。如果在开关管V整个关断期间,电感电流iL并未衰减到零,即在整个周期Ts中iL>0,称为电流连续,则变换器的输出电压ueo=0。
由图5-1(b)可得,在电流连续的工作情况下,变换器输出电压ueo平均值为
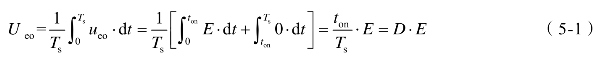
由电路原理可知,当电路处于稳态的情况下,电感两端电压的平均值为零。因此负载上电压的平均值Uo等于变换器输出电压平均值Ueo,即

3)控制方式
由式(5-2)可知,Buck电路有3种方式调节或控制输出电压平均值Uo:
(1)保持开关周期Ts恒定不变,通过调节导通时间ton而改变平均输出电压,此种方式称为脉冲宽度调制(PWM);
(2)保持导通时间ton恒定不变,通过调节开关周期Ts而改变平均输出电压,此种方式称为频率调制(PFM);
(3)同时调节开关周期Ts和导通时间ton,从而改变平均输出电压,此种方式称为混合调制。
为应用方便,一般采用第一种方式。
1.Buck变换器电感电流连续时工作特性
Buck变换器有两种可能的运行工况:电感电流连续模式CCM(Continuous Current Mode)和电感电流断续模式DCM(Discontinuous Current Mode)。电感电流连续是指图5-2(a)中输出电感L的电流在整个开关周期Ts中都存在。电感电流断续是指在开关管V关断的toff期间后期一段时间内输出电感的电流已降为零。处于这两种工作情况的临界点称为电感电流临界连续状态,这时在开关管关断期结束时,电感电流刚好降为零。图5-2(e)、(f)分别给出了电感电流连续和断续两种工作情况时的电压、电流波形图。本节分析电感电流连续时Buck变换器的工作特性。
1)两种开关状态
图5-2(a)中在一个开关周期Ts的ton期间,开关管V处于导通、二极管VD处于关断状态,定义为开关状态1;在toff期间,V关断、VD导通定义为开关状态2。
(1)在开关状态1[ton期间],其等效电路图为5-2(b)。
令t=0时,开关管V导通,电源E通过V加到二极管VD和输出滤波电感L、输出滤波电容C上,故VD截止。由于输出滤波电容电压保持不变,因此加在L上的电压为 E-Uo ,这个电压差使输出滤波电感电流iL线性增加。
![]()
当 t = DTs = ton 时,iL达到最大值ILmax。
在V导通期间,iL的增量ΔiL+为


图5-2 Buck变换器电路图及波形
(2)在开关状态2[toff期间],其等效电路图为5-2(c)。
在 t>ton 时,V关断,iL通过二极管VD继续流通。此时加在L上的电压为-Uo,电感电流iL线性减小。

当t= Ts时,iL减小到最小值ILmin。
在V截止期间,iL的减小量ΔiL-为

在 t≥Ts 时,开关管V又导通,开始下一个开关周期。
在开关管V导通期间VD截止,流过开关管V的电流是电源输入的电流,也就是电感电流Li;在V截止期间,二极管VD导通时,流过二极管VD的电流是Li,这时开关管V的电流和电源的输入电流为0。为了减小电源输入电流的脉动,可在Buck变换器的输入侧加接输入LC滤波电路。稳态工作时流入电容C充电量等于放电量,通过电容的平均电流应为零,因此电感电流的平均值IL就是负载电流平均值Io。
2)电压、电流基本关系
Buck 电路处于稳定工作时在开关管V导通的ton期间,电感电流iL从ILmin线性上升至ILmax ,在随后V关断、VD导通的toff期间,iL又从ILmax线性下降到ILmin,参见图5-2(e)。V导通期间iL的增量ΔiL+等于它在V关断期间的减小量ΔiL-。
由式(5-4)和式(5-6)可以得到

定义变压比为![]() 由式(5-7)可得
由式(5-7)可得![]()
因此理想的Buck变换器在电感电流连续的情况下变压比M只与占空比D有关,与负载电流的大小无关。
稳态时,一个开关周期内滤波电容C的平均充电与放电电流相等,故变换器输出的负载电流Io就是iL的平均值IL,即

由前述假定,变换器的损耗为零,输出功率 Po =UoIo 等于输入功率 Pi =EIi ,Io和Ii分别为变换器的输出平均电流和输入平均电流。因此变压比M有可表示为
![]()
由式(5-7)、(5-8)可得,电感电流的最大值ILmax和最小值ILmin分别为
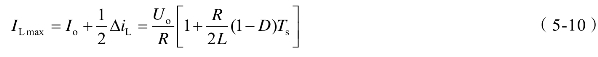

式中,![]() ,R为变换器负载电阻。
,R为变换器负载电阻。
开关管V和二极管VD截止时所承受的电压都是输入电压E。
从图5-2(a)可知,iC =iL -io ,当iL >io 时,iC为正值,电容C充电,输出电压Uo升高;当iL <io 时,iC为负值,电容C放电,输出电压Uo下降,因此电容C一直处于周期性充放电状态。若滤波电容C足够大时,则uo为平滑的直流电压。当C不够大时,则uo有一定的脉动。
电容C在一个开关周期内的充电电荷ΔQ为
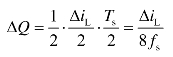
上式中的ΔLi由式(5-7)确定,因此输出电压的脉动量ΔUo为

由此可见,增加开关频率fs、加大L和C都可以减小输出电压脉动。
2.Buck变换器电感电流断续时工作特性
1)三种开关状态和变压比M
图5-2(f)给出了电感电流断续时工作电压、电流波形,此时开关管V和二极管VD有三种工作状态:
(1)[开关状态1]:V导通,VD截止ton期间,电路结构如图5-2(b)所示。在ton =DTs期间,电感电流iL从零开始线性增加到ILmax,其增量ΔiL+为

V导通,VD截止的ton =DTs 期间变换器输出电压ueo=E。
(2)[开关状态2]:V截止,VD导通toff期间,电路结构如图5-2(c)所示。令![]() ,在
,在![]() 期间,电感电流iL从ILmax线性下降到零,其下降量ΔiL-为
期间,电感电流iL从ILmax线性下降到零,其下降量ΔiL-为

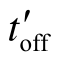 为续流二极管VD导通时间,电感电流在
为续流二极管VD导通时间,电感电流在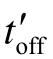 期间下降到零,
期间下降到零, 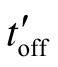 < (Ts - ton)。
< (Ts - ton)。
V截止,VD导通的 =D1Ts 期间变换器输出电压ueo=0。
=D1Ts 期间变换器输出电压ueo=0。
(3)[开关状态3]:V和VD都截止,电路结构如图5-2(d)所示。在一个周期Ts的剩余时间 (Ts - ton 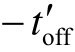 ) = Ts (1 - D - D1)期间,V、VD都截止,在此期间,电感电流iL保持为零,图5-2(a)中变换器输出电压 ueo =Uo ,负载由滤波电容供电。
) = Ts (1 - D - D1)期间,V、VD都截止,在此期间,电感电流iL保持为零,图5-2(a)中变换器输出电压 ueo =Uo ,负载由滤波电容供电。
由式(5-13)、(5-14)可得
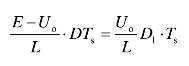
由此得到电流断续时的变压比

由于 故M>D,即电流断续时的变压比M大于导通占空比D。物理上这是由于在电感断流后,续流二极管VD又不导通,使ueo不再等于零而变为Uo,因而提高了输出直流电压平均值Uo。
故M>D,即电流断续时的变压比M大于导通占空比D。物理上这是由于在电感断流后,续流二极管VD又不导通,使ueo不再等于零而变为Uo,因而提高了输出直流电压平均值Uo。
又因为 UoIo =EIi ,故有

电感电流平均值IL就是负载电流的平均值Io,IL =Io 。
2)临界负载电流
从图5-2(e)中的电感电流波形可以看出,当负载电流Io减小时,ILmax和ILmin都减小,当负载电流Io减小到使ILmin达到零时,电感电流将在一个周期Ts中V导通的ton期间从0升至ILmax,然后在V关断的toff期间从ILmax下降到零。这时的负载电流称为临界负载电流Iob(Boundary Value)。图5-3给出了电感电流临界连续工作情况的波形。

图5-3 电感电流临界连续波形
由图5-3可知,ILmax就是导通期间电感电流的增量ΔIL+,即ILmax =ΔIL+。因此临界负载电流![]() 即
即

电感电流临界连续工作时,Uo=D·E,M=D的关系仍然成立,式(5-17)的临界负载电流可表达为

由此可得到E不变时,当D=0.5时,Iob有最大值
![]()
式(5-18)又可表示为

由此可得到Uo不变时,当D=0时,Iob有最大值
![]()
5.1.2 升压(Boost)斩波电路
像图5-1(a)那样在电源E与负载之间串接一个通-断控制的开关器件绝不可能使负载获得高于电源电压E的直流电压。为了获得高于电源电压E的直流输出电压,一个简单而有效的办法是在变换器开关管前端插入一个电感L,如图5-4(a)所示,在开关管V关断时,利用图5-4(c)中电感线圈L在其电流减小时所产生的反电动势eL(在电感电流减小时,![]() 为正值)与电源电压E串联相加送至负载,则负载就可获得高于电源电压E的直流电压Uo。
为正值)与电源电压E串联相加送至负载,则负载就可获得高于电源电压E的直流电压Uo。

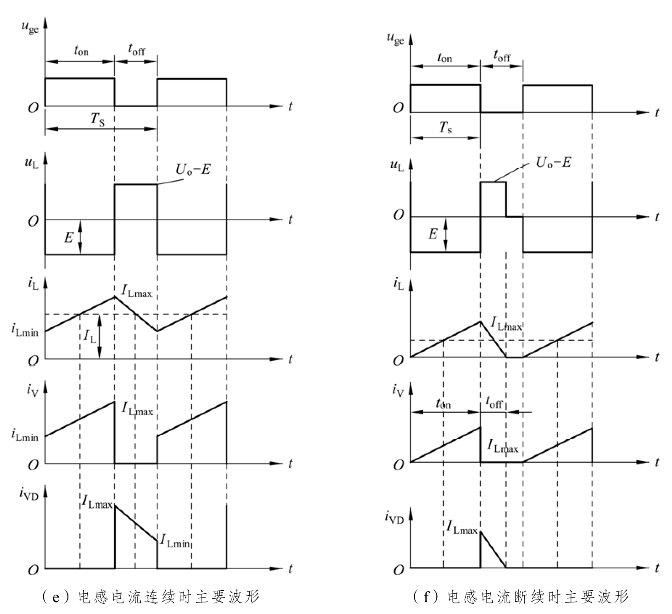
图5-4 Boost变换器电路图及波形
图5-4(a)中Boost变换器中电感L在输入侧,称之为升压电感。开关管V仍采用PWM控制方式,和Buck变换器一样,Boost变换器也有电感电流连续和断续两种工作方式,图5-4(e)和(f)给出了这两种工作方式下的波形图。图5-4(b)、(c)、(d)为Boost变换器在不同开关状态时的等效电路。当电感电流连续时,Boost变换器存在两种开关状态,如图5-4(b)和(c)所示;而当电感电流断续时,Boost变换器还有第三种开关状态,如图5-4(d)所示。
1.Boost变换器电感电流连续时工作特性
1)两种开关状态
图5-4(a)中在一个开关周期Ts的ton期间,开关管V处于导通、二极管VD处于关断状态,定义为开关状态1;在toff期间,V关断、VD导通定义为开关状态2。
(1)在开关状态1[ton期间],其等效电路图为5-4(b)。
令t=0时,开关管V导通,电源E加到升压电感L上,电感电流iL线性增加。

当 t = DTs = ton 时,iL达到最大值ILmax。
在V导通期间,iL的增量ΔiL+为(https://www.xing528.com)

在开关状态1,由于二极管VD关断,负载由电容C供电,选用足够大的C值可使uo变化很小,近似分析中可认为在一个开关周期Ts中uo恒定不变,等于其平均值Uo。
(2)在开关状态2[toff期间],其等效电路图为5-4(c)。
在 t>ton 时,V关断,这时电源电压E和电感电流iL通过二极管VD向负载和电容供电,iL减小,此时加在L上的电压为 E-Uo ,由于Uo>E,故电感电流iL线性减小。

当t= Ts时,iL减小到最小值ILmin。
在V截止期间,iL的减小量ΔiL-为
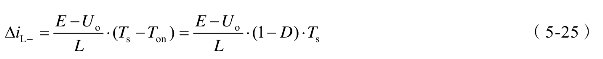
在 t≥Ts 时,开关管V又导通,开始下一个开关周期。
在开关管V导通期间VD截止,流过开关管V的电流是电源输入的电流,也就是电感电流iL;在V截止期间,二极管VD导通时,流过二极管VD的电流是iL。稳态工作时流入电容C充电量等于放电量,通过电容的平均电流应为零,因此二极管电流的平均值IVD就是负载电流平均值Io。
2)电压、电流基本关系
稳态工作时,V导通期间,电感电流iL的增量ΔiL+等于它在V关断期间的减小量ΔiL-。
从式(5-23)和式(5-25)可以得到

定义变压比为![]() 由式(5-26)可得
由式(5-26)可得![]() 。
。
在每一个开关周期中,电感L都有一个储能和能量通过二极管VD释放过程,也就是说必须有能量送到负载端。因此,如果该变换器没有接负载,则不断增加的电感储能不能释放,必然会使Uo不断升高,最后使变换器损坏。实际工作中D越接近1,输出电压越高,为防止输出电压过高,Boost变换器不宜在占空比D接近于1的情况下工作。
Boost变换器在电感电流连续的情况下变压比M只与占空比D有关,与负载电流的大小无关。
通过二极管电流的平均值IVD就是负载电流平均值Io,即IVD =Io 。电感电流的脉动量

由前述假定,变换器的损耗为零,输出功率 Po =UoIo 等于输入功率 Pi =EIi ,Io和Ii分别为变换器的输出平均电流和输入平均电流。因此变压比M有可表示为
![]()
由图5-4(e)可知,通过V和VD的电流最大值IVmax和IVDmax 与电感电流最大值ILmax相等,即

V和VD关断时所承受点电压均为输出电压Uo。
输入电流ii的脉动量Δii等于电感电流iL的脉动量ΔiL。
输出电压脉动量Δuo等于开关管V导通期间电容C向负载放电引起的电压变化量。Δuo可近似地由下式确定:
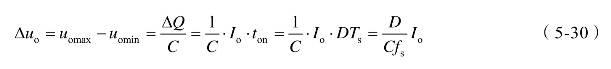
因此

其中
![]()
由此可见,增加开关频率fs、加大R和C都可以减小输出电压脉动。
2.Boost变换器电感电流断续时工作特性
1)三种开关状态和变压比M
图5-4(f)给出了电感电流断续时工作电压、电流波形,此时开关管V和二极管VD有三种工作状态:
(1)[开关状态1]:V导通,VD截止ton期间,电路结构如图5-4(b)所示。在ton =DTs期间,电感电流iL从零开始线性增加到ILmax,其增量ΔiL+为

上式中![]() 为开关频率。
为开关频率。
(2)[开关状态2]:V截止,VD导通toff期间,电路结构如图5-4(c)所示。令![]() 在
在![]() 期间,电感电流iL从ILmax线性下降到零,其下降量ΔiL-为
期间,电感电流iL从ILmax线性下降到零,其下降量ΔiL-为
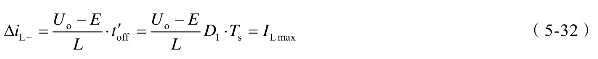
 为二极管VD导通时间,电感电流在
为二极管VD导通时间,电感电流在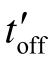 期间下降到零,
期间下降到零, < (Ts - ton)。
< (Ts - ton)。
(3)[开关状态3]:V和VD都截止,电路结构如图5-4(d)所示。在一个周期Ts的剩余时间 ![]() 期间,V、VD都截止,在此期间,电感电流iL保持为零,负载由电容供电。
期间,V、VD都截止,在此期间,电感电流iL保持为零,负载由电容供电。
由式(5-31)、(5-32)可得

由此得到电流断续是的变压比
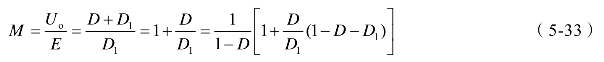
由上式可知,![]() 即电流断续时的变压比大于电流连续时的变压比。
即电流断续时的变压比大于电流连续时的变压比。
又因为 UoIo =EIi ,故有

由图5-4(a)可知,电感电流平均值IL就是电源电流的平均值Ii,IL =Ii 。
2)临界负载电流
从图5-4(e)中的电感电流波形可以看出,当负载电流Io减小时,ILmax和ILmin都减小,当负载电流Io减小到使ILmin达到零时,电感电流将在一个周期Ts中V导通的ton期间从0升至ILmax,然后在V关断的toff期间从ILmax下降到零。这时的负载电流称为临界负载电流Iob(Boundary Value)。图5-5给出了电感电流临界连续工作情况的波形。

图5-5 电感电流临界连续波形
由图5-5可知,在toff期间,V关断,VD导通,电感电流iL下降,这时iL =iVD ,当电路处于稳态时,在一个周期Ts中,电容电流的平均值为零,由图5-4(a)可以得到,二极管电流平均值IVD就等于负载电流平均值Io,因此可以得到临界负载电流Iob为
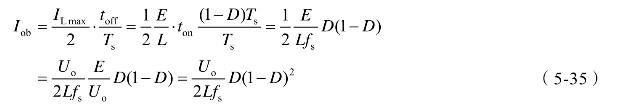
由此可得到E不变时,当D=0.5时,Iob有最大值
![]()
Uo 不变时,当D=1/3时,Iob有最大值
![]()
当负载电流 Io >Iob 时,电感电流连续,变压比 M = 1/(1 -D),Uo = E /(1- D);
当负载电流 Io =Iob 时,电感电流临界连续,变压比仍然 M = 1/(1 -D),Uo = E /(1- D);
当负载电流 Io <Iob 时,电感电流断续续,变压比 M > 1/(1 - D)。
5.1.3 降升压(Buck-Boost)斩波电路
前述Buck电路只能降压,Boost电路只能升压。有没有一种电路既可以实现降压变换又可实现升压变换?即输出电压直流平均值即可以Uo≥E,也可以Uo≤E。图5-6给出了Buck-Boost变换器电路,为了分析方便起见,假设电路中的电感L和电容C都很大,因此电感电流iL和负载电压uo视为恒定不变。
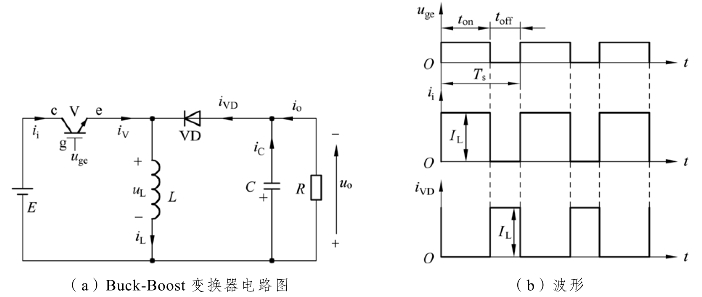
图5-6 Buck-Boost变换器电路及波形
V导通时,电源E经V向L供电使其贮能,此时电流为ii,同时C维持输出电压恒定并向负载R供电。工作电路存在电流回路E → V →L → E 和C → R→ C 。
V关断时,L释放电能,电流为iVD;C处于充电状态;负载电压极性为上负下正,与电源电压极性相反,该电路也称作反极性斩波电路。此阶段,电路中的电流回路为L → C//R → VD → L 。
稳态时,一个周期T内电感L能量平衡,即储能量等于放电量。且大电感电流恒定,所以电感两端电压uL对时间的积分为零,即

V导通时,uL=E;而当V处于断态期间,uL =-u0,则
![]()
所以输出电压为

改变导通比D,输出电压既可以比电源电压高,也可以比电源电压低。当0<D<1/2时为降压,当1/2<D<1时为升压,因此将该电路称作升降压斩波电路。设电源电流ii和负载电流io的平均值分别为Ii和Io,当电流脉动足够小时,有

进一步,

如果V、VD为没有损耗的理想开关时,则输出功率和输入功率相等,即
![]()
5.1.4 升降压(Boost-Buck)斩波电路或Cúk(丘克)电路
Cúk变换器是把Boost与Buck变换器先后串联起来,进行如下的演变,从而得出很有特色的一个直流-直流变换电路。
在升压变换器后串一个降压变换器的电路,如图5-7(a)所示。假定在图5-7(a)中,开关V1和V2是同步的,并有相同的占空比D,则S1、VD1、S2、VD2的功能可以用等效的双刀双掷开关S来代替,得到图5-7(b)所示电路。如果允许输出电压是反极性时,则双刀双掷开关及并联电容器C1可以用一个单刀双掷的开关S及一个串联电容器C1代替,这时图5-7(b)就可以简化为图5-7(c)。再进一步用一个开关管V和一个二极管VD代替图5-7(c)中的单刀双掷开关S,则得到一个直流-直流升/降压变换电路,如图5-7(d)所示,这就是C úk变换器。


图5-7 Cúk斩波电路及其等效电路
下面对其工作原理进行分析。电路稳定工作后,当V导通时,电路中存在电流回路E → L1 →V →E 、C1 → V → R/ /C2 → L2。在此阶段,电感L1储能,电容C1释放电能,电感 L2储能。当V关断后,电路中存在电流回路 E →L1 → C1 → VD →E 和L2 → VD → R//C2 →L2。在此阶段,电感L1和电源E共同为电容C1充电,电感 L2为负载R供电。经上述分析,实际电路可简化为图5-7(c)所示的等效电路,工作过程相当于单刀双掷开关S在A、B两点间反复切换。
C1的电流在一周期内的积分应为零,即

在V导通期间ton和关断期间toff,流经电容C1的电流分别为-iL2和iL1。假定电感L1和L2足够大,那么iL1和iL2分别等于其平均值IL1和IL2,因为 IL1 =Ii 和 IL2 =Io ,则有
![]()
可求出

接下来分析稳态时输出电压Uo与输入电压E之间关系。设电容C1很大,电容电压恒定为UC1,当开关S打向B点时,uB=0,uA =-UC1;当开关S打向A点时,uB =UC1,uA=0。因此,B点平均电压为![]() 由于电感L1的平均电压为零,则有
由于电感L1的平均电压为零,则有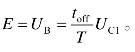 同理,A点平均电压为
同理,A点平均电压为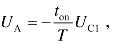 电感 L2的平均电压也为零,可求出
电感 L2的平均电压也为零,可求出![]() 最后可得
最后可得

由于电感 L1和 L2分别对电流ii和io起到了平波作用,因此与升降压斩波电路相比,Cúk斩波电路具有输入与输出电流都为连续、脉动小的突出优点。
5.1.5 Sepic斩波电路和Zeta斩波电路
图5-8中的(a)、(b)两图分别是Sepic斩波电路、Zeta斩波电路的原理图。

图5-8 Sepic斩波电路和Zeta斩波电路
Sepic斩波电路原理:
工作原理为:V导通时, E → L1 → V → E 回路和 C1 →V→ L2 →C1回路同时导电,L1和L2贮能。V关断时, E → L1 → C1 → VD →负载→ E 及 L2 → VD →负载→ L2同时导电,此阶段E和L1既向负载供电,同时也向C1充电(C1贮存的能量在V处于通态时向L2转移)。
输入输出电压关系为

Zeta斩波电路原理:
工作原理为:V导通时,电源E经开关V向电感L1贮能。V关断时,L1 →VD →C1 →L1构成振荡回路,L1的能量转移至C1,能量全部转移至C1上之后,VD关断,C1经L2向负载供电。
输入输出关系为

两种电路具有相同的输入输出关系,Sepic电路中,电源电流连续但负载电流断续,有利于输入滤波,反之,Zeta电路的电源电流断续而负载电流连续;两种电路输出电压为正极性的。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




