多电平逆变器的拓扑结构及电容钳位式多电平逆变电路简介

电平数，在逆变输出的电压波形中，一般都不是标准的正弦波，而是阶梯波的形式。那么从电压最高值到最低值之间形成的阶梯数就称为电平数。

传统逆变器电路结构简单，输出电平数较少，所以输出含有大量谐波，这无疑给逆变电源输出滤波电路的设计带来了很大的麻烦，因此诸多学者开始寻求解决问题的办法，多电平逆变电路便是在这种情况下应运而生。1980年，日本学者A.Nabae首次提出中点钳位型三电平逆变电路，这是多电平逆变电路第一次为世人所知，它的出现对逆变电路来说意义重大。

所谓多电平逆变电路，其实际上是在传统逆变电路基础上的改进，它是一种通过改变逆变电路结构以达到提高输出电压和功率的新型逆变电路。与一般逆变电路相比，其输出电平数更多，输出谐波含量更少，具有更好的输出特性，此外，随着电路结构的改变，单个开关器件所承受的电压也随之减少，大大提高电路的可靠性。

经过多年的发展研究，多电平逆变技术越发成熟，至今，主要可分为以下三种：飞跨电容型多电平逆变电路、中点钳位型多电平逆变电路、H桥级联式多电平逆变电路，其单相电路拓扑结构如图4-19所示。

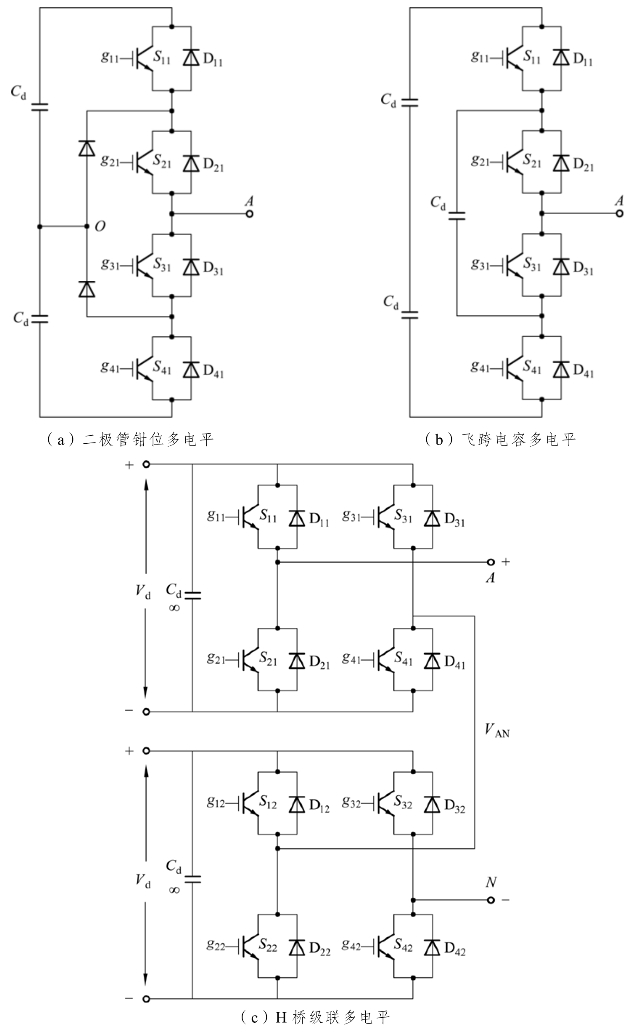
图4-19 多电平逆变器的拓扑结构（单相）

飞跨电容型多电平逆变电路又称为电容钳位式多电平逆变电路，顾名思义，该电路主要利用电容对开关管电压进行钳位，因此该电路并不存在功率开关器件的电压不平衡问题和二极管不能快速反向恢复的问题。该电路虽然较一般电路有明显优势，但是也存在诸多的问题，如：① 随着逆变电路输出电平数的增加，电路中所需用作钳位的电容也越多，较多数量的钳位电容大大增加了电路的成本，同时，多个钳位电容的电压不平衡问题使得电路的控制变得更加的复杂；② 系统启动时，各个钳位电容需要进行充电，降低了系统的效率；③ 因为电路中有较多数量的电容，所以电路在高频工作时损耗较大。

中点钳位型多电平逆变电路也叫作二极管钳位式多电平逆变电路，不同于电容钳位式电路利用电容钳位，其对功率开关器件的钳位采用的是二极管，而且，电容在其中的作用不是电容钳位式电路中的钳位作用而是均压作用。这种电路通过串联电容对电源进行均压，从而得到一组较之前更低的电压值，进而得到更多的输出电平。对于二极管钳位式逆变电路来说，如果想要得到数目为N的输出电平，那么就需要在逆变电路的直流侧串联数目为N－1的电容，这些电容将电路直流侧电源电压进行均分，而后利用二极管将单个开关管的电压值固定为U/N（U为逆变电路直流侧电源电压值），这样便大大增多了电路的输出电平数，使电路具有更好的输出特性。

同电容钳位式多电平逆变电路一样，二极管钳位式多电平逆变电路虽然成功地增加了电路输出的电平数，大大降低了电路输出的谐波含量，改善了电路的输出特性，但是其自身也仍然存在着一定的缺陷，其缺点如下：① 因为中点钳位型电路需要大量的二极管对开关器件的电压进行钳位，所以电路中的器件数目较多，这不仅使得电路结构更加复杂化，而且大大增加了系统的成本；② 电路使用电容对直流侧电源分压要求做到平均分配，故电容电压的不均衡便又是其一大问题，且随着所需输出电平数的增多，电容数目也相应地增加，电路的控制也越发的复杂。

中点钳位型和电容钳位式多电平逆变电路虽然在传统逆变电路的基础上得到了改进，也实现了输出的多电平化，但是两者均存在电容分压不均的问题，控制也较为复杂，而新的电路拓扑结构的出现恰好解决了这一难题。H桥电路作为新型的多电平电路结构，不同于前两种电路结构的电容分压，H桥电路是以传统的两电平逆变电路为基本单元进行的电路的串联，其通过串联多个小功率单元达到大功率输出的目的，其中各个基本单元电源独立，因此并不存在电容分压不平衡的问题。

按照基本单元电路结构的相同与否，其大致可分为两类：① 当构成H桥电路的基本单元电路结构相同时，这样的H桥电路称之为对称H桥电路；② 反之，当组成H桥电路的基本单元的电路结构不同时，它们组成的电路称之为非对称H桥电路。

H桥逆变电路虽然解决了电压不平衡问题，但是有利便有弊，H桥逆变电路在解决问题的同时难免会产生新的问题，如：① 因为H桥采用多个电路单元串联，而且每个电路单元电源独立，所以H桥电路需要多个独立的直流电源，这为系统的设计增加了难度，也增加了系统的体积；② H桥电路串联单元分别独立，各自拥有独立的直流电源，因此整个电路很难实现四象限运行。

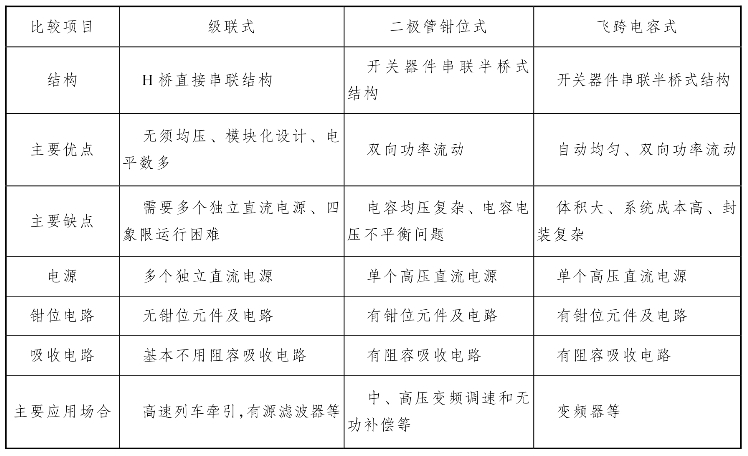
三种多电平逆变器优缺点比较见表4-5。

表4-5 三种多电平逆变器的拓扑结构比较

下面以级联式多电平为例讲述多电平逆变器的工作原理及调制策略。串联H桥逆变器采用由多个直流电源分别供电的H桥单元，各单元的输出串联连接以输出高交流电压。一种典型的5电平串联H桥逆变器结构如图4-20所示，其中每相有两个H桥单元，分别由电压为dV的两个独立直流电源供电。

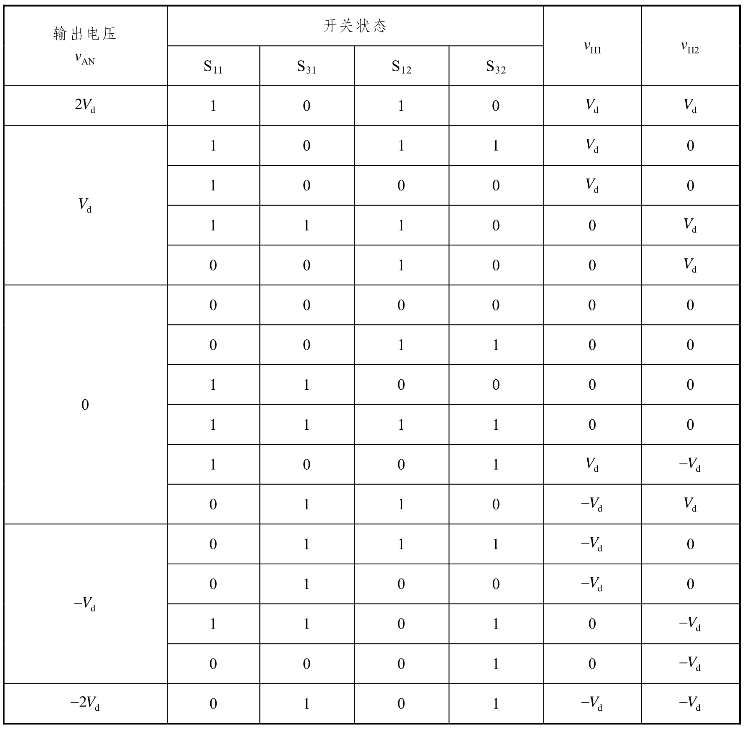
图4-20中所示的逆变器每相可输出含有5个不同电平的相电压。当S11，S21，S12和S22导通时，H桥单元H1和H2的输出都为Vd，即vH1 =vH2 =Vd 。则逆变器输出的相电压，例如端点A相对于逆变器中性点N的电压，为vAN = vH1 + vH2 = 2Vd 。与此类似，当S31，S41，S32和S42导通时， vAN =-2Vd 。其他三个可以输出的电压电平分别为Vd，0和 -Vd，它们分别对应不同的开关状态组合，详见表4-6。需要指出的是，逆变器输出的相电压vAN并不一定要和负载相电压vAO相等，其中vAO为负载侧端点A相对于负载的中性点O的电压。(www.xing528.com)

从表4-6中可以看出，某些电压电平可由超过一种的开关状态实现。例如，对于电压V，d它可以由四种不同的开关状态实现。这种冗余性的开关状态在多电平逆变器中非常普遍，使开关状态的设计变得很灵活。串联H桥逆变器输出电压的电平数m可由下式计算

其中，H为每相中H桥单元的数目。由上式看出，这种逆变器的电平数目总是奇数。在其他类型的多电平逆变器中，例如二极管钳位式中的输出电平数目可以是奇数，也可以是偶数。

图4-21给出了移相载波调制法的规则。其中包含4个三角载波，任意相邻的载波有90°的相移。为简单起见，图中只给出了A相的调制波vmA。载波vcr1和vcr2分别用来产生H桥单元H1和H2左桥臂上部二个开关器件S11和S12的栅极信号。其余两个载波vcr1-和vcr2-与载波vcr1和vcr2分别有180°的相移，分别用来产生H桥单元右桥臂上部三个开关器件S31和S32的栅极信号。所有H桥单元下部开关器件的栅极信号，在图中没有给出，它们可由对应上部器件的栅极信号进行互补得到。

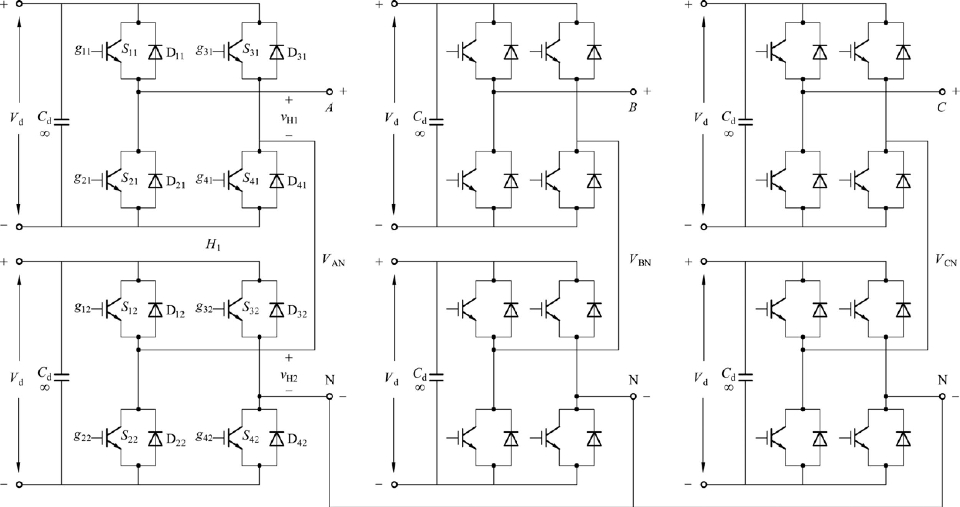
图4-20 级联五电平电路拓扑结构

表4-6 五电平串联H桥逆变器的输出电压与其对应的开关状态

上面讨论的PWM控制法本质上为单极性调制法。例如在图4-21中，H桥单元H1上部开关器件S11和S31的栅极信号是由载波信号vcr1和vcr1-与调制波vmA进行比较得到。H1的输出电压vH1，正半个基波周期时，在0和Vd之间切换；负半个基波周期时，在 -Vd和0之间切换。在这个例子中，频率调制比为 mf =fcr/fm = 9，幅值调制比为 其中，fcr，fm 分别为载波频率和调制波频率；和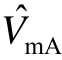分别为vcr和vmA的峰值。

逆变器的输出相电压为

其中，vH1和vH2分别为H桥单元H1和H2的输出电压。可明显看出，逆变器的输出相电压由2Vd ，Vd，0， -Vd和-2Vd等5个电压电平构成。

图4-21 单相2H桥逆变器的载波移相调制法波形图（ma=0.8，mf=9）

为了验证上述的分析，采用MATLAB/Simulink对图4-20所示的拓扑结构电路进行仿真，其中，直流母线电压为Vd=510 V，幅度调制比为0.8，基波频率为50 Hz，开关频率为450 Hz，等效开关频率为1.8 kHz。图4-22为其仿真波形，由图4-22（a）可知，单个H桥输出的电压波形为单极性波形，这符合上述分析的单个H桥采用单极倍频调制方式；由图4-22（b）可知，2H桥电路的输出为5电平，最低次谐波在36次附近，达到4倍频的效果。

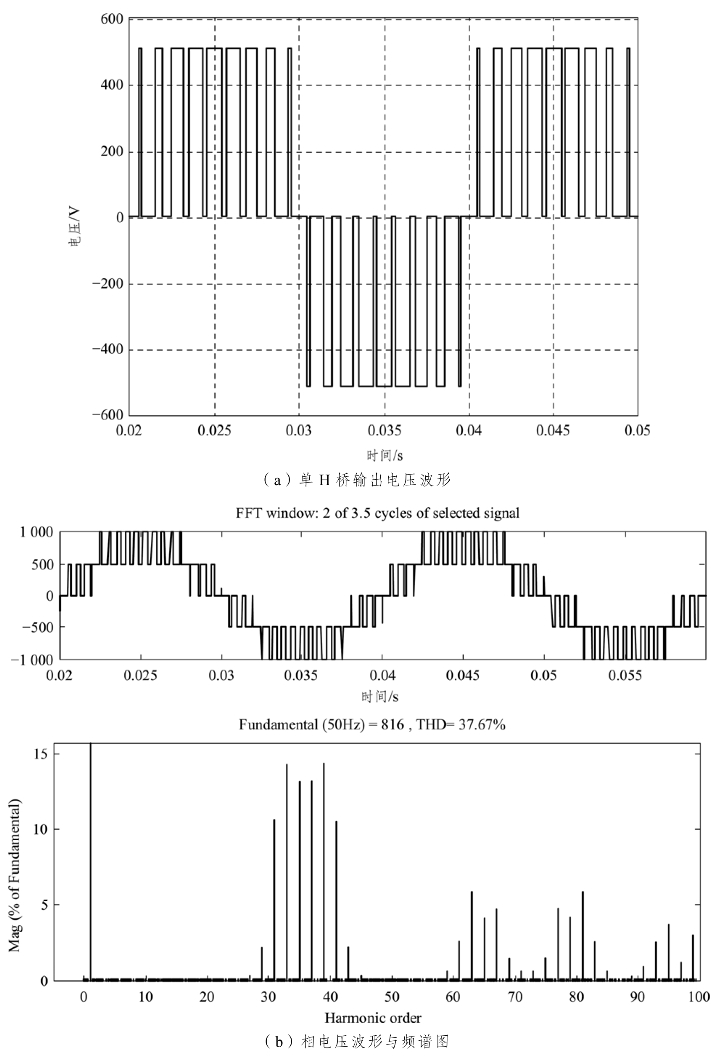
图4-22 仿真波形