三相电压源型逆变器及调制技术

电压源型逆变器的主要功能，是将恒定的直流电压转换为幅值和频率可变的三相交流电压。图4-12给出了两电平电压源型逆变器（以下简称为两电平逆变器）的简化电路框图。该逆变器主要由六组功率开关器件S1～S6组成，每个开关反并联了一个续流二极管。根据逆变器工作的直流电压不同，每组功率器件可由两个或多个电力电子器件串联组成。

图4-12 三相电压型桥式逆变器

例4-1 在图4-12中，设直流电源电压 Vd = 200 V，则在开关器件断态时，开关器件所承受的电压是多少？

解：考虑同一桥臂上开关器件S1和S4。在电压型逆变电路中，同一桥臂上的开关器件是互补导通的。当开关器件S1导通时，开关器件S4是关断的。假定开关器件是理想的，其导通管压降等于零，则开关器件S4在断态时承受的电压等于直流电压电压Vd，即200 V。其他器件的分析类似。

4.3.1 调制方法

三相电压型桥式逆变电路的基本工作方式为180°导电方式，即每个桥臂的导电角度为180°，同一相上下两个桥臂交替导电，各相开始导电的角度依次相差120°，这样，在任一瞬间，将有三个桥臂同时导通。可能是上面二个臂下面一个臂，也可能是上面一个臂下面二个臂同时导通。因此每次换流都是在同一相上下两个桥臂之间进行，因此也称为纵向换流。

下面来分析三相电压型桥式逆变电路的工作波形。对于A相输出来说，当上桥臂开关器件S1导通时，vAN =Vd ，当下桥臂开关器件S4导通时，vAN=0。因此，vAN的波形是幅值为vAN =Vd 的矩形波。B、C两相的情况和A相类似，vBN、vCN的波形形状和vAN相同，只是相位依次差120°。vAN、vBN、vCN的波形如图4-13（a）所示。

逆变器的线电压vAB可由式vAB = vAN - vBN 计算得到，其为120°矩形波。其基波分量vAB1也已在图4-13（a）中给出。

同理vBC = vBN - vCN ，vCA= vCN- vAN ，其也为120°矩形波。

在有些场合只需要求出线电压即可，比如负载为△联结或负载虽然为Y联结但负载中心点没有引出，对于△联结，其线电压等于相电压。但有些场合还需求出相电压vAO、vBO、vCO的波形。

列写方程

由①－③得

设负载为对称负载，则有vAO +vBO +vCO=0，故可得

同理可得

vAO 的波形如图4-13（a）所示，vBO、vCO的波形和vAO相同，仅相位依次相差120°。

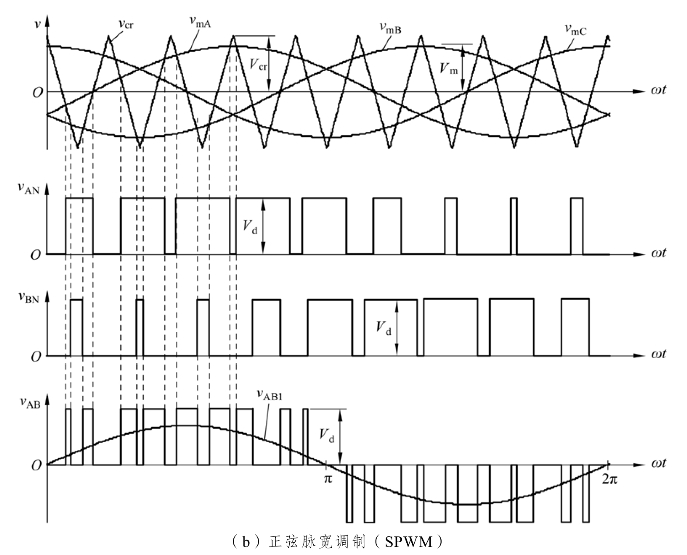
图4-13 两电平三相逆变器调制方法

下面对三相桥式逆变电路的输出电压进行定量分析。把输出线电压vAB展开成傅立叶级数得

输出线电压的有效值VAB为

基波幅值VAB1m和有效值VAB1分别为

对负载相电压vAB展开成傅立叶级数得

负载相电压的有效值VAO为

基波幅值VAO1m和有效值VAO1分别为

图4-13（a）所述的三相电压型逆变器每个开关器件在一个开关周期中仅通、断状态转换一次，输出线电压每半周中仅一个脉冲电压（120°方波），负载为Y联结时，负载相电压为阶梯波，逆变器输出电压中的基波仅取决于直流电压dV的大小而不能调节控制，最低为5次谐波，且谐波含量大（占基波含量的20%）。这种情况相当于单相电压型逆变器单脉波脉宽θ=120°导电方式。

对于三相逆变器同样可以采用SPWM控制方式。在输出电压的每一个周期中，各开关器件通、断转换多次，实现既可调节控制输出电压的大小，又可消除低次谐波改善输出波形。

图4-13（b）给出了两电平逆变器正弦脉宽调制方法的原理。其中，vmA、vmB和vmC为三相正弦调制波，vcr为三角载波。逆变器输出电压的基波分量可由幅值调制比 ma控制。

开关器件S1～S6的控制取决于调制波与载波的比较结果。例如，当vmA ≥vcr 时，逆变器A相上桥臂开关器件S1导通，而对应的下桥臂S4工作在与S1互补的开关方式，故此时关断。由此产生的逆变器终端电压vAN（即A相输出节点与负直流母线N之间的电压）等于直流电压 Vd。当 vmA ＜vcr 时，S4导通而S1关断，因此vAN=0，如图4-13（b）所示。

逆变器的线电压vAB可由式vAB = vAN - vBN 计算得到，其基波分量vAB1也已在图4-13（b）中给出。电压vAB1的幅值和频率可分别由 ma和fm控制。

两电平逆变器的开关频率可由式 fsw = fcr = fm × mf 计算得到。例如，图4-13（b）中vAN的波形在每个基波周期内有9个脉冲，而每个脉冲由S1开通和关断一次所产生。如果基频为50 Hz，则S1的开关频率为fsw = 50Hz× 9 = 450Hz ，这与载波频率fcr也是相等的。值得注意的是，在多电平逆变器中，器件的开关频率并不总是等于载波频率。这个问题将在后续章节讨论。

如果载波与调制波的频率是同步的，即 mf为固定的整数，则称这种调制方法为同步PWM。反之则为异步PWM，其载波频率fcr通常固定，不受fm变化的影响。异步PWM的特点在于开关频率固定，易于用模拟电路实现。不过，这种方式可能产生非特征性谐波，即谐波频率不是基频的整数倍。同步PWM方法更适用于数字处理器实现。

例4-2 三相桥式电压型逆变电路，图4-13（a）所示的180°导电模式，直流电源电压Vd = 200V 。试求输出线电压vAB的有效值VAB，输出线电压基波vAB1的幅值VAB1m及有效值VAB1。

解：

例4-3 三相桥式电压型逆变电路，图4-13（b）所示的正弦脉宽调制方式，调制度为ma = 0.8，直流电源电压Vd = 200V 。试求输出线电压基波vAB1的有效值VAB1及幅值VAB1m。

解：

图4-14给出了两电平逆变器的一些仿真波形。其中，vAB为逆变器的线电压，vAO为负载相电压，iA为负载电流。逆变器工作于ma=0.8、mf=15、 fm = 50Hz 、 fsw = 750Hz 以及额定三相感性负载的条件下，每一相负载功率因数均为0.9。从图中可以看出：

● vAB的谐波中所有低于（mf-2）次的谐波均被消除；

● 谐波的中心频率为 mf及其整数倍，如2mf和3mf等。

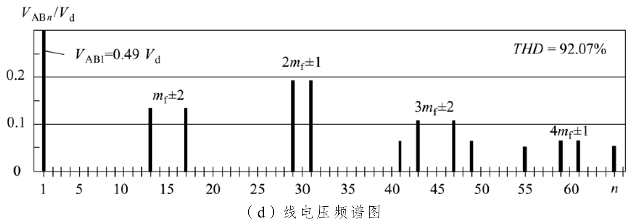
图4-14 两电平逆变器的仿真波形（ma=0.8，mf=15， fm = 50Hz ， fsw = 750Hz ）

在mf≥9，且 mf为3的整数倍的情况下，上述结论均成立。

负载电流iA的波形近似正弦，其总谐波畸变率（THD）为7.73%。其谐波畸变比较低，原因在于调制方法对低次谐波的抑制作用以及负载电感的滤波作用。

图4-15给出了逆变器线电压vAB的谐波分量随 ma变化的曲线。其中，vAB以直流电压Vd为基值进行了标幺化处理，VABn为第n次谐波电压的有效值。可以看出，基频分量VAB1随 ma呈线性变化，当 ma= 1时，其最大值为

图中也同时给出了vAB的THD变化曲线。

图4-15 电压vAB的谐波成分

4.3.2 SVPWM调制

上节讲述了两电平SPWM的原理以及其实现方法。本节将讲述两电平SVPWM的原理。由上节内容不难发现SPWM控制方式是为了得到近似正弦的电压波形。但是在电机的控制中，最终目标是使得异步电机内部产生圆形旋转磁场，从而使得电磁转矩恒定而没有脉动。如果把产生圆形旋转磁场作为控制异步电机的目标，那么逆变器产生的电磁转矩的脉动就会大大减少。称这种控制方式为“磁链跟踪控制”。由于在控制的过程中，磁链是由电压空间矢量来控制的，因此，也可将这种控制方法称为“电压空间矢量脉宽调制”。即SVPWM。空间矢量调制（SVPWM）是一种性能非常好的实时调制技术，目前广泛应用于异步电机控制、数字控制的电压源型逆变器中。

开关状态：

图4-12所示两电平逆变器的开关工作状态可表述为开关状态，如表4-1所示。其中，开关状态“1”表示逆变器一个桥臂的上管导通，从而端电压（vAN,vBN 或vCN）为正（+Vd）；开关状态“0”表示桥臂的下管导通，使得逆变器输出端电压为零。

表4-1 开关状态定义

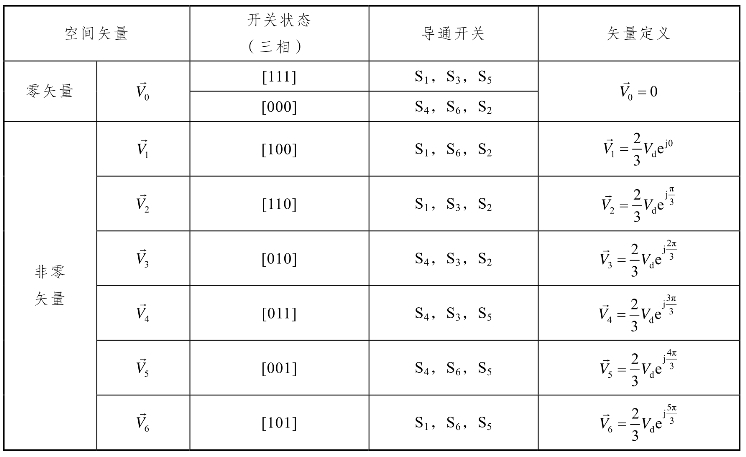
两电平逆变器有8种可能的开关状态组合，在表4-2中全部给出。例如，开关状态[100]分别对应逆变器A、B和C三相桥臂开关S1、S6和S2导通。在这8种开关状态中，[111]和[000]为零状态，其他均为非零状态。

表4-2 空间矢量、开关状态与导通开关

空间矢量：

零与非零开关状态分别对应零矢量和非零矢量。图4-16给出了典型的两电平逆变器空间矢量图。其中，六个非零矢量组成一个正六边形，并将其分为1～6六个相等的扇区。零矢量位于六边形的中心。

图4-16 两电平逆变器的空间矢量图(www.xing528.com)

可参考图4-12来推导空间矢量与开关状态之间的关系。假设逆变器工作于三相平衡状态，则有

式中，vAO、vBO和vCO为负载瞬时相电压。

从数学运算角度考虑，三相电压中的一相为非独立变量，因为任意给定两相电压，即可计算出第三相电压。因此，可将三相变量等效转换为两相变量：

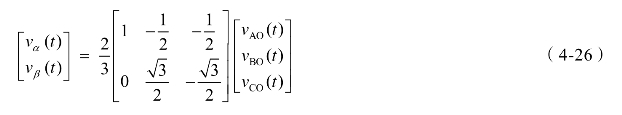
上式中，系数2/3在某种程度上是任意选定的，常用的系数值为2/3或者采用2/3的优点在于，经过等效变换后，两相系统的电压幅值与原三相系统的电压幅值相等。空间矢量通常是根据α-β坐标系中的两相电压来定义的，如下式所示

将式（4-26）代入到式（4-27）中，可以得到

式中， e jx = cos x + jsin x，且x=0、2π/3或4π/3。

非零开关状态[100]所产生的负载相电压为

将式（4-29）代入到（4-28）中，可得到对应的空间矢量

采用相同的方法，我们可推导得到所有的六个非零矢量

零矢量有两种开关状态[111]和[000]，其中的一个看起来似乎是多余的。在后续章节中会讨论冗余开关状态的作用，如用于实现逆变器开关频率的最小化或其他功能。表4-2给出了空间矢量与对应的开关状态之间的关系。

应该注意的是，零矢量和非零矢量在矢量空间上并不运动变化，因此亦可称为静态矢量。与此相反，图4-16中的给定矢量在空间中以ω的角速度旋转，即

式中，f1为逆变器输出电压的基频。

矢量相对于 α-β坐标系α轴的偏移角度θ(t)为

当给定幅值和角度位置，矢量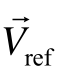可由相邻的三个静态矢量合成得到。基于这种方法，可以计算得到逆变器的开关状态，并产生各功率开关器件的门极驱动信号。当逐一经过每个扇区时，不同的开关器件组，将会不断地导通或关断。每当在矢量空间上旋转一圈，逆变器的输出电压也随之变化一个时间周期。逆变器的输出频率取决于矢量的旋转速度，而输出电压则可通过改变的幅值来调节。

作用时间计算：

上一节提到，矢量可由三个静态矢量合成。静态矢量的作用时间，本质上就是选中开关器件在采样周期Ts内的作用时间（通态或断态时间）。作用时间的计算基于“伏秒平衡”原理，也就是说，给定矢量与采样周期Ts的乘积，等于各空间矢量电压与其作用时间乘积的累加和。

假设采样周期Ts足够小，可认为给定矢量在周期Ts内保持不变。在这种情况下，可近似认为两个相邻非零矢量与一个零矢量的叠加。例如，当位于第1扇区时，它可由矢量和合成，如图4-17所示。根据伏秒平衡原理，有下式成立

式中，Ta、Tb和T0分别为矢量和的作用时间。式（4-34）所示的空间矢量可表示为

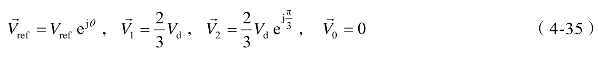
将式（4-35）代入到（4-34）中，并将结果分为 -αβ坐标系的实轴（α轴）和虚轴（β轴）分量两部分，可得到

将式（4-36）与条件 Ts = Ta + Tb + T0联立求解，得到

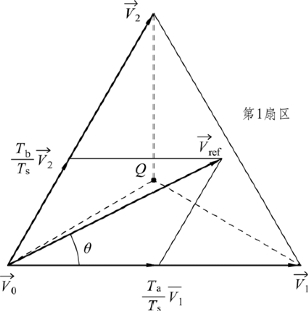
图4-17 和 合成

为了更形象地描述矢量的位置与作用时间之间的关系，我们可通过一些特殊情况进行检验和说明。如果刚好位于和的中间（即θ=π/6），的作用时间Ta将等于的时间bT。当更靠近时，Tb将大于 Ta。如果与重合，则 Ta为0。另外，如果矢量的端部刚好位于三角形中心Q，则有Ta =Tb =T0。表4-3总结了矢量的位置与其作用时间之间的关系。

另外需要注意的是，式（4-37）是以位于第1扇区为前提推导得到的。当位于其它扇区时，该式在采用变量置换后依然成立。也就是说，将实际角度θ减去π/3的整数倍，使修正后的角度θ′位于0～π/3，如下式所示：

式中，k为相应扇区的编号（1～6）。例如，当位于第2扇区时，基于式（4-37）和（4-38）计算得到的作用时间Ta、Tb和T0，分别对应矢量 和 。

表4-3 位置与作用时间

调制比：

式（4-37）也可以表示为调制比 am的形式，如下式所示：

其中，

给定矢量的最大幅值 Vref,max 取决于图4-16所示六边形的最大内切圆的半径。由于该六边形由六个长度为2Vd/3的非零矢量组成，因此可求出 Vref,max 的值为

将式（4-41）代入（4-40）中，可知调制比的最大值为

由此可知，SVPWM方案的调制比为

而其线电压基波的最大有效值则可由下式计算得到：

式中，为逆变器相电压基波的最大有效值。

对于采用SPWM控制的逆变器，线电压的基波最大值为

由此可得

式（4-45）表明，对于相同的直流母线电压，基于SVPWM的逆变器最大线电压要比基于SPWM的高15.5%。

开关顺序：

前面介绍了空间矢量选取及其作用时间的计算方法，下一步要解决的问题就是如何安排开关顺序。一般说来，对于给定的矢量其开关顺序的选取方案并不是唯一的，但是为了尽量减小器件的开关频率，需要满足下列两个条件：

a.从一种开关状态切换到另一种开关状态的过程中，仅涉及逆变器某一桥臂的两个开关器件：一个导通，另一个关断；

b.矢量在矢量图中从一个扇区转移到另一个扇区时，没有或者只有最少数量的开关器件动作。

图4-18给出了一种典型的七段法开关顺序以及矢量在第1扇区时逆变器输出电压的波形。其中，由和 三个矢量合成。在所选扇区内，将采样周期sT分为七段，可以看出：

图4-18 位于第1扇区时的七段法开关顺序

● 七段作用时间的累加和等于采样周期，即Ts = Ta + Tb + T0；

● 设计方案的必要条件（a）得以满足。例如，从状态[000]切换到[100]时，S1导通而S4关断，这样仅涉及两个开关器件；

● 冗余开关状态 用于降低每个采样周期的开关动作次数。在采样周期中间的T0/2区段内，选择开关状态[111]，而在两边的T0/4区段内，均采用开关状态[000]；

● 逆变器的每个开关器件在一个采样周期内均导通和关断一次。因此，器件的开关频率fsw 等于采样频率fsp，即 fsw = fsp = 1/Ts 。

表4-4给出了在所有六个扇区时的七段法开关顺序。需要注意的是，所有的开关顺序都是以开关状态[000]来起始和结束的，表明从一个扇区切换到下一个扇区时，并不需要任何额外的切换过程。这样，满足了前面所述的开关顺序设计要求（b）。

表4-4 七段法开关顺序