电容滤波不可控整流电路的优化方案

3.4.1 电容滤波的单相桥式不可控整流电路

电容滤波的不可控整流电路在交-直-交变频器、不间断电源、开关电源等应用场合中，大量应用。最常用的是单相桥式和三相桥式两种接法。由于电路中的电力电子器件采用整流二极管，故也称这类电路为二极管整流电路。

1.基本工作过程

电容滤波的单相桥式不可控整流电路及其工作波形如图3-30所示，在u2正半周过零点至ωt= 0期间，因 u2 ＜ud ，故二极管均不导通，电容C向R放电，提供负载所需电流。

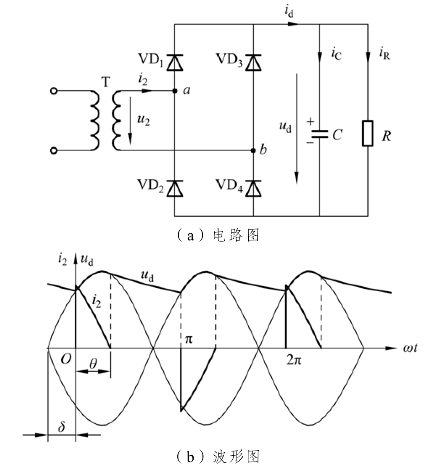
图3-30 电容滤波的单相桥式不可控整流电路及其工作波形

至ωt=0之后，u2将要超过ud，使得VD1和VD4开通，ud =u2，交流电源向电容充电，同时向负载R供电。

电容被充电到t=θ时，ud =u2，VD1和VD4关断。电容开始以时间常数RC按指数函数放电。

当t=π，即放电经过π-θ角时，ud降至开始充电时的初值，另一对二极管VD2和VD3导通，此后u2又向C充电，与u2正半周的情况一样。

2.δ 和θ 的确定

δ 指VD1和VD4导通的时刻与u2过零点相距的角度，θ 指VD1和VD4的导通角。

在VD1和VD4导通期间

式中，ud(0)为VD1、VD4开始导通时刻直流侧电压值。

将u2代入并求解得

而负载电流为

于是

设VD1和VD4的导通角为q，则当ωt=q时，VD1和VD4关断。将id(q)=0代入式（3-48），得

二极管导通后u2开始向C充电时的ud与二极管关断后C放电结束时的ud相等，故有下式成立：

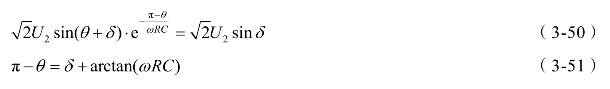
由式（3-49）和（3-50）得

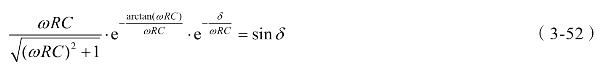
可由式（3-52）求出δ，进而由式（3-51）求出θ，显然δ和θ仅由乘积ωRC决定，关系图如图3-31所示。

图3-31 E、θ 与ωRC的关系曲线

θ的另外一种确定方法：VD1和VD4的关断时刻，从物理意义上讲，就是两个电压下降速度相等的时刻，一个是电源电压的下降速度|du2 /d(ω t) |，另一个是假设二极管VD1和VD4关断而电容开始单独向电阻放电时电压的下降速度 |dud /d(ω t) |p（ 下标表示假设），据此即可确定θ。

3.主要的数量关系

（1）输出电压平均值：

空载时，

重载时，Ud逐渐趋近于0.9U2，即趋近于接近电阻负载时的特性。

在设计时根据负载的情况选择电容C值，使 RC ≥(3~5)T /2，此时输出电压为：Ud ≈ 1.2U2。

（2）电流平均值：

输出电流平均值IR为

（3）二极管电流iD平均值为

（4）二极管承受的电压。

3.4.2 电容滤波的三相不可控整流电路

1.基本原理

电容滤波的三相桥式不可控整流电路及其波形如图3-32所示，某一对二极管导通时，输出电压等于交流侧线电压中最大的一个，该线电压既向电容供电，也向负载供电。当没有二极管导通时，由电容向负载放电，ud按指数规律下降。

图3-32 电容滤波的三相桥式不可控整流电路及其波形

比如在VD1和VD2同时导通之前VD6和VD1是关断的，交流侧向直流侧的充电电流id是断续的。VD1一直导通，交替时由VD6导通换相至VD2导通，id是连续的。由“电压下降速度相等”的原则，可以确定临界条件。假设在 ωt+δ= 2π/3的时刻“速度相等”恰好发生，则有(www.xing528.com)

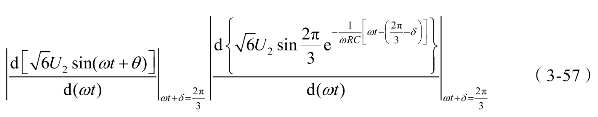
由上式可得电流id断续和连续的临界条件在轻载时直流侧获得的充电电流是断续的，重载时是连续的，分界点就是通常只有R是可变的，它的大小反映了负载的轻重，因此在轻载时直流侧获得的充电电流是断续的，重载时是连续的，ωRC等于和小于时的电流波形如图3-33（a）和3-33（b）所示。

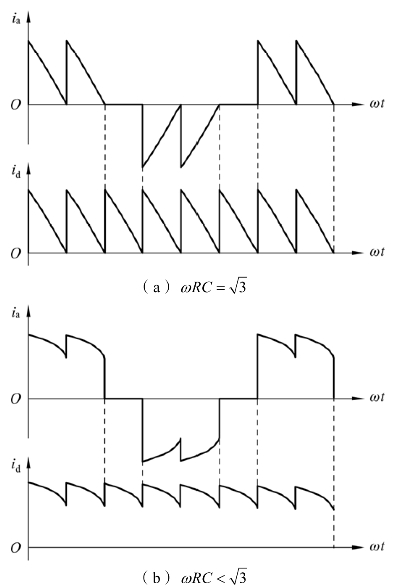
图3-33 电容滤波的三相桥式整流电路当ωRC等于和小于时的电流波形

考虑实际电路中存在的交流侧电感以及为抑制冲击电流而串联的电感时的工作情况：

电路及其波形如图3-34所示，电流波形的前沿平缓了许多，有利于电路的正常工作。随着负载的加重，电流波形与电阻负载时的交流侧电流波形逐渐接近。

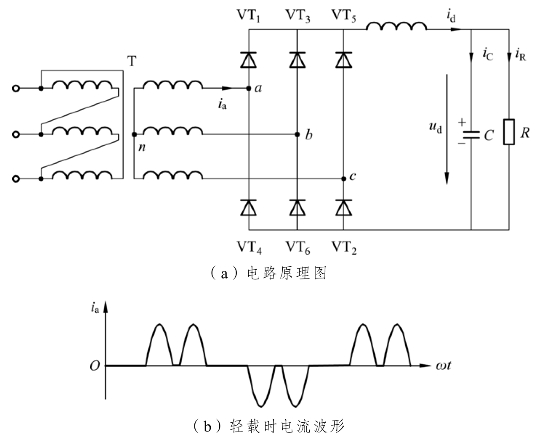
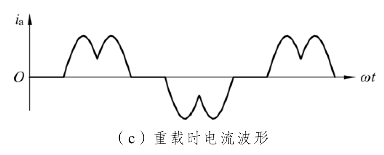
图3-34 考虑电感时电容滤波的三相桥式整流电路及其波形

2.主要数量关系

（1）输出电压平均值Ud在2.354U2～2.45U2之间变化。

（2）输出电流平均值IR为

（3）与单相电路情况一样，电容电流iC平均值为零，因此：Id＝IR。

（4）二极管电流平均值为Id的1/3，即

（5）二极管承受的最大反向电压为线电压的峰值为。

3.4.3 多重联结电路

可采用多重化整流电路减轻整流装置所产生的谐波、无功功率等对电网的干扰，将几个整流电路多重联结可以减少交流侧输入电流谐波，而对晶闸管多重整流电路采用顺序控制的方法可提高功率因数。

移相多重联结，有并联多重联结和串联多重联结。它可减少输入电流谐波，减小输出电压中的谐波并提高纹波频率，从而减小对平波电抗器的要求。

图3-35的电路是两个三相桥并联而成的12脉波整流电路。

图3-35 并联多重联结的12脉波整流电路

1.移相30°构成的串联2重联结电路

整流变压器二次绕组分别采用星形和三角形接法构成相位相差30°、大小相等的两组电压，接到相互串联的两组整流桥。图3-36为该电路为12脉波整流电路。

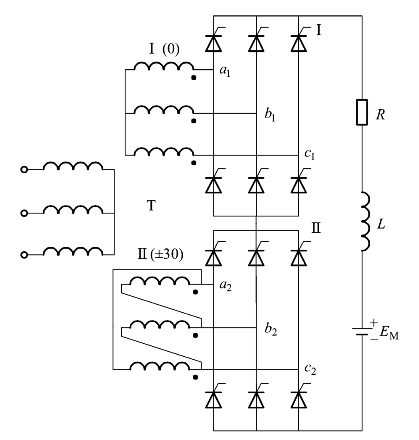
图3-36 移相30°串联2重联结电路

对波形ia进行傅立叶分析，可得其基波幅值Im1和n次谐波幅值Imn分别如下：

即输入电流谐波次数为12k±1，其幅值与次数成反比而降低。其他特性如下：

直流输出电压：

位移因数：

功率因数：

利用变压器二次绕阻接法的不同，互相错开20°，可将三组桥构成串联3重联结电路，整流变压器采用星形三角形组合无法移相20°，需采用曲折接法。整流电压ud在每个电源周期内脉动18次，故此电路为18脉波整流电路。交流侧输入电流谐波更少，为18k±1次（k=1，2，3，…），ud的脉动也更小。输入位移因数和功率因数分别为

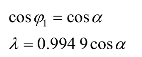
将整流变压器的二次绕组移相15°，可构成串联4重联结电路为24脉波整流电路。其交流侧输入电流谐波次为24k±1，k=1，2，3，…输入位移因数功率因数分别为

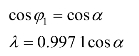
采用多重联结的方法并不能提高位移因数，但可使输入电流谐波大幅减小，从而也可以在一定程度上提高功率因数。

2.多重联结电路的顺序控制

只对一个桥的α 角进行控制，其余各桥的工作状态则根据需要输出的整流电压而定，或者不工作而使该桥输出直流电压为零，或者α＝0而使该桥输出电压最大。根据所需总直流输出电压从低到高的变化，按顺序依次对各桥进行控制，因而被称为顺序控制，单相串联3重联结电路及顺序控制时的波形如图3-37所示。

图3-37 单相串联3重联结电路及顺序控制时的波形

以用于电气机车的3重晶闸管整流桥顺序控制为例，当需要输出的直流电压低于三分之一最高电压时，只对第Ⅰ组桥的α 角进行控制，

同时VT23、VT24、VT33、VT34保持导通，这样第Ⅱ、Ⅲ组桥的直流输出电压就为零。

当需要输出的直流电压为输入交流电压最大值的1/3时，第Ⅰ组桥的α 角为0；需要输出的直流电压值在输入交流电压最大值的1/3到2/3区间内时，第Ⅰ组桥的α 角固定为0，VT33和VT34维持导通，仅对第Ⅱ组桥的α 角进行控制；需要输出的直流电压大于等于输入交流电压最大值的2/3时，第Ⅰ、Ⅱ组桥的α 角固定为0，仅对第Ⅲ组桥的α 角进行控制。使直流输出电压波形不含负的部分，可采取如下控制方法。以第Ⅰ组桥为例，当电压相位为α 时，触发VT11、VT14使其导通并流过直流电流。在电压相位为π 时，触发VT13，则VT11关断，通过VT13、VT14续流，桥的输出电压为零而不出现负的部分。电压相位为π＋α时，触发VT12，则VT14关断，由VT12、VT13导通而输出直流电压。电压相位为2π 时，触发VT11，则VT13关断，由VT11和VT12续流，桥的输出电压为零。顺序控制的电流波形中，正（或负）半周期内前后四分之一周期波形不对称，因此含有一定的偶次谐波，但其基波分量比电压的滞后少，因而位移因数高，从而提高了总的功率因数。