平面立体相交的特性与应用

平面与平面立体相交，其截交线为平面多边形。

（一）平面与棱柱相交

图3-11（a）所示为正五棱柱被正垂面P所截切，其作图步骤如下：

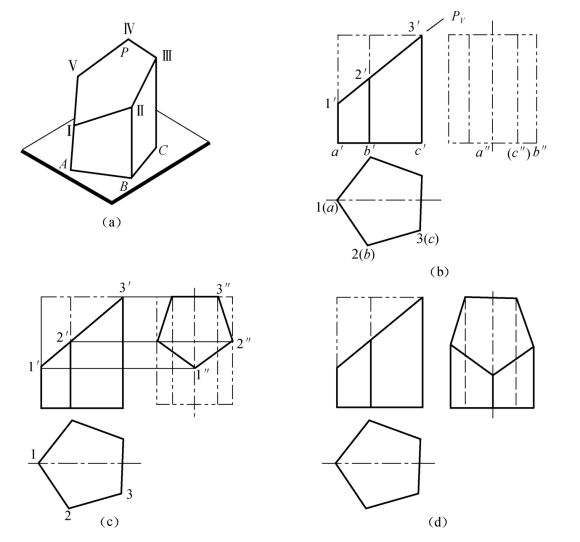
图3-11　平面与正五棱柱相交

（1）画出完整的正五棱柱的3个投影，在正面投影中，五棱柱被平面截去的部分用细双点画线表示，如图3-11（b）所示。

（2）因为截平面为正垂面，所以PV具有积聚性。根据截交线的性质，PV与正五棱柱的所有棱线相交，交点为Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ，如图3-11（a）所示。因此正面投影中的棱线交点1′、2′、3′为截平面与各棱线的交点Ⅰ、Ⅱ、Ⅲ的正面投影。

（3）根据正面投影1′、2′、3′作出其水平投影1、2、3及侧面投影1″、2″、3″，如图3-11（c）所示。

（4）作出对称的另一半，并连接各点的同面投影即得截交线的3个投影。

（5）判断可见性，擦除不必要的图线，并描深全部的图形，如图3-11（d）所示。

图3-12所示为正六棱柱被正垂面P所截切，截交线的正面投影积聚成直线且与截平面的正面投影重合；截交线的水平投影是正六边形且与棱柱的水平投影重合；截交线的侧面投影为与其类似的六边形。根据截交线的正面投影a′、b′、c′、d′、（e′）、（f′）及水平投影a、b、c、d、e、f，即可求出其侧面投影a″、b″、c″、d″、e″、f″，依次连接各点即得截交线的侧面投影。(www.xing528.com)

因为棱柱的左上部被切去，所以，截交线的侧面投影可见。在侧面投影中，点D所在的侧棱投影不可见，故画成细虚线；而细虚线的下部分与可见点A所在的侧棱投影重合，所以画成粗实线，如图3-12（b）所示。

图3-12　作正六棱柱的截交线

（二）平面与棱锥相交

如图3-13（a）所示，正三棱锥S-ABC被正垂面P所截切，其作图步骤如下。

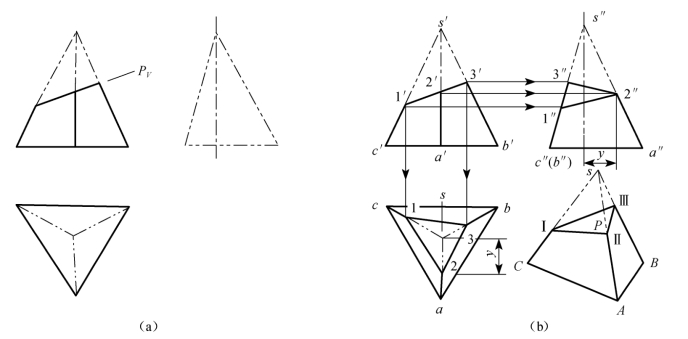
图3-13　平面与正三棱锥相交

（1）因为截平面为正垂面，所以PV具有积聚性。根据截交线的性质，PV截平面与各棱线的交点Ⅰ、Ⅱ、Ⅲ的正面投影为s′a′、s′b′、s′c′上的投影点1′、2′、3′。

（2）根据正面投影1′、2′、3′作出其水平投影1、2、3及侧面投影1″、2″、3″。

（3）连接各点的同面投影即得截交线的3个投影。

（4）判断截交线的可见性。因为被截立体为正三棱锥，所以截交线均可见，结果如图3-13（b）所示。