破碎机振动力的数学模型优化

破碎机是用于破碎石料和矿石的机械设备，如图9-25a所示。它由曲柄AB、动腭BC及推力板CD组成。当曲柄转动时，动、定腭之间的空间往复大小改变，以达到破碎和排料的目的。将推力板的表面做成圆弧状，其与动腭和机架的凹槽为线接触，使机构运转时呈滚动以减小功耗，且方便更换。机器运转时，由于动腭的质量很大（推力板质量相对很小）且为变速运动，产生较大的惯性力和惯性力矩，使机器产生振动。

为分析方便，将破碎机简化为如图9-25b所示的铰链四杆机构。由于破碎机这种特殊的推力板结构（无法另加配重），只能在曲柄的反向加配重以平衡机座上的振动力。传统的方法是按质量静替代在与曲柄同轴的飞轮上，沿曲柄反方向装加附加质量m′。其方法为：先将m₂用质量静替代方法分解到曲柄上，然后在曲柄的反向用质量m′加以平衡。其计算式：

该平衡方法不尽合理，首先式（9-56）只适用于不平衡质量m₂位于连杆BC的轴线上的情况；其次该平衡质量m′不能平衡垂直曲柄方向的振动力。故提出如下破碎机振动力最优平衡方法（如图9-25c、d所示）：

1）在机构运动分析的基础上求出动腭的惯性力F₂和惯性力矩M₂。

2）根据达朗贝尔原理将惯性力和惯性力矩视为外力加于动腭上（图9-25c），按静力学方法求出支座A的振动力（也称附加动压力）R_1x、R_1y。

3）用优化方法使得在运动周期内振动力R_1x、R_1y的最大值极小，从而求出配重的大小和方位m_b、α_b。

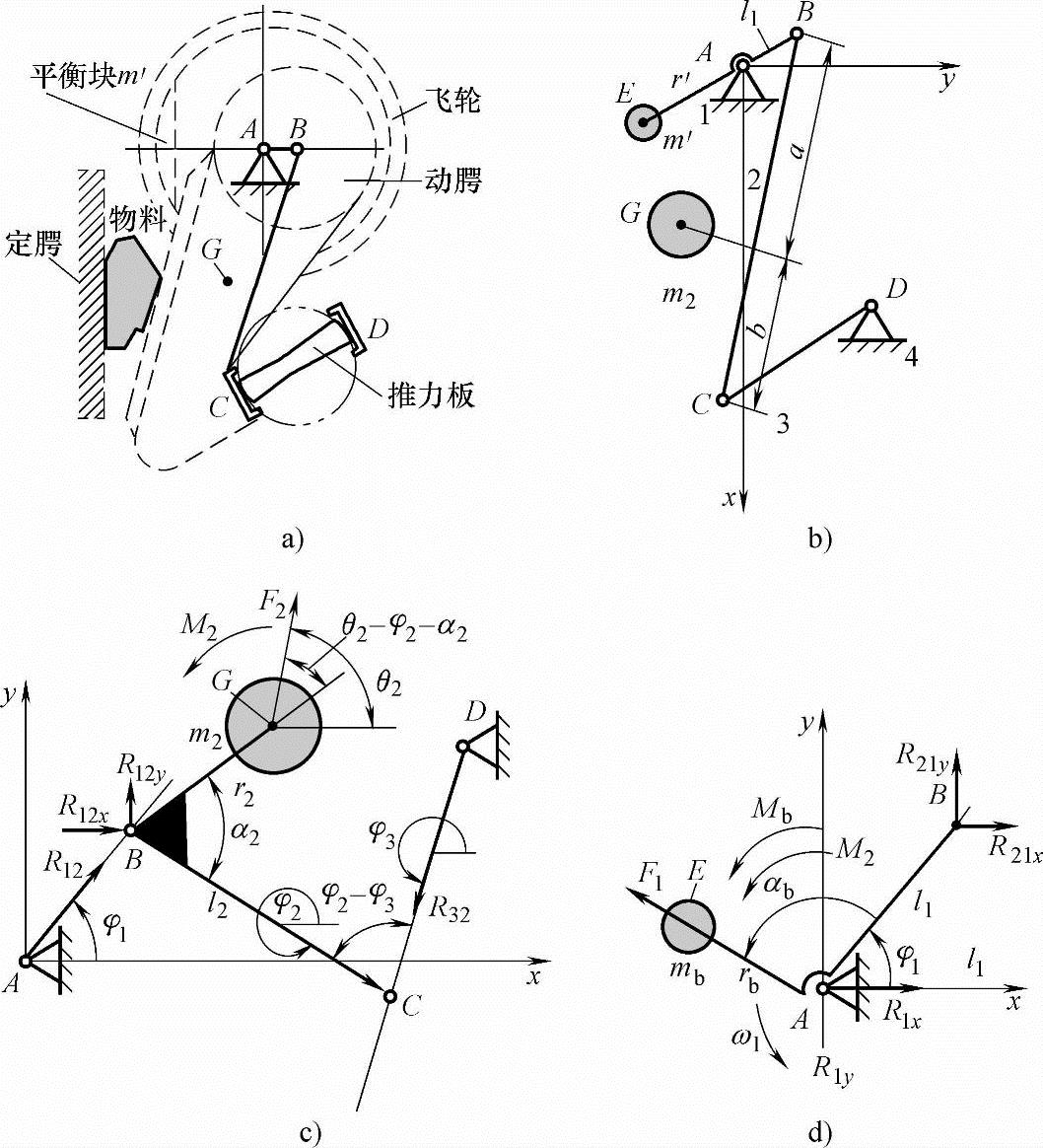
图9-25 破碎机及其机构分析

按照第2章提供的方法进行机构运动分析，求出构件2（动腭）的位置角φ₂、角速度ω₂、角加速度ε₂、动腭重心处的加速度a_G及其方向角β_G。由力学及几何关系得

式中，J_G是动腭对质心G的转动惯量。

求出动腭的惯性力F₂、惯性力矩M₂，并视为外力加于动腭上。此时动腭在外力和运动副反力作用下处于平衡状态。求动腭上各力对B点的力矩，得

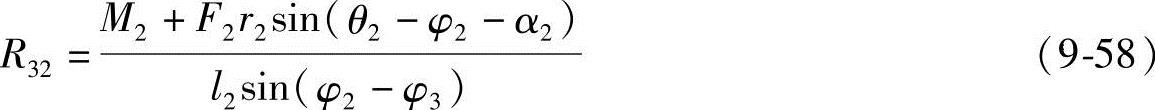
由∑x=0，∑y=0得

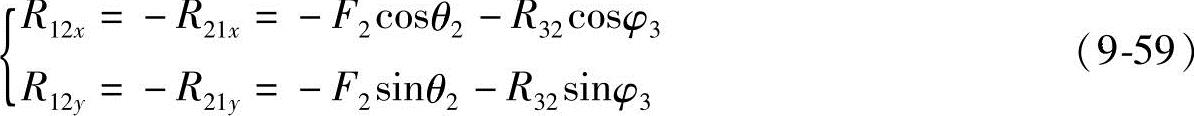(www.xing528.com)

如图9-25d所示，为使动腭对曲柄作用在机座上的附加动压力得以平衡，加一个附加质量m_b，其向径为r_b，位置角为φ₁+α_b。由于曲柄等速转动，故惯性力矩M₁=0，其离心力为：

F₂=m_br_bω²₁ （9-60）

作用在曲柄上的平衡力矩M_b及机座A上附加动压力R₁为：

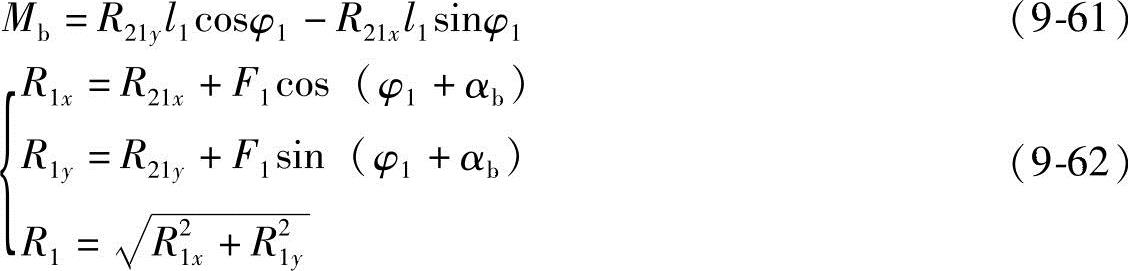
曲柄上的力矩M_b将由原动机平衡，而动压力R₁就是使机器产生振动的原因。最优动力平衡的目的就是通过调整附加质量的大小和位置使剩余附加动压力减小到最小值。

设计变量：X=（m_bα_b）^T （9-63）

目标函数有两种形式：

1）以剩余附加动压力最大值极小为目标函数。

minF₁（X）=min（R_1max） （9-64）

2）以剩余附加动压力在一个运动循环中的均方根值极小为目标函数。

约束条件：

式中，k为给定系数。