综合方法优化单控件五杆机构

单控件五杆机构的综合模型可以采用不同的综合方法。一般采用先四杆后五杆的两步综合法和Ⅱ级杆组综合法。

如图9-22a所示，曲柄AB和滑块3是主动件，其中滑块3为受控主动件，要求该机构M点精确实现轨迹y_i=f（x_i） （i=1，2，…，n）。

1）两步综合法。先用最优综合的方法综合出一个起始四杆机构ABCD（去掉受控件3）。该四杆机构能在尽可能多的点位上最优近似地逼近给定运动。再在起始四杆机构的基础上，引进受控主动件（滑块3），并按照给定的M点的坐标值计算受控主动件的补偿位移s₃（φ_1i），从而精确实现任意给定运动。

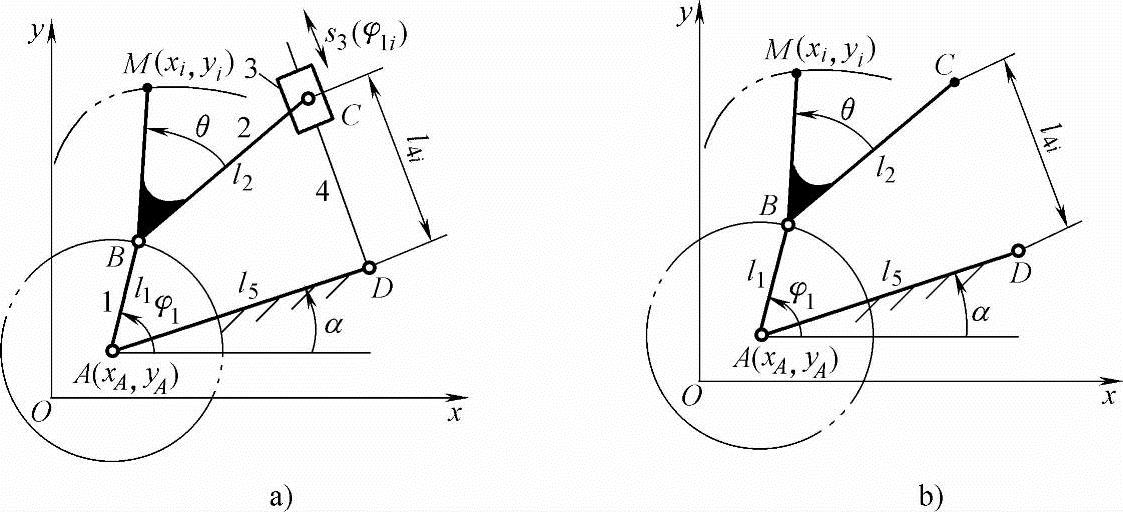
图9-22 单控件五杆机构综合模型(www.xing528.com)

a）单控件五杆机构 b）Ⅱ级杆组综合模型

2）Ⅱ级杆组综合法。设将构件3、4从机构中拆下，如图9-22b所示。将Ⅱ级杆组ABC上的转动副装于机架上的A点，使点M沿轨迹M（x_i，y_i）运动的同时，曲柄AB绕A点作圆周运动。此时C点到D点的距离l_4i将随曲柄转动而发生变化。以l_4i变化极小为目标进行机构优化，求出各尺寸参数及l_4i的变动值Δl_4i，受控主动件的补偿位移s₃（φ_1i）=Δl_4i。

由于单控件五杆机构只有一个受控驱动系统，因此与双控件五杆机构相比，其成本低廉。但由于非是受控主动件的运动不能调整，且机构尺寸参数已经固定，只能实现某一特定的运动规律。