【摘要】：除满足给定函数要求外，还可考虑机构的传力特性。由于四杆机构两连架杆对应转角与机架AD的位置和各杆长绝对值无关，因此取x轴与机架AD重合，并令AD=d=1，a、b、c均为相对尺寸。，n所有位置的偏差极小来建立：图9-15 铰链四杆机构连架杆对应转角由铰链四杆机构的几何关系可导出输出构件转角φ3i与输入构件转角φ1i的关系：φ3i=f 机构优化的目标函数可按式与给定函数φ3i=f（φ1i）在i=1，2，…
在实际工程中，往往遇到连杆上M点要求沿给定轨迹运动，同时又要求连杆按给定的角位移运动。即要求M点按给定轨迹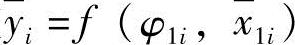
、连杆按给定角位移
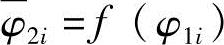运动的机构最优设计问题（图9-19）。该设计问题的目标函数可用再现轨迹和再现连杆角位移两个目标线性加权方法来建立。即
F（X）=W1F1（X）+W2F2（X） （9-44）
式中，F1（X）和F2（X）分别为再现轨迹和连杆角位移的目标函数；W1和W2为加权因子，其值决定于两项目标的数量级及其重要程度。
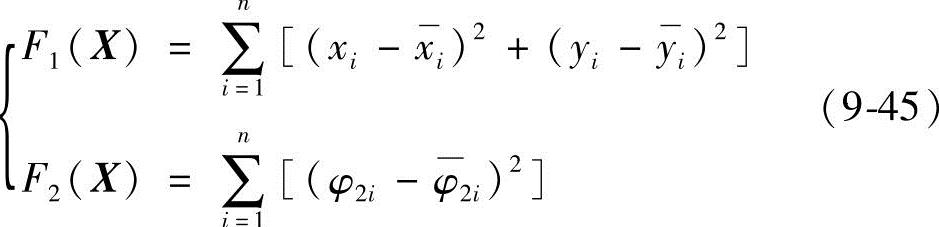
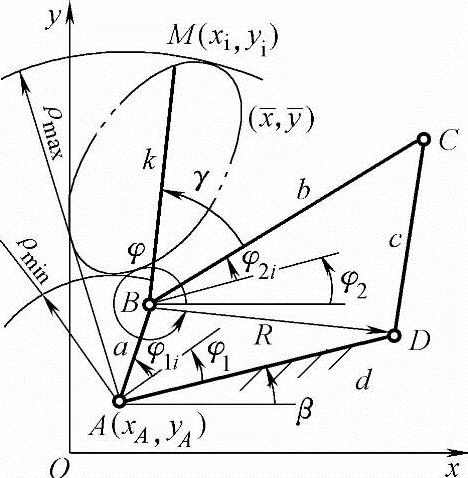
图9-19 连杆机构实现刚体导引
设计变量有机架位置参数xA、yA、β，机构尺寸参数a、b、c、d、M点的位置参数k、γ及输入构件AB的初位置角φ1。如果输入构件各转角φ1i也为变量，则设计变量（i=1，2，…，n）共有n+10个。如前所述，当A点坐标xA，yA确定后，则尺寸a，k是xA，yA及M点给定位置坐标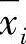
，
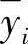的函数。(https://www.xing528.com)
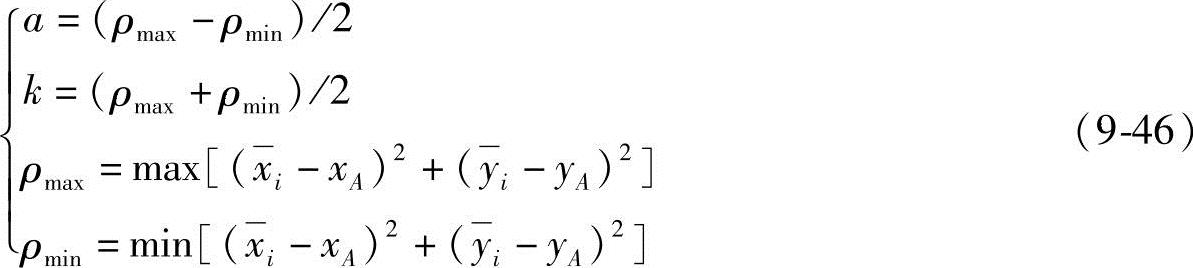
设计变量将减少两个。
式（9-45）中φ2i及M点再现的坐标值xi，yi分别为
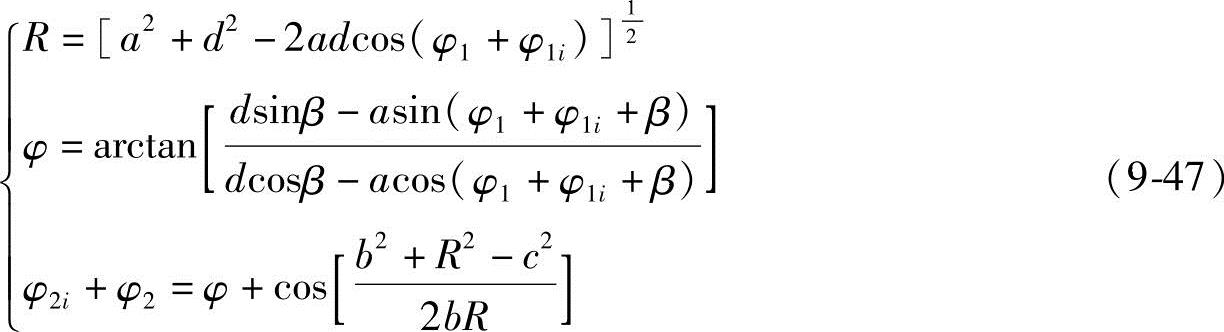
当φ1i=0时φ2i=0，通过式（9-47）可计算出φ2。
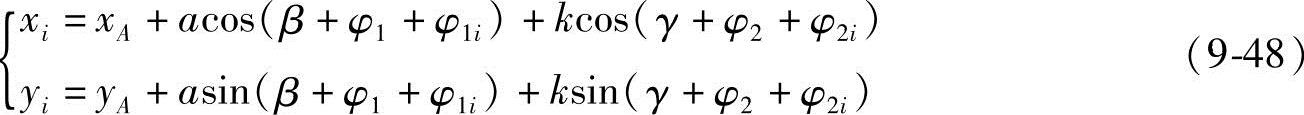
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
