带滑块的六杆Ⅲ级机构的可动性条件

如图9-9所示为带一个滑块、带两个滑块和带三个滑块的具有代表性的Ⅲ级机构的典型结构。图9-9c所示带三个滑块的六杆Ⅲ级机构中有曲柄的条件与机构尺寸无关。现分别讨论图9-9a、b所示两种情况的机构有曲柄条件。

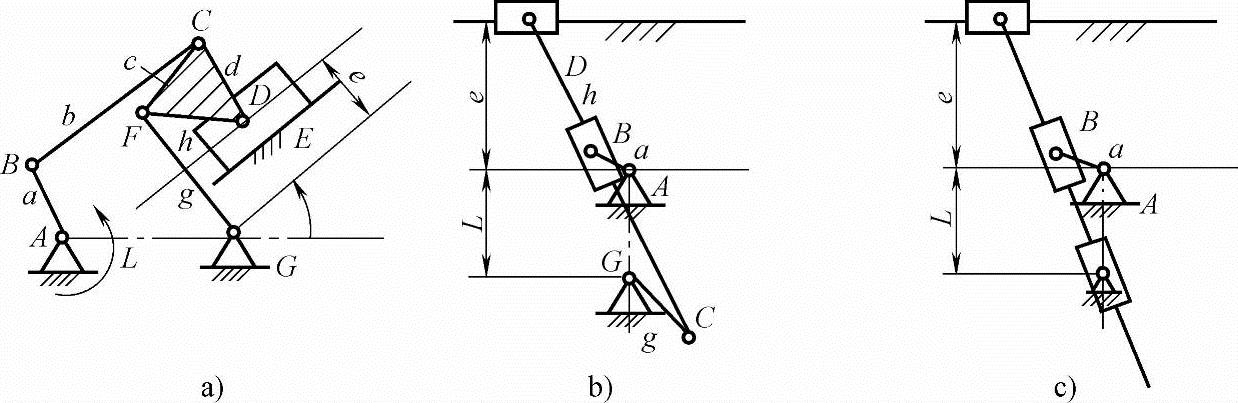
图9-9 Ⅲ级机构的典型结构

1.带一个滑块的六杆Ⅲ级机构的有曲柄条件

如图9-9a所示机构若将GF改为主动件则得到如图9-10a所示的六杆Ⅱ级机构。该六杆Ⅱ级机构由带滑块的四杆机构GFD与Ⅱ级杆组ABC构成（构件AB、BC用虚线画出）。

如图9-10b所示为四杆机构GFD的两个极限位置。杆长h（一般g＞h）应满足

h≤g-e （9-21）

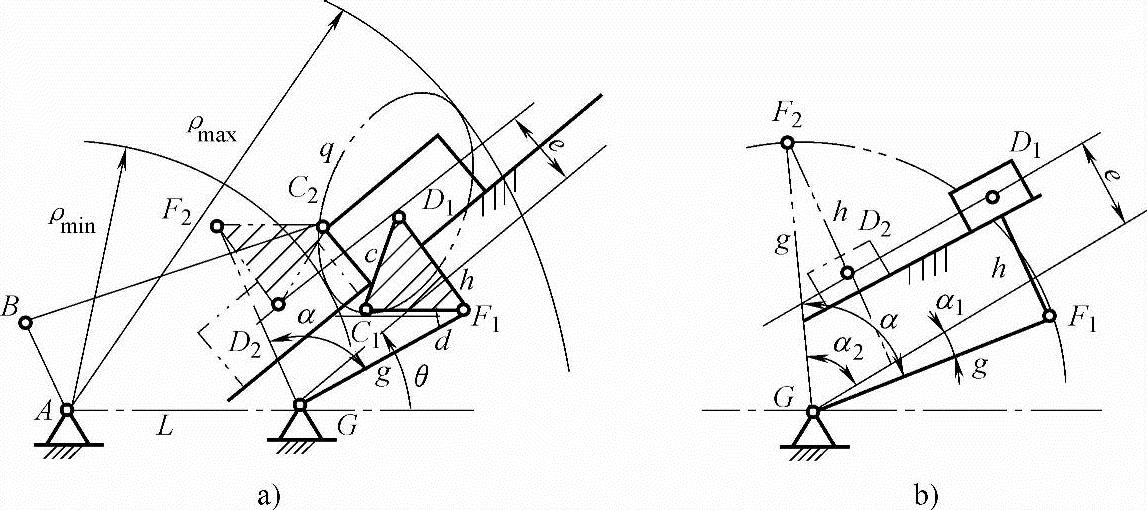
图9-10 一个滑块的六杆Ⅱ级机构

构件GF的极限摆角α=α₁+α₂=arcsin[（h-e）/g]+arcsin[（h+e）/g]，对四杆机构GFD进行运动分析求得点C的轨迹q。最后计算出支座A距该轨迹最远、最近距离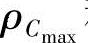和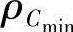。则原六杆Ⅲ级机构中AB、BC的尺寸为

例9-5 如图9-10所示已知L=100，d=c=40，e=20，g=80，θ=60°。求带一个滑块的六杆Ⅲ级机构满足AB为曲柄时，杆长a、b、h的大小。

解：由式（9-21）得

h≤g-e=60

取h=40，求得杆GF的摆角范围为45.5225°～108.5904°。将该摆角均分为180等分计算F点往复运动的360个点位的C点位置后得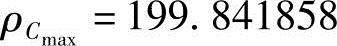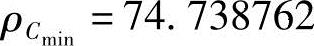，。由式（9-22）得

b=137.290314，a≤62.551548

然后可依前述方法，利用计算机计算有曲柄条件。程序如下：(www.xing528.com)

运算过程及结果

L=100.000000，g=80.000000，d=40.000000，h=40.000000，e=20.000000，sida=60.000000，

sidad=60.000000 （注：打印已知参数）

faia=14.477524，faib=48.590420，dtafai=0.350377 （注：打印GF杆的摆角α及n分度角）

lmax=199.841858，lmin=74.738762，la=62.551548，lb=137.290314 （注：打印C点最大、最小向径即a、b的数值）

2.带两个滑块的六杆Ⅲ级机构的有曲柄条件

图9-9b所示为以AB为主动件的Ⅲ级机构，若将滑块D变换为主动件后，得到如图9-11所示的Ⅱ级机构（其中的二杆组AB用虚线绘出）。已知机架尺寸L、e及GC的杆长g，可以确定杆长h及原六杆Ⅲ级机构的曲柄半径a。图9-11所示GC₁D₁、GC₂D₂为四杆机构DCG的极限位置，由于滑块D可通过中垂线作对称往复运动，故应满足如下关系：

h=e+L+g （9-23）

此时，曲柄半径应保证滑块在极限位置内运动。由极限位置的几何关系得曲柄AB的尺寸：

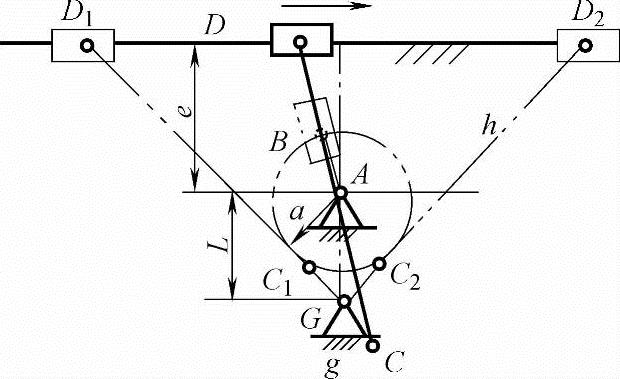
图9-11 Ⅱ级机构

例9-6 如图9-9b所示的Ⅲ级机构中，已知L=100，e=80，g=50，求满足该Ⅲ级机构AB构件为曲柄时的杆长a和杆长h。

解：按式（9-23）得h=e+L+g=230。由式（9-24）得a≤76.5986。此时a的取值可保证滑块在其极限运动区域内运动，否则运动出现干涉。