K≠1曲柄摇杆机构的最佳尺寸组合

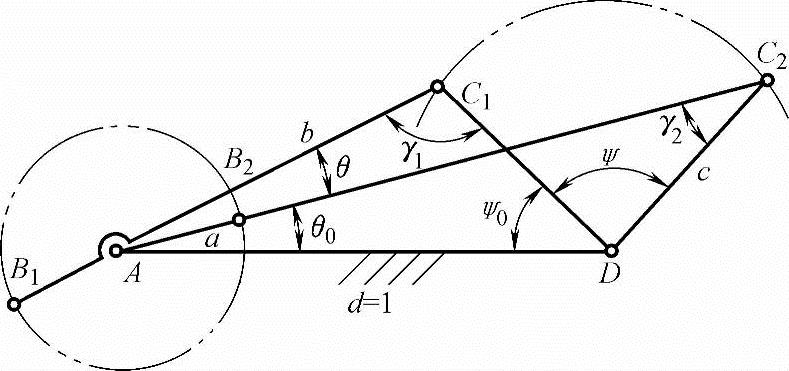
图8-15 K≠1曲柄摇杆机构

如上节图8-8所示，只要已知行程速度变化系数K、摇杆摆角ψ及机构远极位传动角γ₂，按式（8-20）～式（8-22）就可解出机构全部尺寸d=1、a、b、c。优化设计时，行程速度变化系数K和摇杆摆角ψ按生产工艺确定，作为设计常量；机构远极位传动角γ₂作为设计变量。

如图8-15所示，K≠1的曲柄摇杆机构大多用于传递动力。因此，该机构的优化综合应保证整个运动循环中具有最佳的传力性能，即机构的最小传动角最大。另外，为使其具有较大的输出力矩，应尽量增加输出构件摇杆的长度。但也应避免因相对尺寸过分悬殊而加大机构的绝对尺寸。可使摇杆长度c逼近机架长度d。

故目标函数为

minF（γ₂）=min[W₁（90°-γ_min）+W₂|（1-c）|] （8-37）

约束条件：

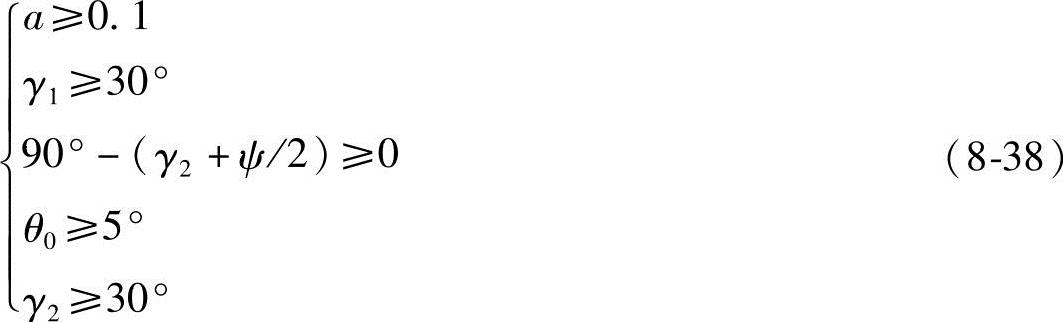(www.xing528.com)

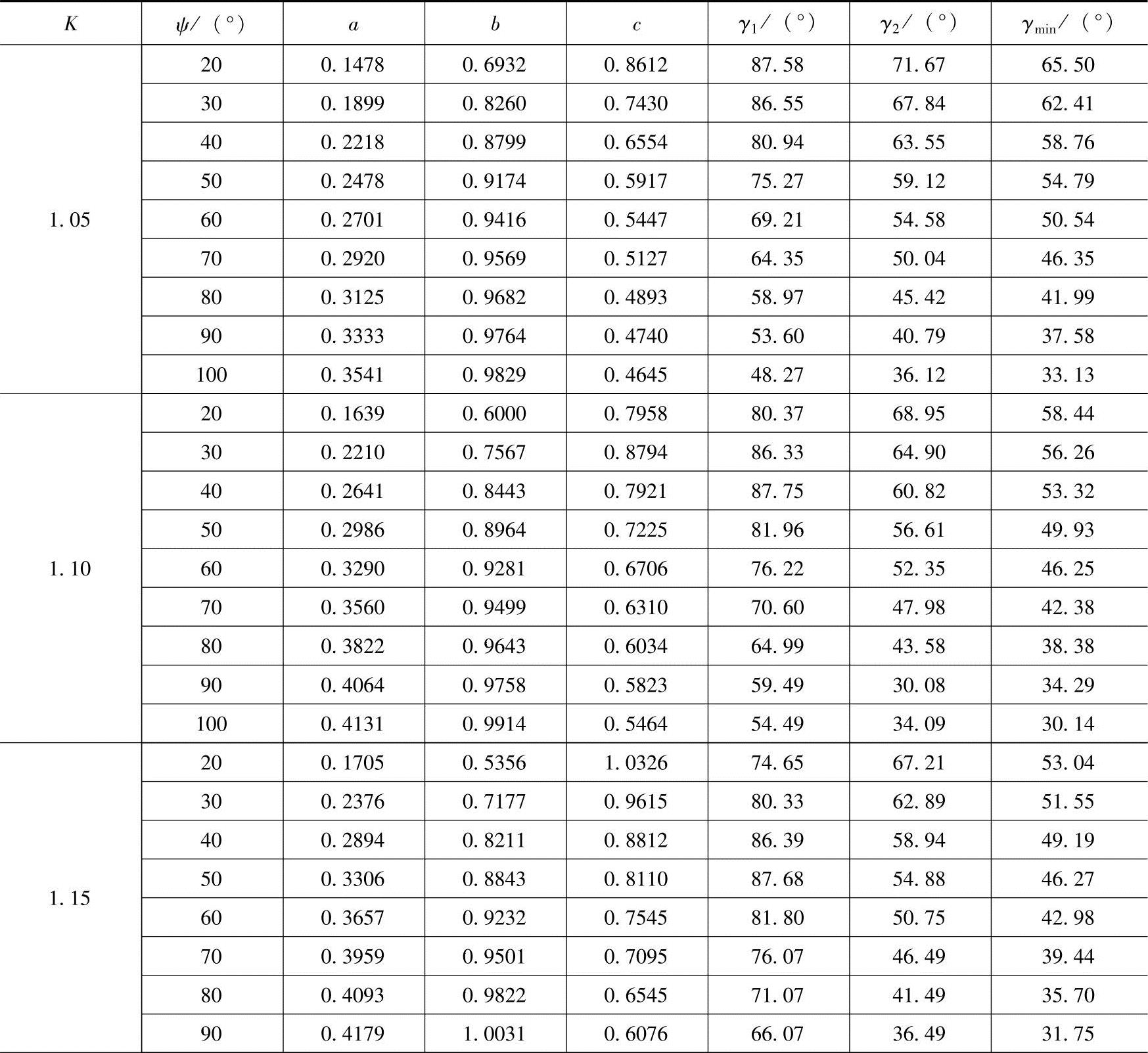
式（8-38）为参数的边界约束和几何约束。其中90°-（γ₂+ψ/2）≥0是考虑曲柄支座A不能在C₁C₂的运动范围之内。d=1的优化结果列于表8-10，设计时可直接选用。

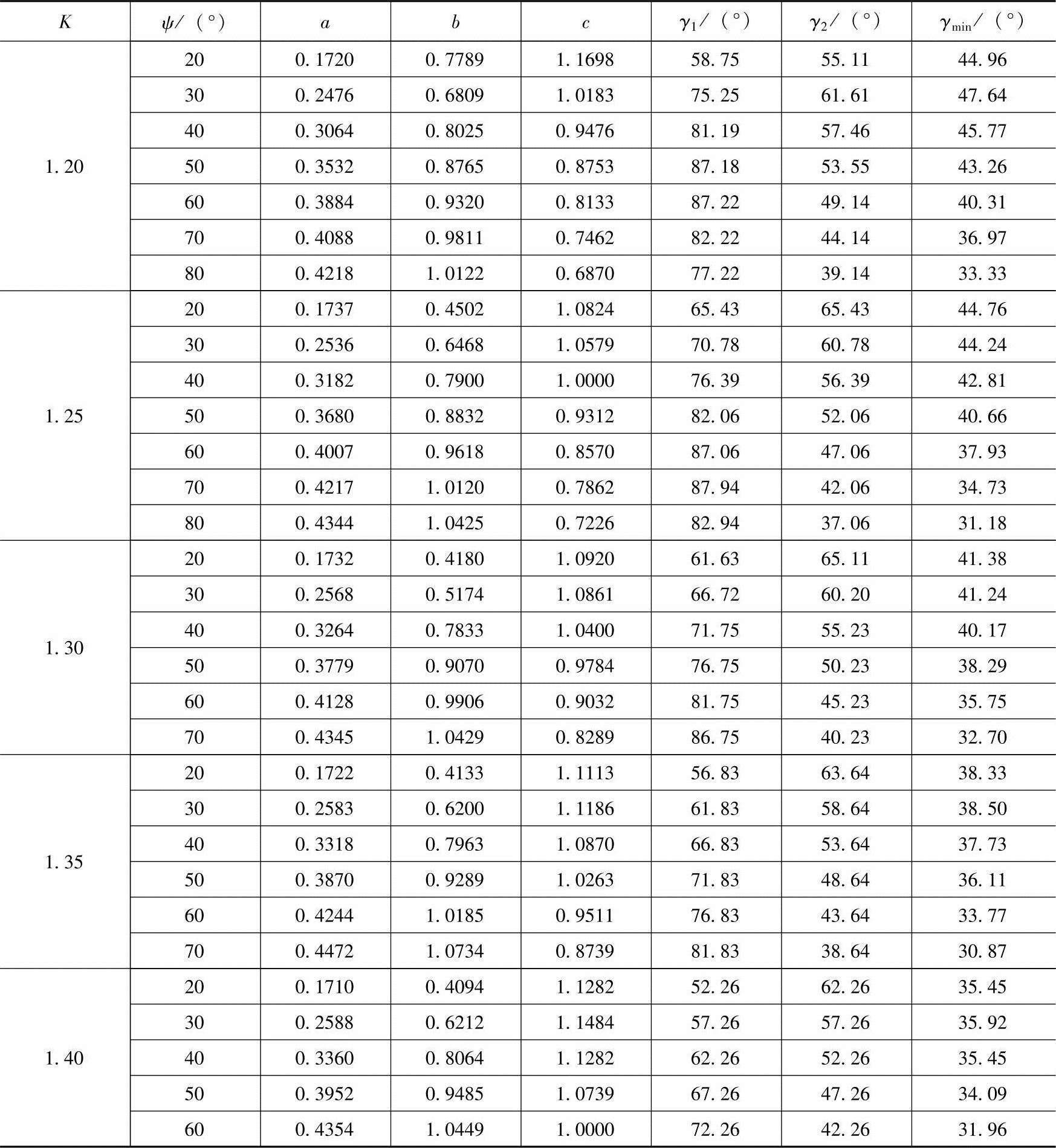
表8-10 K≠1的曲柄摇杆机构最优尺寸族

（续）

四杆机构尺度综合一般采用三维或五维（连架杆初位角也为变量时）优化求解。本节应用机构设计的代数方程采用一维优化求解，此法简明快捷，可供工程实际设计时参考使用。由于工程条件的多样性使得综合的目标函数不尽相同，如摆块机构设计有时要求输出力矩满足某一函数，曲柄摇杆机构有时要求两个极限位置具有最佳传力性能。但根据本节提供的方法，不难重新建立数学模型得到符合实际要求的最佳设计结果。