四杆机构设计：以两连架杆为基准

1.铰链四杆机构

如图8-5所示，已知两连架杆预期所对应转角φ_i、ψ_i（i=1，2，…，n），试设计该四杆机构。由于实现连架杆对应位置与杆长绝对值无关，故图中a、b、c、d均为相对尺寸。α，β分别为两连架杆的初位角。已知d=1，机构待定参数a，b，c，α，β共5个，为得到其精确唯一解应列出五个方程，即连架杆对应位置n=5，当α，β已给定时，机构待定参数3个，只能实现两连架杆三个对应位置。

由环路ABCD得矢量方程：a+b=d+c其投影方程式为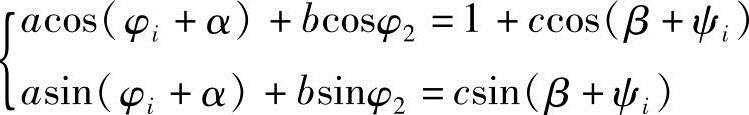（i=1，2，3，…，n）上式消去φ₂得到

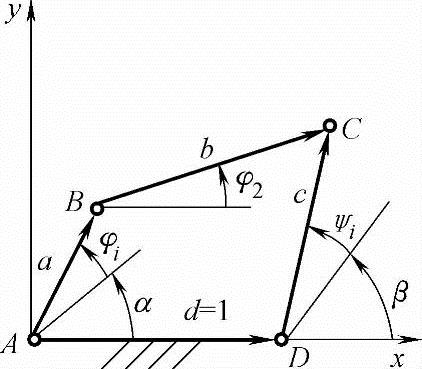
图8-5 按两连架杆对应位置的机构综合模型

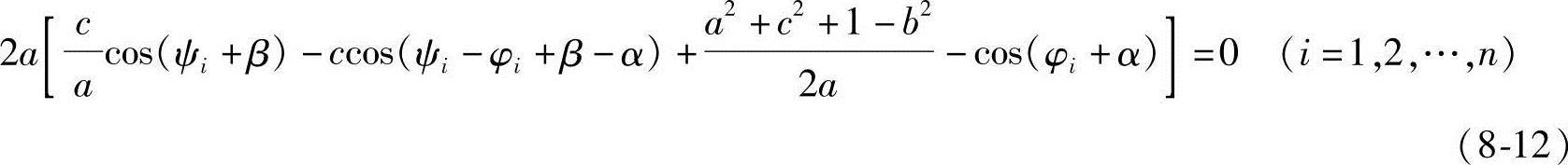
若α，β为给定值，求a、b、c，则式（8-12）可写成如下广义多项式形式

p₀cos（ψ_i+β）+p₁cos（ψ_i-φ_i+β-α）+p₂=cos（φ_i+α） （i=1，2，3，…，n）（8-13）

式中

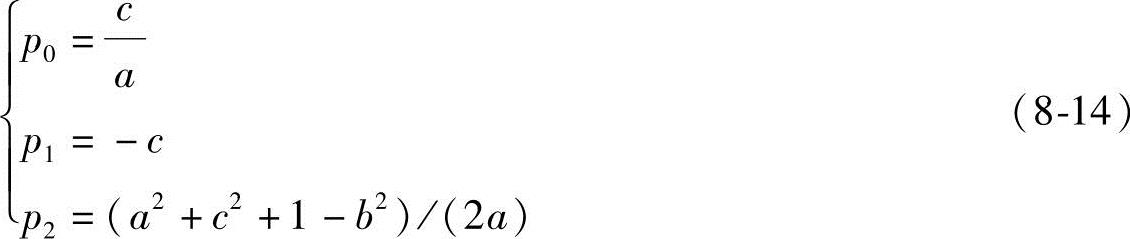
式（8-13）为含有三个待求量p₀、p₁、p₂的线性方程组，将ψ_i、φ_i（i=1，2，3）分别代入式（8-13）中，可求出p₀、p₁、p₂，再由式（8-14）计算出a、b、c。

应该指出若α、β也为待求量，则未知参数为5个：a，b，c，α，β。此时应将式（8-14）中变换的三角函数项展开，并简化为p₀cosφ_i+p₁sinφ_i+p₂cosψ_i+p₃sinψ_i+p₄-（p₀p₂+p₁p₃）cos（ψ_i-φ_i）-（p₀p₃-p₁p₂）sin（ψ_i-φ_i）=0（i=1，2，3，…，n）

（8-15）

式中

式（8-15）是p_j（j=0，1，2，3，4）的非线性方程组，求解比较麻烦，可采用牛顿-拉普森（Newton-Raphson）法求解。

例8-1 如图8-6所示，要求在φ_i=0°～180°范围内两连架杆实现对应转角：ψ_i=30sinφ_i （i=1，2，3，…，n）。初位角α=101.2°，β=29.4°。设d₀=1，要求按零值公式确定三个点位，用代数综合法求机构相对尺寸a₀，b₀，c₀；或按平方逼近法取180个点位，求机构相对尺寸a₀、b₀、c₀。

解：用代数综合法求解时，将式（8-13）写成矩阵式：

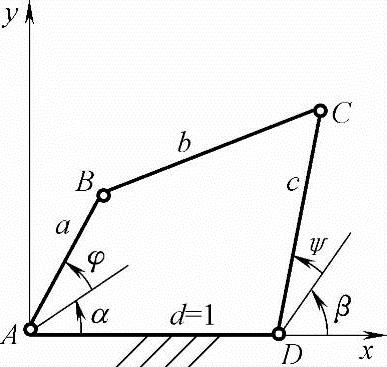
图8-6 按连架杆对应位置设计机构模型

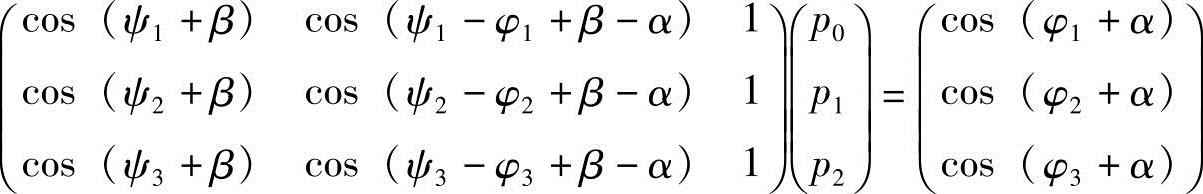(www.xing528.com)

代入已知量求解即可。

用平方逼近法求解时，将式（8-3）、式（8-8）、式（8-9）写成矩阵式：

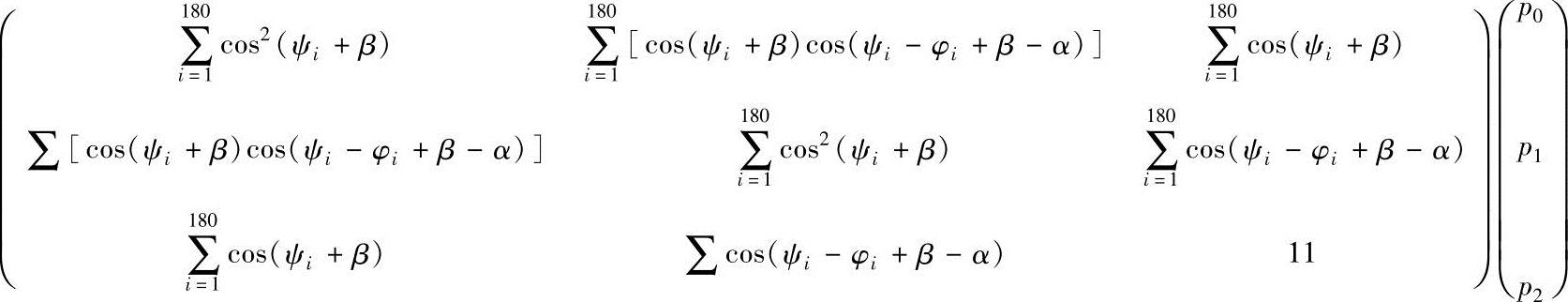
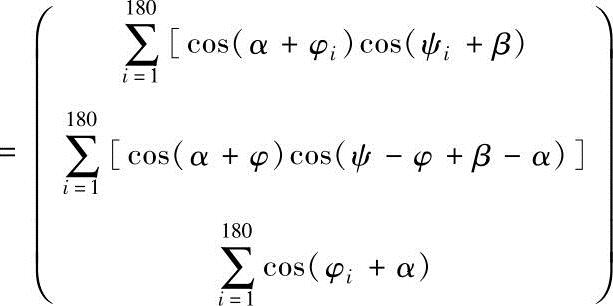
代入已知量求解即可。两种解法的计算机程序如下，可供参考。

按上述两种方法得到的机构尺寸验算一个点位的运动精度，如取φ=90°时，ψ=30°sin90°=30°。按代数综合法计算尺寸得ψ=28.027°；按平方逼近法计算尺寸得ψ=30.4478°。两者的相对误差分别为6.6%和1.5%。

2.曲柄滑块机构

对于曲柄滑块机构，如图8-7所示。已知φ_i、s_i（i=1，2，3）三对应位置。由环路ABCD可得矢量方程a+b=s+e，其投影方程为

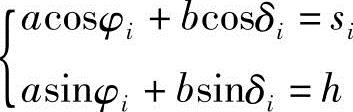
将上式平方相加消去δ_i，经整理后得

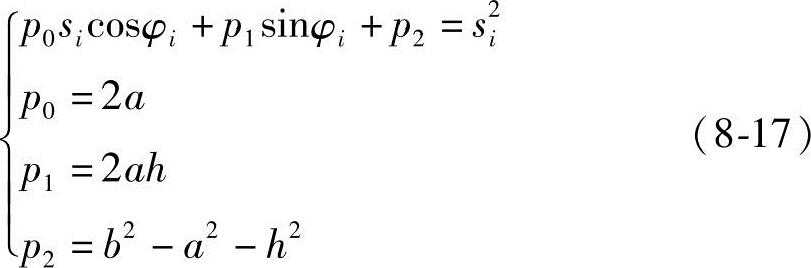
将φ_i，si（i=1，2，3）代入式（8-17），先求出p₀、p₁、p₂，即可计算出a、b、h。

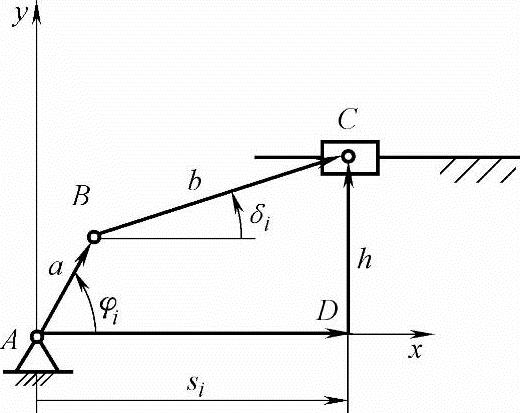
图8-7 曲柄滑块机构对应位置的机构综合模型

应该指出，当构件AB的初位置角φ₀、滑块C的初位移s₀也为待求量时，将得到待求量为a、b、h、φ₀、s₀的五元非线性方程组，可采用Newton-Raphson法求解。此处不再累述。