如图8-2a所示,要求铰链四杆机构实现已知的给定函数ψ=Q(φ),机构能实现的函数ψv=P(a,b,c,α,β,φ),ψv是机构的相对尺寸a、b、c、(d=1),连架杆初位角α、β及自变量φ的函数。对给定函数的偏差为
Δψ=P(a,b,c,α,β,φ)-Q(φ)
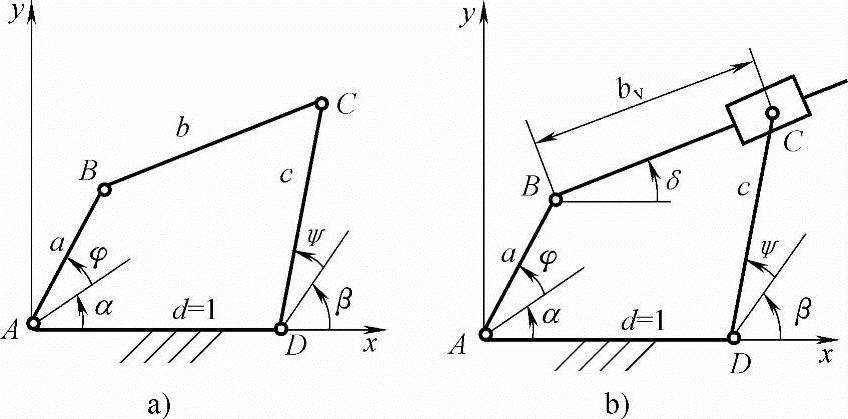
图8-2 按连架杆对应位置设计机构模型
按该式求解机构的尺寸参数是很困难的。为此将四杆机构转换为如图8-2b所示的五杆机构,它是在四杆机构的连杆上引入一个滑块,其自由度为2的机构模型。两连架杆均为输入构件,故AB和DC可以完全精确地实现给定函数ψ=Q(φ)的运动规律,但bv为变量。当该变量与四杆机构的连杆长度b的差值Δb=b-bv很小时,Δψ也很小。根据式(8-2)有加权偏差Δq=qΔψ,因为Δψ很小时Δb也很小,故可以用Δb的加权偏差来表示:
Δq=qΔb
选择q=b+bv≈2b,则加权偏差为Δq=b2-b2v。现讨论如何求出该机构的加权偏差解析表达式。由图8-2b可写出矢量方程AB+BC=AD+DC的坐标方程:
acos(α+φ)+bvcosδ=1+ccos(β+ψ)
asin(α+φ)+bvsinδ=csin(β+ψ)
将以上两式消去δ得
bv=1+c2+a2+2ccos(β+ψ)-2accos(ψ-φ+β-α)-2acos(α+φ)(https://www.xing528.com)
由此得
Δq=2accos(ψ-φ+β-α)+2acos(α+φ)-2ccos(ψ+β)+b2-a2-c2-1(8-1)
在求解机构的三个参数时,可把式(8-1)展开后各项加以归并得到如下广义多项式的形式:
Δq=A[p0f0(φ)+p1f1(φ)+p2f2(φ)-Q(φ)] (8-2)
式中,p0,p1,p2是机构待求参数或待求参数的函数;f0(φ),f1(φ),f2(φ),Q(φ)是由给定函数的参数确定的已知表达式,它们随所求参数的不同而有不同的组合形式。
若初位角α,β已知,求机构参数a,b,c时,由式(8-1)、式(8-2)得
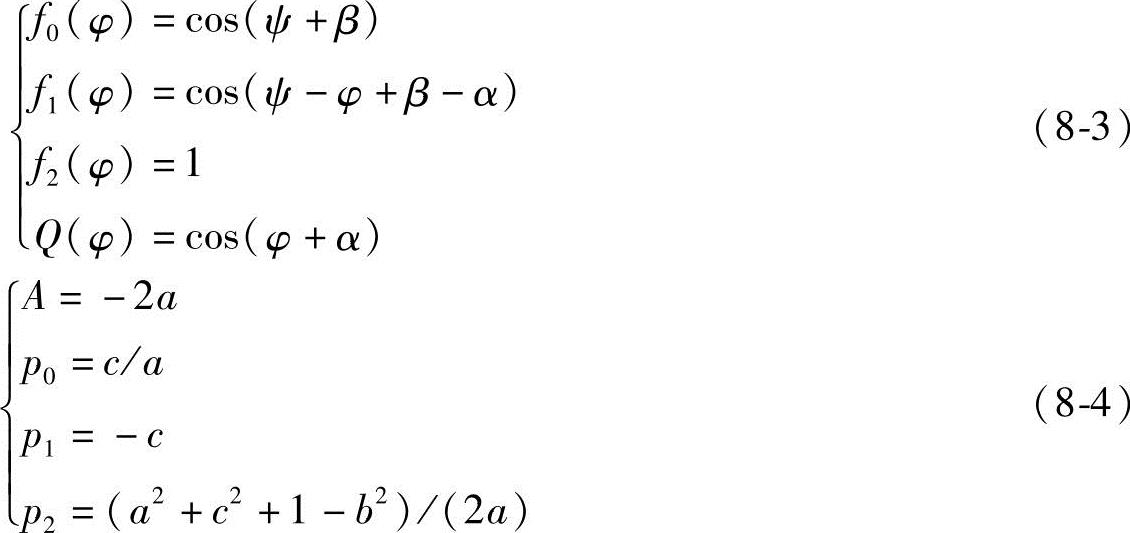
若c,β已知,求a,b和α时,有
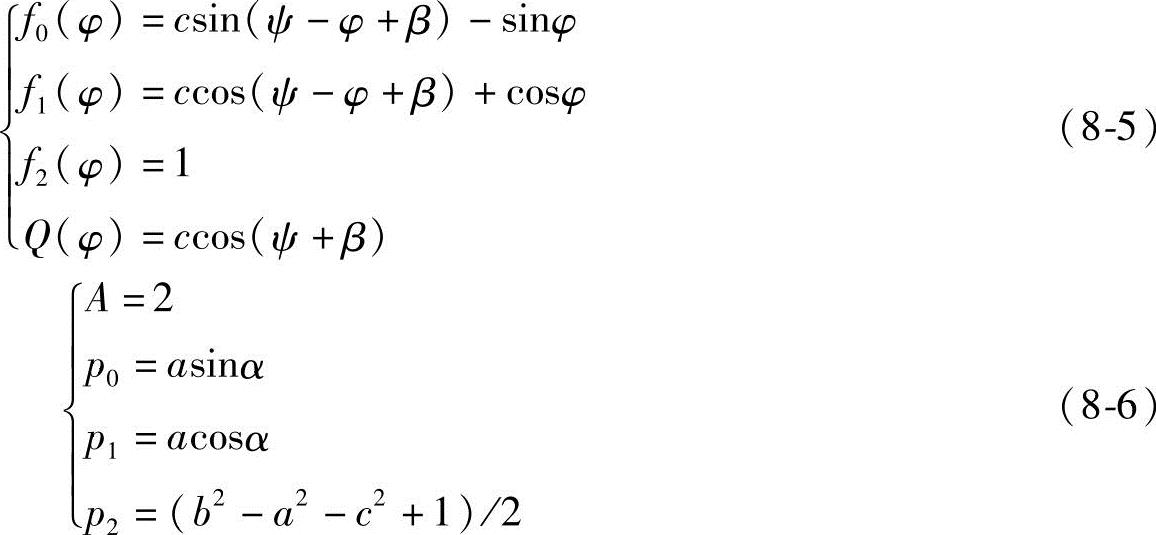
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




