优化机构中的加权偏差解析式

如图8-1所示，要求机构实现的给定函数为y=F（x），机构上某点能够实现的函数为yp=F_p（x），称为逼近函数。机构综合的目的就是要确定机构的全部或部分尺寸参数，使得机构能实现的逼近函数y_p=F_p（x）在自变量区间[x_ax_b]内与给定函数y=F（x）的差值很小。该差值称为对给定函数的偏差Δy。

Δy=y_p-y=F_p（x）-F（x）

机构参数能否方便求解，在很大程度上取决于如何选择给定函数的偏差解析式。即使对于简单的四杆机构，其偏差解析式往往也是十分复杂的。因此，一般不采用真正的偏差Δy，而采用其近似表达式或加权偏差Δq=qΔy。只要q在自变量区间内不为零，且近似于某常数，则Δq可以表示Δy的变化特性，q称为权。当q选择合适时加权偏差Δq的解析式将大大简化。当权不但是自变量的函数而且也是机构参数的函数时，加权偏差Δq的表达式可以更为简化，该权称为参数权。

例如，给定函数y=b是一条与x轴平行的直线。而机构能实现的函数为

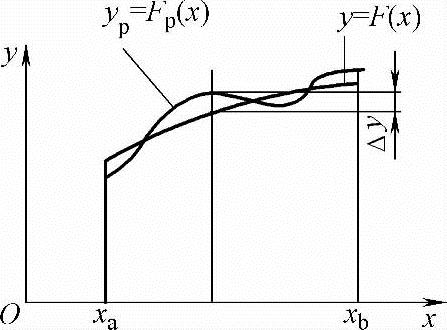
图8-1 函数偏差

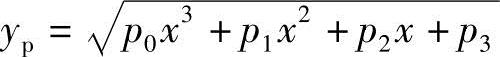(www.xing528.com)

式中，p₀，p₁，p2，p3是机构的待定参数。

对给定函数的偏差为

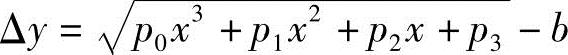
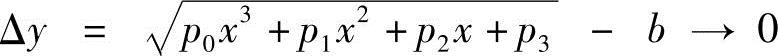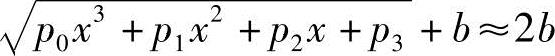由于Δy求解困难，采用加权偏差Δq=qΔy来代替对给定函数的偏差。q应满足不为零，且近似于某常数，例如当时，令。则有

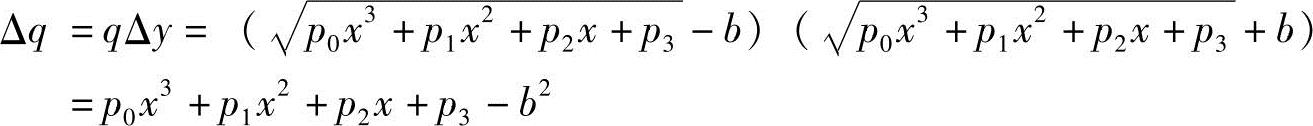
这样，使Δq→0来求解机构的待定参数就简单多了。