用复合形法解约束优化问题的源程序

例7-2 用复合形法求如下约束优化问题：

minF（X）=（x₁-5）²+4（x₂-6）²；g₁=64-x₁²-x₂²≤0；g₃=x₁-10≤0的最优解。

解：

1）选择复合形的顶点数k（n+1≤k≤2n），在可行域内构成具有k个顶点的初始复合形。

2）计算复合形各个顶点的目标函数值，比较其大小，找出最好点X^（L）、最坏点X^（H）、及次坏点X^（SH）。计算除去最坏点X^（H）以外的（k-1）个顶点的中心X₀。判别X₀是否可行，若X₀为可行点，则转步骤4）；若X₀为非可行点，则重新确定设计变量的下限和上限值，即令a=X^（L），b=X₀，然后转步骤1），重新构造初始复合形。

3）按式X^（R）=X₀+α（X₀-X^（H））计算映射点X^（R），必要时改变映射系数α的值，直至映射成功，即满足式g_j（X^（R））≤0，（j=1，2，…，m）；F（X^（R））＜F（X^（H））。然后以X^（R）取代X^（H），构成新的复合形。

4）若收敛条件{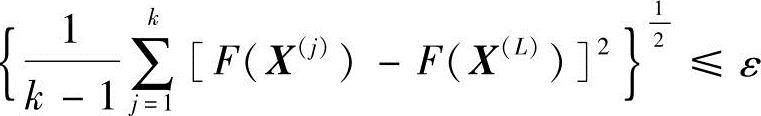得到满足，计算终止。约束最优(www.xing528.com)

解为X^*=X^（L），F（X^*）=F（X^（L））。

复合形方法及源程序//输入值选择n=2，k=3，本程序可以处理n为2或3，k为3或4的情况

4）若收敛条件{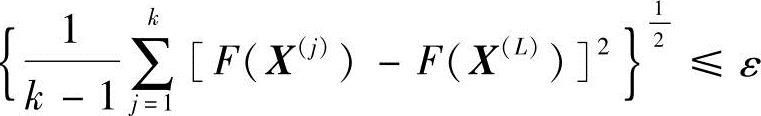得到满足，计算终止。约束最优

解为X^*=X^（L），F（X^*）=F（X^（L））。

复合形方法及源程序//输入值选择n=2，k=3，本程序可以处理n为2或3，k为3或4的情况