构建初始复合形的随机方法：确定可行点作为顶点

构成初始复合形，实际上就是要确定k个可行点作为复合形的顶点。顶点的数目一般取在n+1＜k≤2n范围内。对于维数较低的优化问题，因顶点数目较少，可以由设计者自行试凑出少量的可行点作为复合形的顶点。但对于维数较高的优化问题，这种做法是有困难的，为此提出下面构成初始复合形的一种随机方法。这种方法是先产生k个随机点，然后再把那些非可行随机点逐一调入可行域内，最终使k个随机点都成为可行点而构成初始复合形。具体过程为：

（1）产生k个随机点 利用算法语言的随机数产生函数或计算机中随机数产生子程序，可以在（0，1）开区间内产生均匀分布的随机数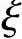_i。利用这个随机数又可按下式产生设计变量分量x_i在给定界限a_i＜x_i＜b_i内的随机数

x_i=a_i+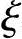_i（b_i-a_i）i=1，2，…，n

利用这n个x_i作为坐标的点X就是一个随机点，其中，第一个点记作X^（1）。

同理，产生n个在（0，1）开区间内的随机数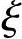i又可获得另一个在开区间a_i，b_i内的随机点X（2）。如此即可连续获得k个随机点X^（1），X^（2），X^（3），…，X^（k）。

因每产生一个随机点，需要n个随机数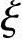i，因此，产生k个随机点总共需要连续发生kn个随机数。

（2）将非可行点调入可行域 用上述方法产生的k个随机点，并不一定都是可行点。但是，只要它们中间至少有一个点在可行域内，就可以用一定的方法将非可行点逐一调入可行域。如果在个别情况下，k个随机点中没有一个是可行点，则应重新产生这些随机点，直到其中至少有一个是可行点为止。

在一般情况下，设已知q个随机点X^（1），X^（2），X^（3），…，X^（q）均为可行点，而X^（q+1）为非可行点。将X^（q+1）调入可行域的步骤：(www.xing528.com)

1）计算q个可行点的点集中心X^（s）。

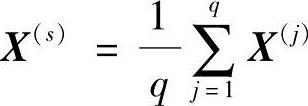
2）将q+1个点向着X（s）点的方向移动，产生新的X^（q+1）点。

X^（q+1）=X^（s）+0.5（X^（q+1）-X^（s））

这个新的X^（q+1）点实际上就是X^（s）与原X^（q+1）两点连线的中点。若新的X^（q+1）点仍为非可行点，则按上式再产生一个新的X^（q+1）点（图7-8），即通过两次迭代而产生新的X^（q+1）点，使它更向X^（s）靠拢，最终使X^（q+1）成为可行点。

按照这种方法，可以继续解决X^（q+2），…，X^（k）的顶点可行性问题。直至全部k个顶点都成为可行点，就构成了在可行域内的初始复合形。