计算步骤和程序框图详解

随机搜索法的计算步骤如下：

1）选择初始点X^（0），检验其是否满足可行性条件。若满足则进行下一步；否则，重新选择初始点。

2）用随机数产生随机方向S，按给定的初始步长α=α₀，沿S方向取得试验点：

X=X^（0）+αS

若X不可行或F（X）＞F（X^（0）），则重新产生新的随机方向并按上式取得新的试验点，直到X可行且F（X）＜F（X^（0）），则继续沿该方向搜索，直至目标函数值不再下降或违背约束条件为止，即完成了一次迭代，将本次搜索的最好可行点作为下次搜索的起点。

3）若每次迭代开始时，在所有随机方向上都找不到一个可行的目标函数值下降点，说明步长较大可能超出可行域，或在可行域内的试探点其函数值不下降，此时可将步长减半后，继续试探，直到步长很小α≤ε（ε为预定精度）且沿所有m个随机方向试探均告失败时，则最后一个最好可行点即为达到预定精度时的约束最优点，迭代结束。随机方向数m不宜太小，一般取m≥50。

以上过程可以用图7-6的程序框图表示。随机搜索法程序编制比较简单，对于那些形态不好的目标函数或可行域有狭长弯道的问题，当搜索方向总数m值较大时，可以提高求解的成功率，一般不会出现伪最优点输出，随机搜索法是一种适用于设计变量较少、成功率较高的优化方法。

例7-1 用随机搜索法求如下二维优化问题：

设计变量：X=（x₀x₁）^T

目标函数：minF（X）=min{（x₀-8）²+（x₁-8）²}

约束条件：(www.xing528.com)

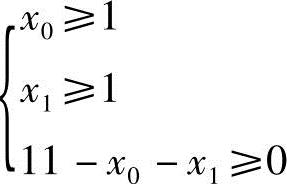
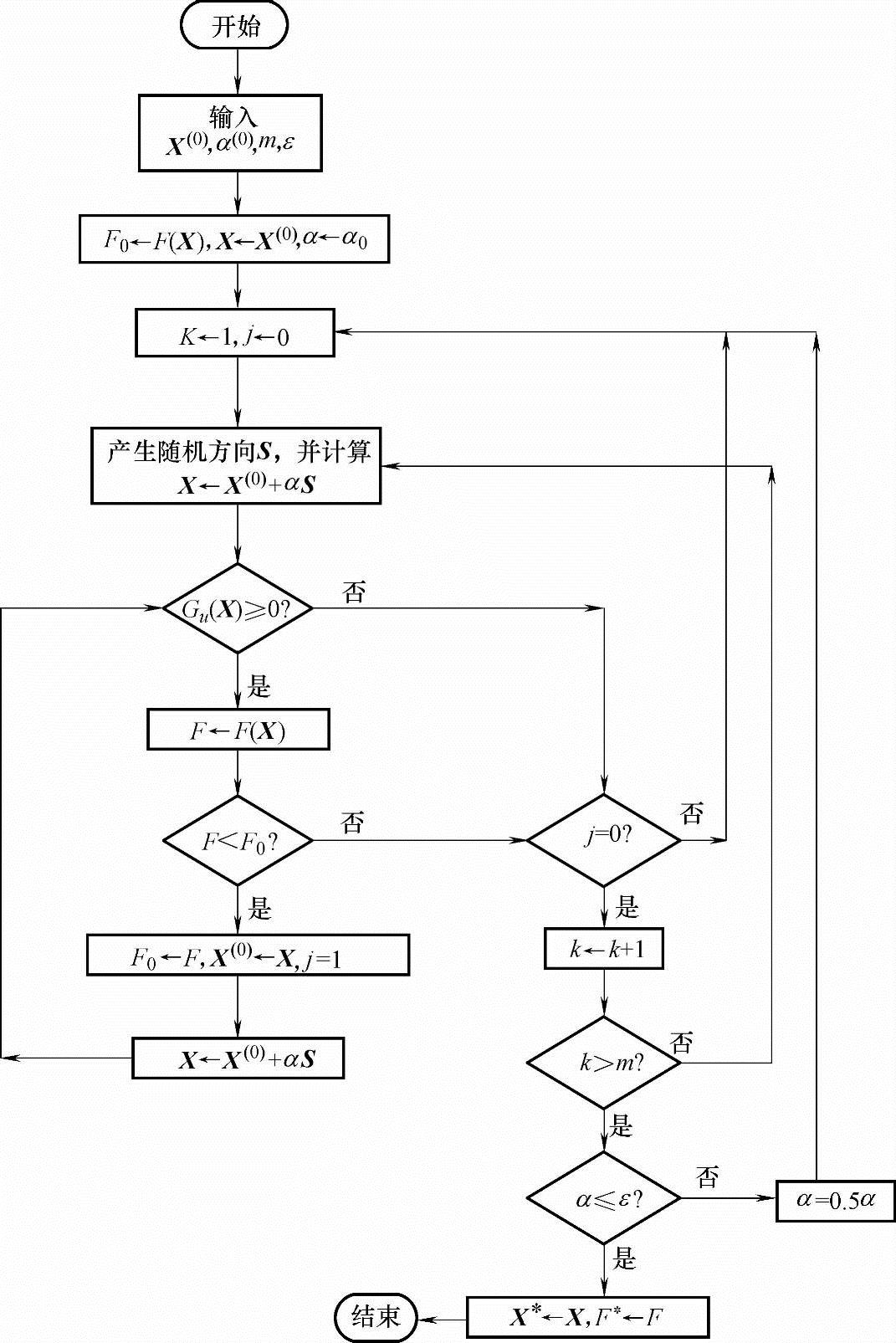
图7-6 随机搜索法的程序框图

解：利用计算机编写程序进行计算。其程序与计算过程如下：

/*随机搜索法*/