数值迭代法：优化目标函数的有效方法

优化问题实质上是求极值的数学问题。这一问题的求优过程有两种求解方法。一种是解析法，即应用数学中的微分学求极值的方法。如果目标函数值在定义区间内连续且存在一阶、二阶偏导数，则目标函数F（X）对各变量的偏导数在该点等于零时，其目标函数在该点有最小函数值，该点即最优点。但是工程中的优化设计，其目标函数和约束函数往往是高次多元函数，求导也存在一定困难，用解析法求解会显得非常复杂。在这种情况下，就只能采用优化问题的另一种解法，即数值迭代法，根据目标函数值的变化规律，沿着能使目标函数值下降的方向，逐步向目标函数值最小点进行搜索。这种方法是一种近似求解函数最小值的计算方法。

1.数值迭代计算的基本概念

数值迭代法的基本思想是：从某已知初始点开始，按照一定的原则和逻辑结构进行目标函数的反复计算，一步步寻求目标函数值不断下降的设计点，直至获得满足给定精度的近似优化解。具有这种特点的计算方法称为数值迭代法。显然，数值迭代的工作量很大，必须借助于计算机编程运算。

现结合二维问题的图形（图7-3）来说明优化算法的迭代过程。设优化点为X^*，先从某一个选定的初始点X^（0）（图7-3画出了从两个不同的初始点X₁^（0）和X₂^（0）开始所经过的迭代过程）开始，沿某优化方法所规定的方向S^（0），确定适当的初始步长α^（0）。从初始点开始，按下式产生一个新的设计点X^（1）：

X^（1）=X^（0）+α^（0）S^（0）

使满足

F（X^（1））＜F（X^（0）） 且X^（1）∈D

则X^（1）就是一个优于X（0）的设计点。

然后以X^（1）为新起点，按类似方法产生下一个新设

计点X^（2）。如此反复迭代计算，第k+1次迭代为

X^（k+1）=X^（k）+α^（k）S^（k） （7-9）

式中，X（k+1），X（k）分别为k+1，k次的迭代点；S（k）为第k次迭代计算的优化方向；α（k）为第k次迭代计算的步长。

使满足

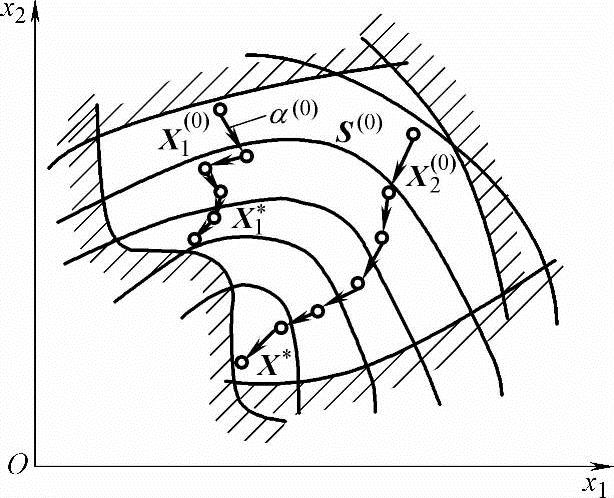
图7-3 优化算法的迭代过程(www.xing528.com)

F（X^（k+1））＜F（X^（k）） 且X^（k+1）∈D （7-10）

由于每次迭代，其目标函数值均有所下降，故最后必逼近最优点X^*。式（7-9）即为基本迭代公式。

按式（7-9）进行一系列迭代计算的基本思想为“下山法”，即每迭代一步都应该使目标函数值有所下降，同时还要为下一步移动的方向提供有用的信息。由以上迭代方程可以看出，优化方法的主要问题是解决如何确定迭代方向S^（k）和迭代步长α^（k）的问题，以使得每次迭代其目标函数值稳定下降。

2.迭代计算的终止准则

从理论上说，任何一种迭代计算法都可以无穷的序列{X^（k），k=0，1…}无限制地进行下去，而且当k→∞时，应该有X^（k）→X^*。但实际上，优化计算不可能也不必要按上述迭代过程无限制地进行下去，因此有必要有一迭代终止的准则，只要达到预先给定的精度便可以终止迭代计算，并认为已求得近似的最优解。从理论上讲，希望迭代最终优化点与理论极小点之间的距离足够小时，终止迭代。但实际上上述要求无法办到，因为优化设计前理论极小点是未知的，而只能从这一迭代序列中提供的信息来建立终止迭代准则。一般常用的迭代终止准则有：

（1）点距准则 前后两次迭代点X^（k+1）、X^（k）之间矢量差的模已充分小，达到预定的精度值ε时，即

则认为X^（k+1）≈X^*，终止迭代。

（2）函数下降量准则 前后两次迭代点的函数值下降量已充分小，达到预定的精度ε时，即

F（X^（k+1））-F（X^（k））≤ε （7-13）

或当F（X^（k+1））≠0时

则认为X（k+1）≈X^*，终止迭代。

以上各式中的ε代表收敛精度值，其值可以根据不同的迭代计算方法和工程实际问题的性质而定。这两种终止准则都在一定程度上反映了达到最优点的程度，但是都各有一定的局限性。单独用某一种终止准则遇到一些特殊形态的目标函数时，可能会造成迭代过早结束，因此最好同时用这两种终止准则，以保证能收敛于最优点。式（7-14）比式（7-13）更能反映目标函数的变化程度，但当F（X^（k+1））→0时，终止准则不能采用式（7-14），否则会致使计算提前终止。在优化问题的实际计算中，还常常附加最大迭代次数作为终止准则，以免计算时间过长或死循环。