优化问题在几何描述中的应用介绍

上一节用数学公式表示了优化设计的数学模型。为了有助于建立优化设计的某些概念，增强感性认识，现将有关设计变量、目标函数和约束条件之间的关系以及欲寻求的最优方案等作一几何解释。

求解n维约束优化设计问题的解，可以想象为在n维设计空间的可行域内，找出一个与n+1维目标函数超曲面的最小值相对应的设计点X*。由于n维问题难以用平面图形表示，因而现以一个二维优化问题来作解释。

设有一个二维优化数学模型为

minF（X）=（x₁-2）2+x²₂

s.t.G₁（X）=x₁≥0

G₂（X）=x₂≥0

G₃（X）=x₁-x₂+2≥0

G₄（X）=x₂-x²₁-1≥0

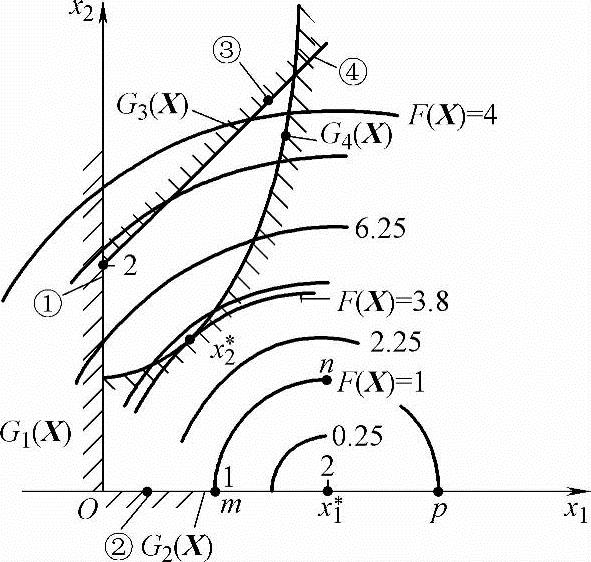
图7-2 优化问题的几何描述(www.xing528.com)

对于这样一个优化问题可用图7-2的几何图形来说明某些概念。

该目标函数可描述为x₁、x₂和F（X）为坐标轴的三维空间的一个二次曲面。该曲面上每一点都有与之对应的目标函数值，凡目标函数值相等的点所连成的曲线投影在设计空间x₁Ox₂内得到的一条曲线，称为目标函数等值线，如图7-2所示。对于上述优化数学模型，目标函数等于c_i时的等值线可以表示为

F（X）=（x₁-2）2+x²₂=ci

该曲线是以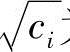为半径，（2，0）为圆心的圆。即在该圆上任意点（x₁，x₂）处其目标函数F（X）值均为c_i。若令c_i为一系列值，对应于一系列不同的目标函数值，就可以得到该目标函数的一系列等值线，称为目标函数的等值线族。对于上述优化数学模型，等值线族是以（2，0）为圆心，以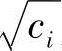为半径的一族同心圆。极值理论证明，一般情况下，等值线为一族近似的椭圆，本例的圆族是椭圆族的一种特例。本例中若无约束时，其函数极小值即无约束最优值F₁^*=0，其最优点为X₁^*=（2 0）^T。

若令四个约束方程为零，在x₁Ox₂空间中可画出四条曲线，在约束曲线的一侧有G_v（X）≥0，另一侧有G_v（X）＜0。由G_v（X）≥0围成的区域称为可行域（如图7-2中阴影所包围部分），记作：

D={X|G_v（X）≥0u=1，2，…，z}

其他部分称为非可行域。设计点必须在可行域内选取，这些设计点称为可行设计点。由图7-2得：满足G₄（X）条件必满足G₂（X）。故第二个约束条件是一种消极约束。但必须指出，当问题复杂时往往不能预先观察出哪些约束为消极约束，因此在数学模型中仍需列出全部约束条件。本例可行域中的约束最优点X^*=（0.58 1.34）^T，其最优值F^*=3.8。该最优点X^*是F（X）=3.8的等值线与约束曲线G₄（X）=0的切点。

因此，对于一个n维的约束优化设计问题，几何描述为：在由n个设计变量所构成的实欧设计空间Rⁿ中，有z个不等式约束的超曲面将其划分成一个可行域D和一个非可行域，当目标函数取一系列数值时，就在可行域内构成一系列表示目标函数变化的等值超曲面。优化问题就是要在D中找到一个设计点X*，使其目标函数值为最小值F^*=F（X^*）。实际上，对于多数约束优化问题来说，这一点多半就是目标函数等值超曲面与约束超曲面的一个切点，而对于无约束优化问题，这一点就是目标函数的极值点。