根据轨迹设计四杆机构

实现已知轨迹的设计问题是指设计一连杆机构，其连杆上某点能再现（或称复演）所要求的轨迹。连杆上任一点的轨迹称为连杆曲线。表6-1给出了不同机构连杆上若干点不同的连杆曲线，可供设计中参考。除用解析法设计机构外，还有一种图谱综合法，即按图谱选择与要求相近的曲线来确定机构的尺寸。这里简单介绍按位移矩阵法进行机构设计的方法。

设给定轨迹的函数为y=f（x），设计一四杆机构并使其连杆上P点的n个位置能拟合给定轨迹，即P点的坐标值满足给定的函数关系

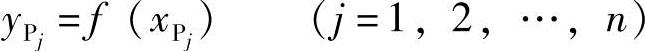
如图6-13所示，P点的位置取决于连杆位置，当P点各位置已知时可以写出连杆位移矩阵。应该注意到该位移矩阵中连杆的相对转角θ_j是未知的，因此无法单独求出某一连架杆的运动副未知坐标值。如果根据定杆长约束条件写出两连架杆的约束方程并联立，则可求出连架杆运动副坐标值及连杆各未知的相对转角θ_j。连杆的位移矩阵为

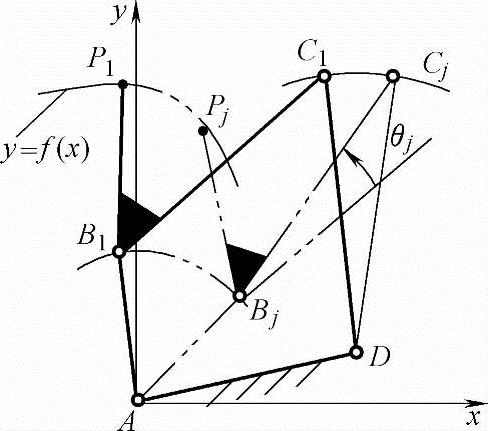
图6-13 轨迹综合 的机构模型

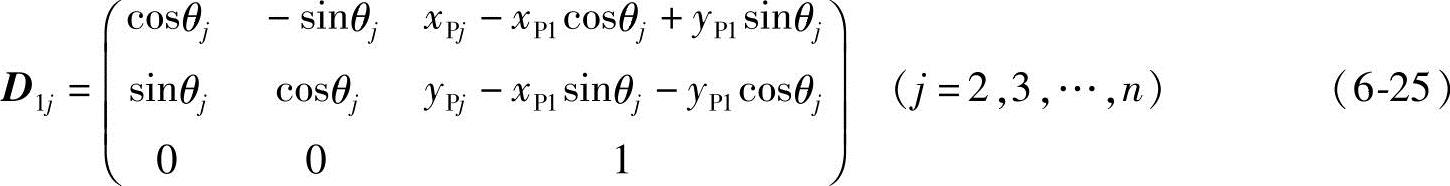
式中，θ_j为未知量。

B_j、C_j与B₁、C₁坐标间的关系可用位移矩阵表示

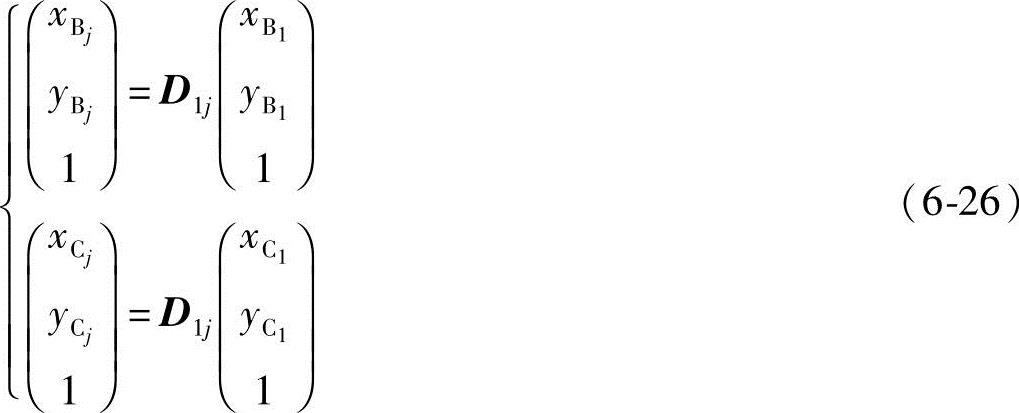
两连架杆杆长约束方程为

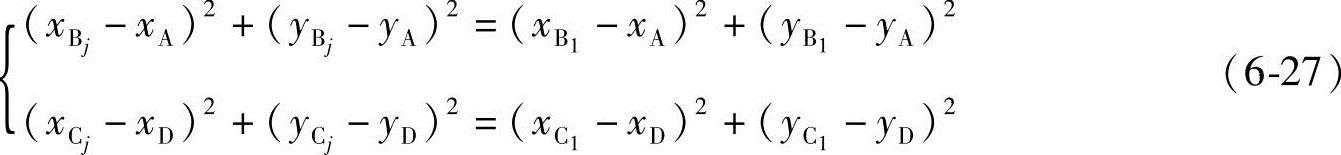
将式（6-25）、式（6-26）代入式（6-27）得

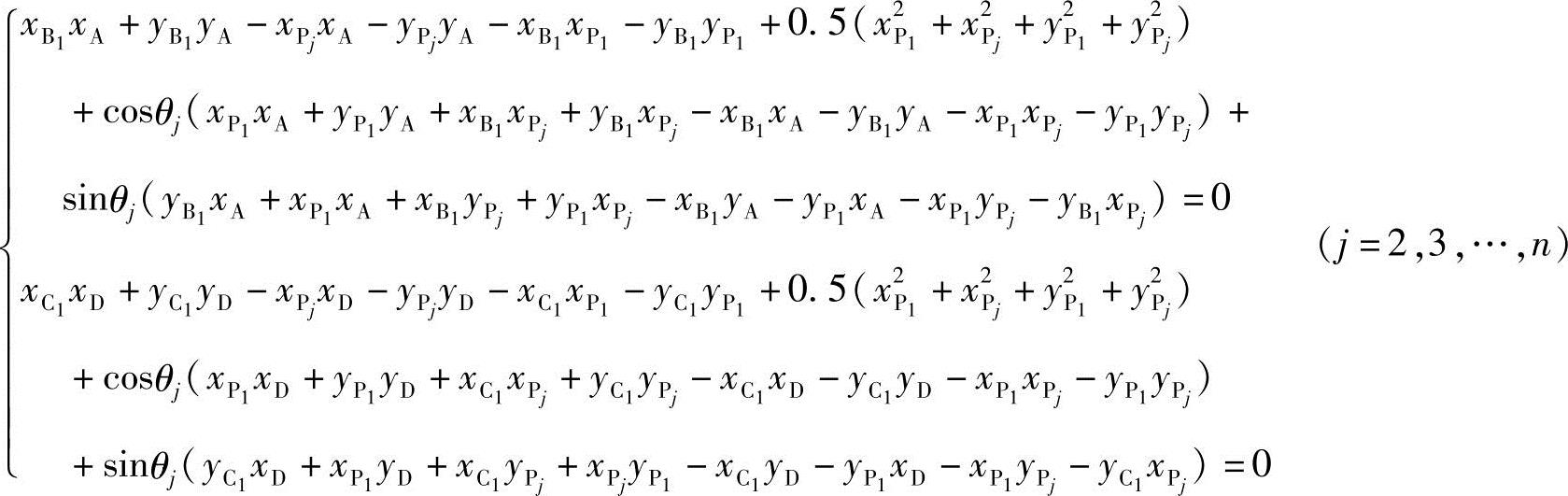
（6-28）(www.xing528.com)

式（6-28）表示各运动副位置1坐标与P点给定坐标值以及连杆相对转角间的关系，已知量为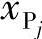、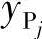（j=1，2，…，n），未知量为x_A、y_A、x_D、y_D、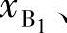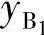、、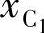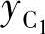以及连杆相对转角θ_j（j=2，3，…，n）。可见若给出n个已知点位置，则方程数为2（n-1），待定参数包括8个运动副坐标及n-1个连杆转角。若已有k个待定参数赋值，则待定参数总计为n+7-k。因此有定解的条件为2（n-1）=n+7-k，即

n=9-k （6-29）

式（6-29）表示有定解的给定点数位n与预先赋值的待定参数数目k间的关系。当k=0时，n=9，即四杆机构最多只能精确实现给定函数轨迹上的9个点。当给定5个轨迹点位时，必须预先给定4个待求量赋值才有定解。当精确实现的点数n=2～9时，其设计方程数目，未知参数数目及预先赋值的待定参数数目见表6-1。

表 6-1

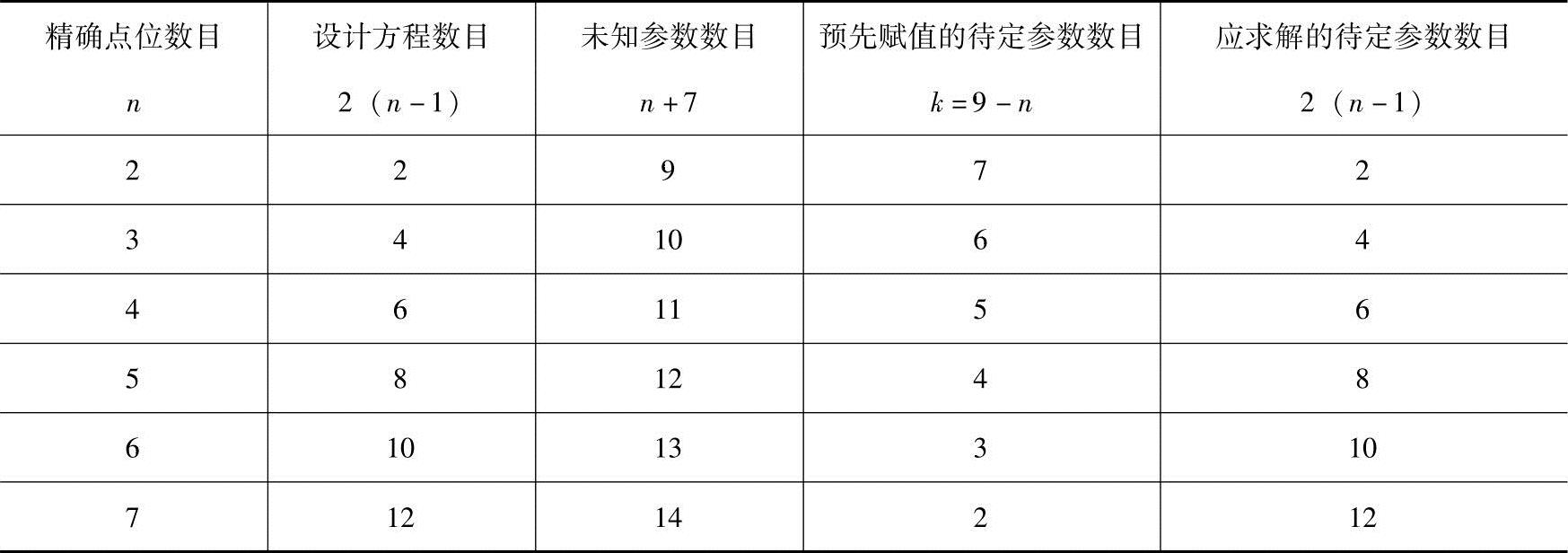
理论上铰链四杆机构能精确实现轨迹上的9个点位，但由于上述设计方程为非线性方程组，只能借助于计算机进行数值迭代求解其逼近值。另外，当点位超过6个时，其是否有解在很大程度上取决于迭代计算所取初值、要求的计算精度及所选点在轨迹上的位置，有时求

解会十分困难。在设计中如果选值不当，还可能出现轨迹失调，即机构运动顺序与轨迹顺序不协调的现象。

例6-7 已知轨迹上5个点位的坐标值P₁（1，1），P₂（2，0.5），P₃（3，1.5），P₄（2，2），P₅（1.5，1.9）。试设计复演5个点位的铰链四杆机构。

解：如表6-1所示，当n=5时可列出8个方程，未知参数数目为12，若有定解必须预先对4个待求量赋值。设x_A=2.1，y_A=0.6；x_D=1.5，y_D=4.2。

将5个点位的P点坐标值代入式（6-28）得8个非线性方程。用牛顿-拉普森（Newton-Raphson）法求解，其结果为

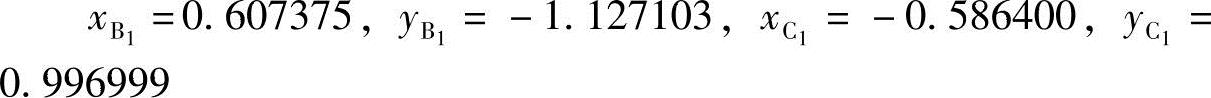
设计所得机构如图6-14所示。

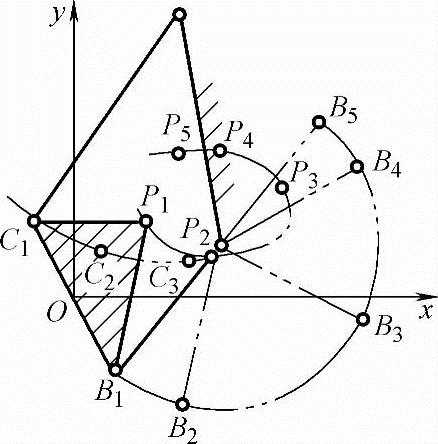
图6-14 四杆机构复演