如图6-9所示,若两连架杆初始角为φ0、ψ0,相对初始角的转角分别为φj、ψj。两连架杆对应位置以ψ=ψ(φ)表示。在按ψ=ψ(φ)设计铰链四杆机构的问题中,由于φj、ψj只与机构的相对尺寸有关,所以设机架AD沿x正向并令AD=1。此时A、D支座位置已知:A=(0 0)T,D=(1 0)T。因此,该机构综合问题即为确定运动副B、C的坐标值。
由于连杆BC的位置未知,故不能写出连杆的位移矩阵。而机构位置的综合问题实际上即为机构形状的综合问题。因此可将机构在第j位置的形状ABjCjD刚化,采用变换机架的方法(即以DC1为机架)将刚体ABjCjD绕D反转ψj角使DCj与DC1重合,机构从AB1C1D到位置ABjCjD的综合问题可以转化为假想以DC1为机架,机构从位置DAB1C1到位置DAj′Bj′C1的综合问题,此时AB为连杆,这样就可以应用连杆位移矩阵求解。
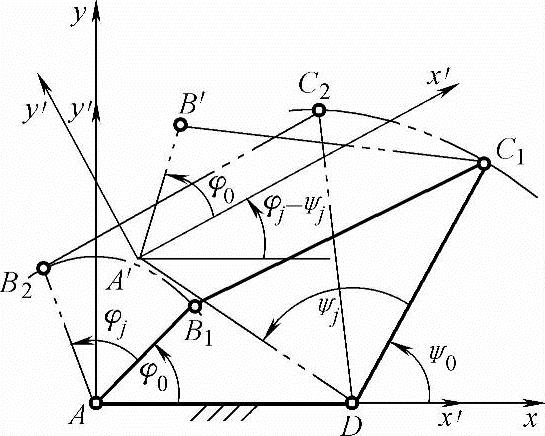
图6-9 机构的机架变换
现分析以AB为假想连杆,从位置AB1到Aj′Bj′时如何写出其位移矩阵。构件从AB1到Aj′Bj′可以看成AB1首先绕A转动φj角到达ABj,再使ABj绕D转动-ψj角到达Aj′Bj′,可见此时与AB1固定的动坐标系Ax′y′转动φj-ψj后到达Aj′x′y′。动坐标原点Aj′的位移d13、d23分别为
d13=1-cosψjd23=sinψj
故Aj′Bj′在定坐标系中相对于DC1的位移矩阵有如下形式
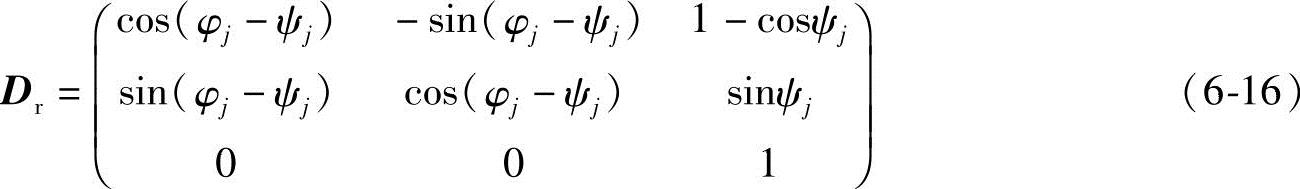
机构综合即确定运动副B1、C1的位置,根据BC杆长不变列出约束方程:
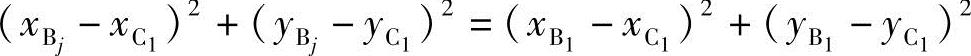
式中,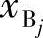 、
、 可用相对位移矩阵Dr以
可用相对位移矩阵Dr以 、
、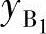 表示:
表示:
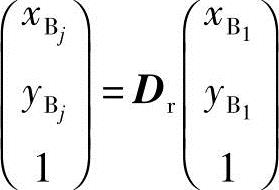
将上式代入约束方程经整理后可得到与式(6-10)、式(6-11)相同的形式。应注意在相对运动中,B1为可动运动副,C1为固定支座。因此得到
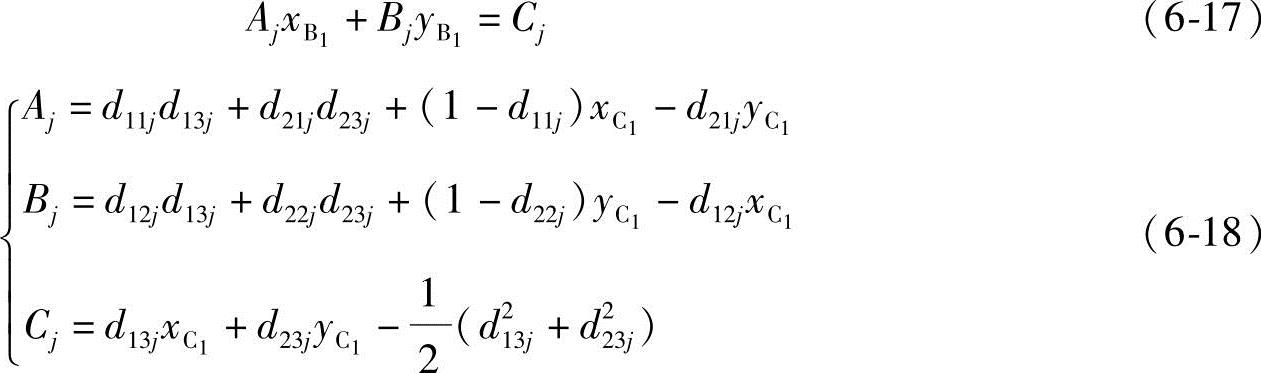
其中d11j=cos(φj-ψj),d12j=-sin(φj-ψj),d13j=1-cosψj,d21j=sin(φj-ψj),d22j=cos(φj-ψj),d23j=sinψj (j=2,3,…,n)。
给定n个位置可以写出n-1个方程,待求量为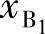 、
、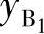 、
、 、
、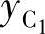 ,所以当两连架杆对应位置数n=5时有定解。当n=3时,必须先给定两个待求量的值才有定解。
,所以当两连架杆对应位置数n=5时有定解。当n=3时,必须先给定两个待求量的值才有定解。
例6-5 如图6-10所示,给定两连架杆对应角位移:φ2=-30°,ψ2=-20°,φ3=-60°,ψ3=-40°及两初始坐标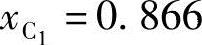 ,
,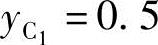 。试设计四杆机构。(https://www.xing528.com)
。试设计四杆机构。(https://www.xing528.com)

图6-10 设计四杆机构
解:写出相对位移矩阵[Dr1j](j=2,3)
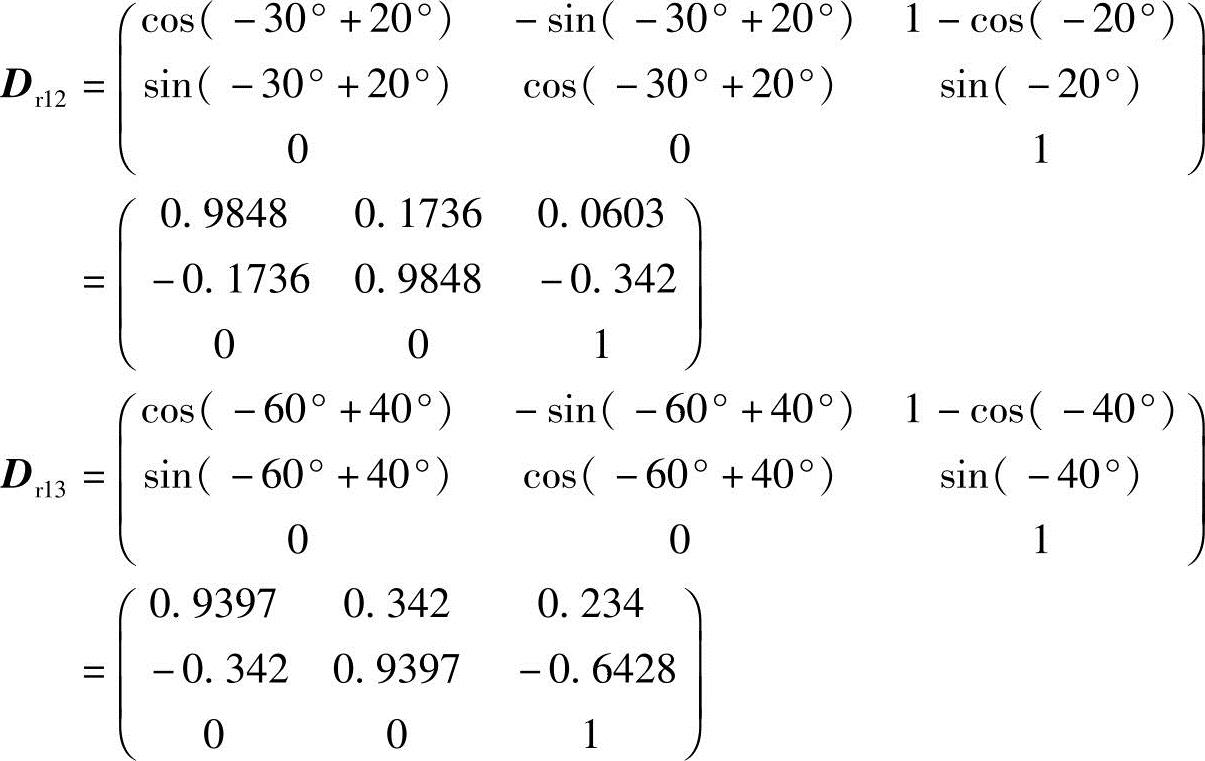
将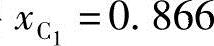 ,
,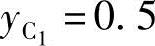 代入式(6-18)中求出Aj、Bj、Cj(j=2,3):
代入式(6-18)中求出Aj、Bj、Cj(j=2,3):
A2=0.9848×0.0603+(-0.1736)×(-0.342)+(1-0.9848)×0.866+0.1736×0.5=0.21872
B2=0.1736×0.0603+0.9848×(-0.342)+(1-0.9848)×0.5-0.1736×0.866=-0.4691
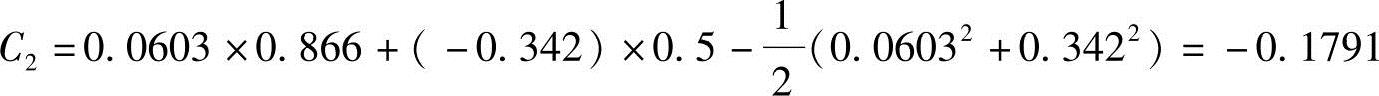
A3=0.9397×0.234+(-0.342)×(-0.6428)+(1-0.9397)×0.866+0.342×0.5=0.66295
B3=0.342×0.234-0.9397×0.6428+(1-0.9397)×0.5-0.342×0.866=-0.7900
C3=0.234×0.866+(-0.6428)×0.5-0.5(0.2342+0.64282)=-0.35273
再由式(6-17)列出线性方程组:

解得 ,
,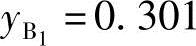 。
。
各杆长为
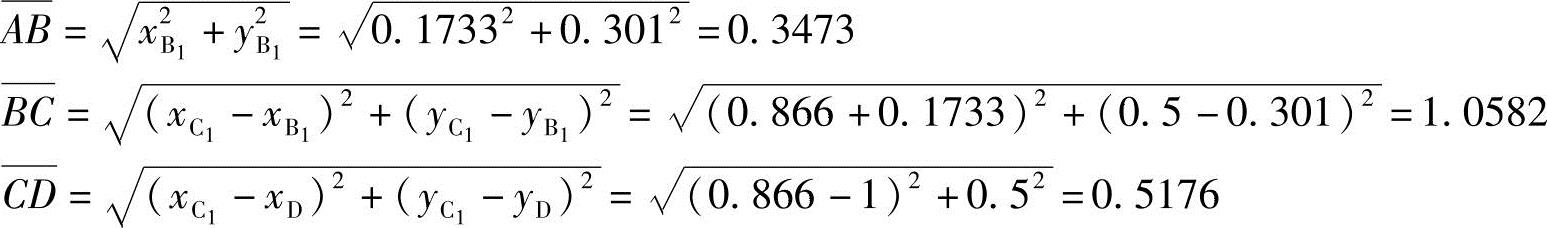
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




