按连杆位置设计曲柄滑块机构

按给定的连杆位置综合曲柄滑块机构时，与铰链四杆机构的综合方法一样（图6-6），可取位置1为参考位置写出连杆的位移矩阵。先根据杆长不变约束条件求A、B坐标值，再按定斜率约束方程求解滑块铰链T的位置。

现讨论滑块铰链T的约束直线方程，设已知连杆的三个位置，则滑块铰链T的约束方程为

或写成行列式形式

图6-6 曲柄滑块机构的综合模型

将以上行列式展开

式中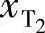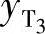，、、、均可用位移矩阵以、代替。

式中，d_ikj（i=1，2，3；k=1，2，3；j=1，2，3）均为已知，求出、与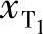、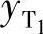的关系后代入式（6-13）可解出、。

滑块的导路倾斜角α₄为

tanα₄=（y_T2-y_T1）/（x_T2-x_T1） （6-15）

由于三个位置才能列出一个定斜率方程，故当已知n位置时可列n-2个方程。可见方程数与待求量（x_T1，y_T1）相等时，即n=4时有定解。上述n=3的情况只能求一个未知量，

因此、之一先给定时有定解。

例6-4 已知连杆三位置，P₁=（1 1）^T，P₂=（2 0.5）^T，P₃=（3 1.5）^T；θ₂=0，θ₃=45°。设固定支座A=（5 0）T，滑块铰链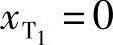，试设计该曲柄滑块机构。

解：列出两个有限位移矩阵

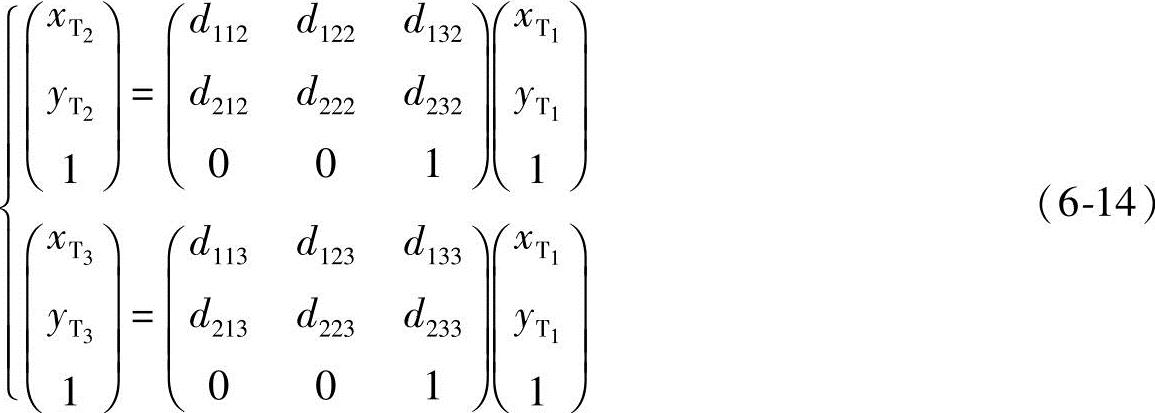
(https://www.xing528.com)

先求铰链B的坐标x_B1、y_B1，因固定支座A=（5 0）^T。由式（6-11）得A₂=1，B₂=-0.5，C₂=4.375，A₃=3.6467，B₃=1.47465，C₃=10.4963。将系数值代入式（6-10），

则有

解得，。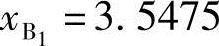

再求滑块铰链T的坐标、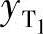。将位移矩阵代入式（6-14），得

将以上结果代入式（6-13），得

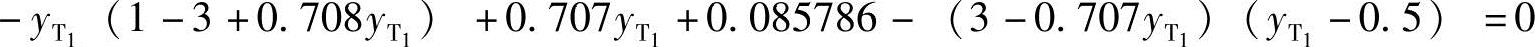
解得。

由式（6-15）解得导路倾角

根据几何关系解得机构各杆长

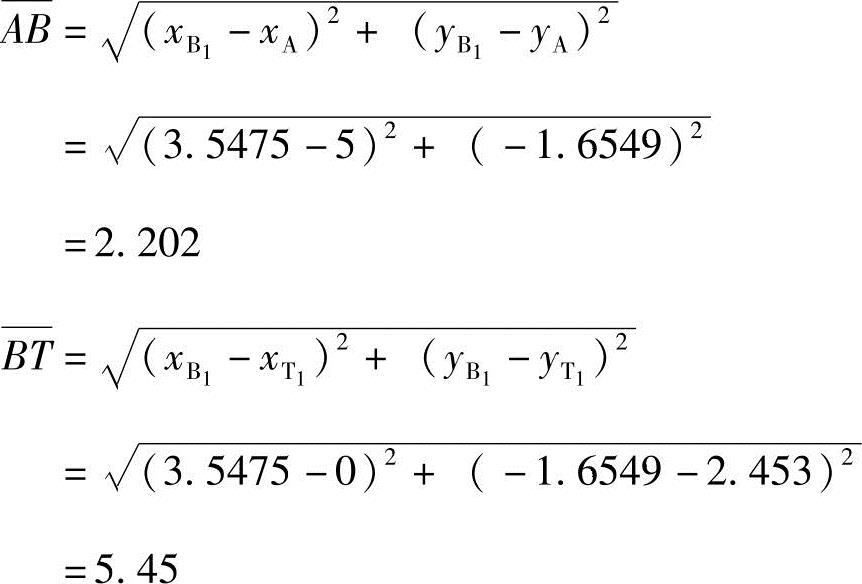
设计所得机构如图6-7所示。

图6-7 曲柄滑块机构综合结果