设计铰链四杆机构的连杆位置优化

如图6-5所示，给定连杆BC的各位置θ_j。θ_j为连杆标线与其第一位置的相对转角（逆时针为正）。要求设计四杆机构实现给定的连杆各位置，即确定支座A、D和第一位置时运动副B₁、C₁的坐标。

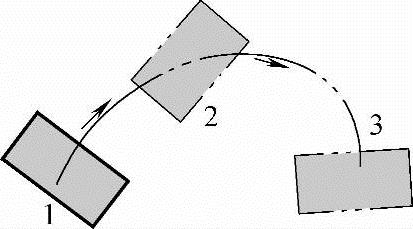
图6-4 刚体导引

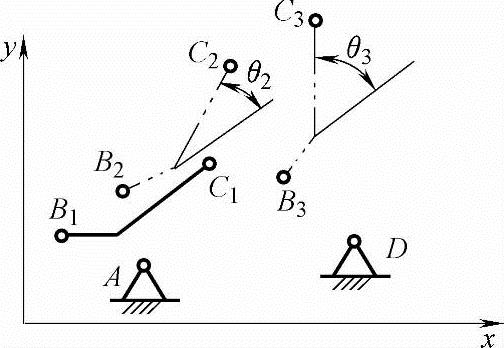
图6-5 刚体导引机构模型

设可动运动副坐标以（x_j，y_j）表示，支座运动副坐标以（x₀，y₀）表示。根据可动运动副与其转动支座间距离不变（即杆长不变），可列出如下方程：

（x_j-x₀）²+（y_j-y₀）²=（x₁-x₀）²+（y₁-y₀）² （6-8）

根据位移矩阵可写出（x_j，y_j）与（x₁，y₁）间的位移方程为

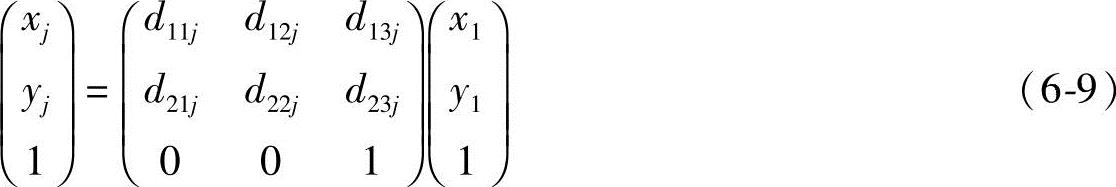
将式（6-9）代入式（6-8）可消去x_j、y_j，简化后得

A_jx₁+B_jy₁=C_j （6-10）

其中

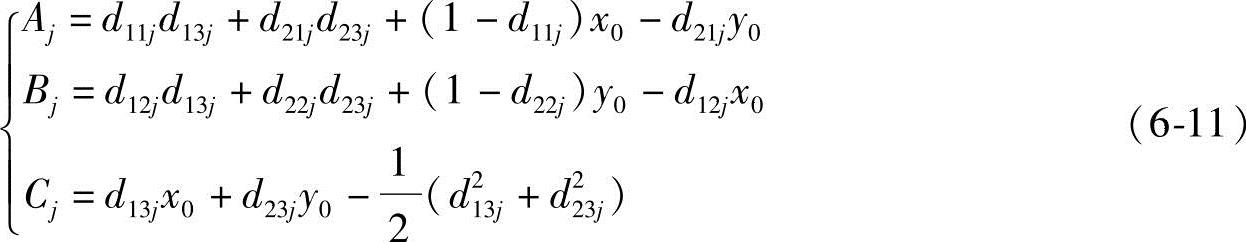
由式（6-10）和式（6-11）知，未知量为x₁、y₁、x₀、y₀，由于连杆的n个位置可列出n-1个方程，只有方程数与未知量相等时（n-1=4），有定解，故当给定连杆五位置时式（6-10）、式（6-11）有定解。若已知连杆三位置，仅可列出两个方程，四个未知量中必须预先给定两个才有定解。一般给定支座位置（x₀，y₀），此时式（6-11）中的A_j、B_j、C_j为常数，故式（6-10）为j=2、3的线性方程组。

将运动副B₁和支座A的坐标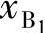、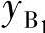和x_A、y_A分别置换式（6-10）、式（6-11）中的x₁、y₁和x₀、y₀，可求出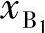、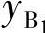和x_A、y_A。同理可求出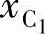、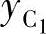和x_D、y_D。

例6-3 已知连杆三位置P₁=（0 1）^T，P₂=（1.6 2.2）^T，P₃=（3.4 1.9）^T；θ₂=0，θ₃=30°。并给定支座位置A=（0 0）^T，D=（5 0）^T。试设计一铰链四杆机构。

解：将给定参考点P₁、P₂、P₃的坐标及转角代入式（6-4）：

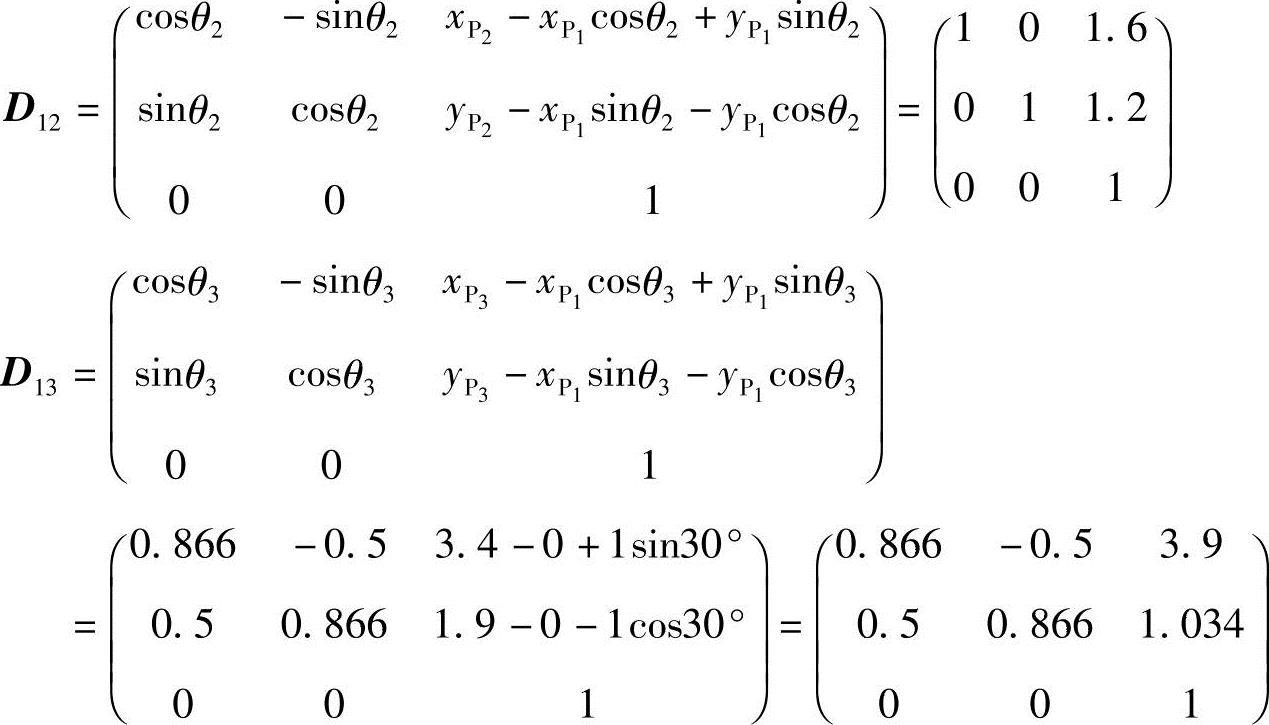
先计算支座A及运动副B₁的坐标值。由于A=（0 0）^T，由式（6-11）得(www.xing528.com)

A₂=1×1.6+0×1.2+（1-1）x_A-0y_A=1.6

B₂=0×1.6+1×1.2+（1-1）y_A-0x_A=1.2

C₂=1.6×0+1.2×0-0.5（1.6²+1.2²）=-2

同理得A₃=3.8944，B₃=-1.0546，C₃=-8.1396

将A_j、B_j和C_j（j=2，3）代入式（6-10）有

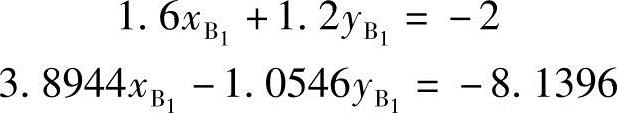
解出，。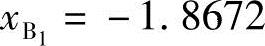

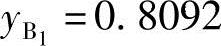再计算支座D及运动副C₁的坐标值，由于D=（5 0）^T，根据D₁₂，D₁₃及式（6-11）

得

A₂=1×1.6+0×1.2+（1-1）x_D-0×y_D=1.6

B₂=0×1.6+1×1.2+（1-1）y_D-0×x_D=1.2

C₂=1.6×x_D+1.2×y_D-0.5（1.6²+1.2²）=6

同理得A₃=4.5644，B₃=1.4454，C₃=11.36042

将A_j、B_j、Cj（j=2，3）代入式（6-10）得线性方程组：

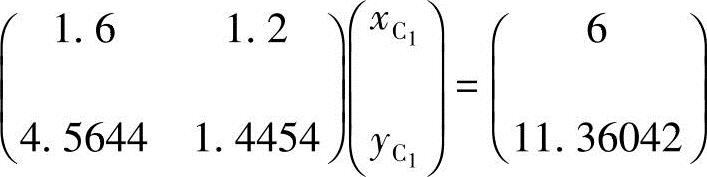
解得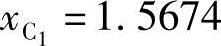，y。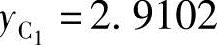

当求出该机构位置1时连杆铰链点B₁、C₁的坐标后，即可根据两点间的距离公式求出各杆长度。