刚体平面有限位移矩阵的应用与分析

如图6-1所示，要求沙箱运动占有三个位置1、2、3。其上P点三位置的坐标值及其姿态均已知，希望点P绕固定支座O_Q转动占据给定三位置，但P点的转动中心却在点O_P。为了在沙箱上根据已知点P_j（j=1，2，3）找到另外一点Q_j（j=1，2，3），使其转动中心位于固定支座O_Q。需要建立平面运动刚体上未知点与已知点间的坐标方程式。

如图6-2所示，刚体的位置可用其上一直线PQ表示。其任意位置j用P_jQ_j（j=1，2，3）表示。

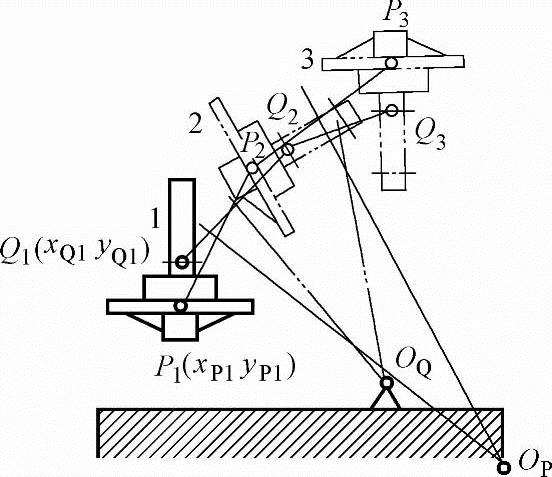
图6-1 沙箱的运动

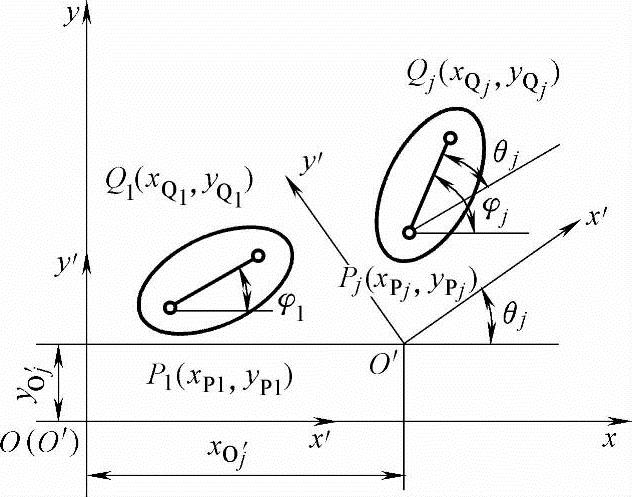
图6-2 刚体的有限位移图

Oxy为固定坐标系，与刚体PQ固定的O′x′y′为动坐标系。位置P₁Q₁处动、定坐标系重合。现使刚体与动坐标系O′x′y′一起相对于定坐标系Oxy作有限位移，到任意位置j。动坐标系相对定坐标系的转角（即刚体P_jQ_j相对P₁Q₁的转角）用θ_j表示。

θ_j=φ_j-φ₁ （6-1）

若已知P点的位置参数，该刚体上另一点Q与已知点P间的关系式为

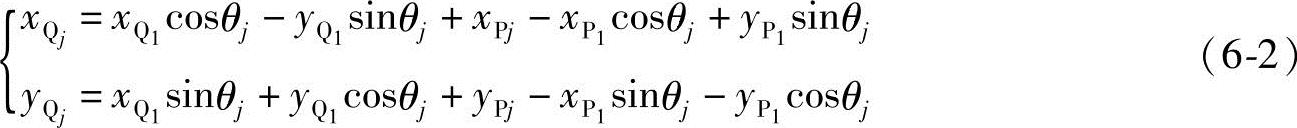
式（6-2）可写成矩阵表达式：

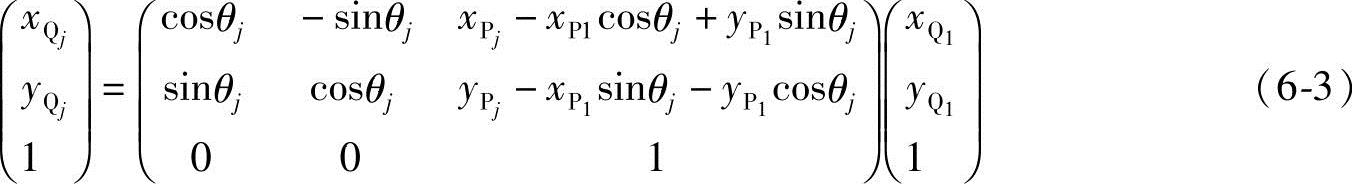
若

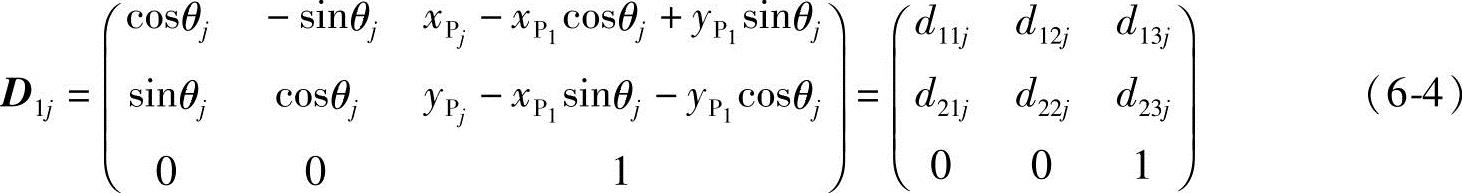
式中，d_13j=x_Pj-x_P1cosθ_j+y_P1sinθ_j；d_23j=y_Pj-x_P1sinθ_j-y_P1cosθ_j，即动坐标系的原点O′在定坐标系中的坐标值x_O′_j、y_O′_j，故D_1j称为从位置1到位置j的刚体平面运动的位移矩阵。因此，只要已知刚体的n个位置（即刚体某点的n个坐标值及其n-1个平面运动转角）就可以写出n-1个位移矩阵。

则式（6-3）可表达为

设刚体绕z轴转动，即动坐标系原点位置不变而绕定坐标系原点转动。此时d₁₃=d₂₃=0，其位移矩阵用R_1j表示，称为平面转动矩阵。有如下形式

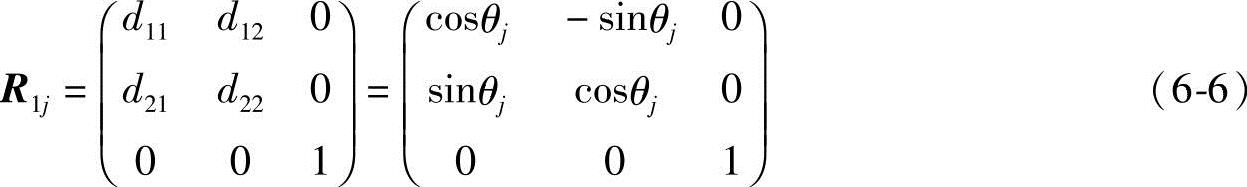(www.xing528.com)

当刚体作平动，即θ_j=0时，cosθ_j=1，sinθ_j=0。位移矩阵用T_1j表示，称为平动矩阵，并有如下形式

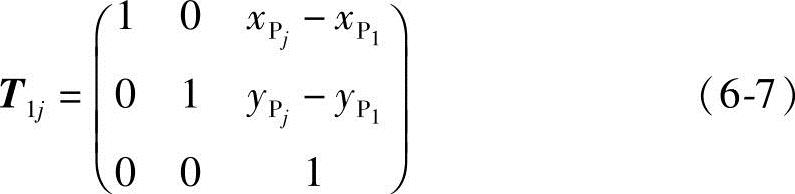
例6-1 如图6-3所示，构件PQ作平面有限位移，已知构件初位置P₁=（1 1）^T，Q₁=（3 1）^T，若P点到位置P₂=（3 2）^T并相对第一位置转角为θ₂=60°，求Q₂。

解：写出位移矩阵式并代入已知数值。

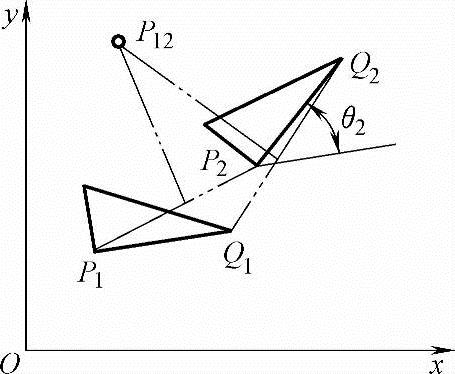
图6-3 刚体位移

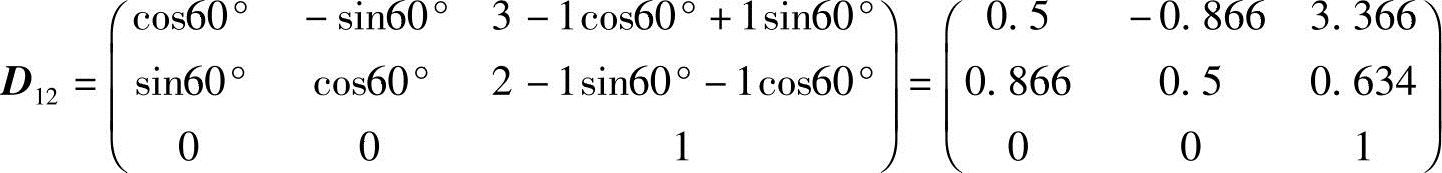
将上式代入式（6-3），得

解得Q₂=（4.000 3.732）^T。

例6-2 如图6-3所示，已知条件同例6-1，求构件从位置P₁Q₁到P₂Q₂的转动中心P₁₂。

解：由于P₁₂为转动中心，故从位置1到位置2时P₁₂点不动，即运动前后P₁₂的坐标值不变。将位移矩阵代入式（6-3），得

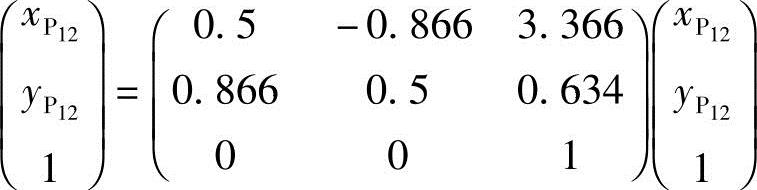
展开后

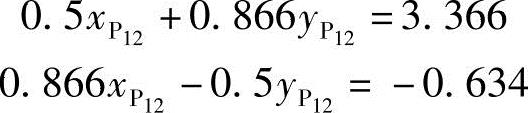
解得