飞剪机构型综合：避免制动瓦不均现象的设计优化

如图5-23所示，飞剪机构一般应用于轧钢厂的轧制生产线上，用来将在辊道上以已知速度运行的钢材剪切成给定长度的成品。由于飞剪机完成周期性间歇冲击作业，因此，其剪切机构一般不选用高副机构。

（1）生产工艺对飞剪机构的要求 收集有关资料得到：

给定长度：L=1m。

钢板厚度：Δb=1～2mm。

剪切力：F=10t=98kN。

支座A距辊道面高度：H≥250mm。

钢材运行速度：υ_t=2m/s。

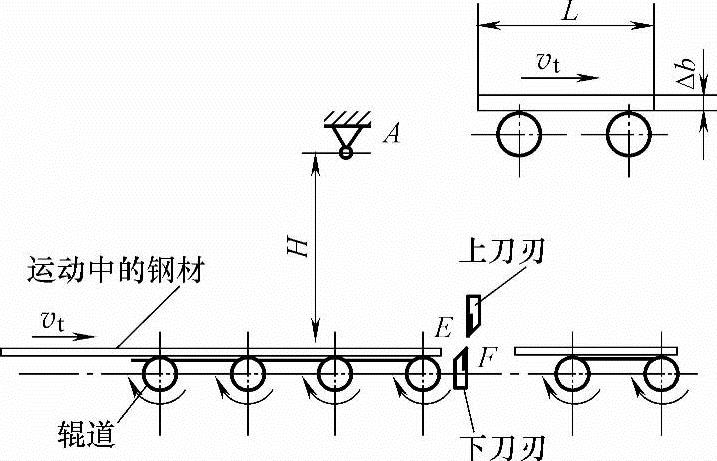
图5-23 对飞剪机构的工艺要求

（2）把生产工艺的要求转化为对机构的动作要求 对飞剪机构剪切动作的要求：

1）为完成剪切，上下刀刃应完成相对分合运动。

2）为剪切运动中的钢材，上下刀刃在完成相对分合运动的同时还应有沿钢材方向的运动。

3）根据以上要求可知，上下刀刃运动轨迹之一应为封闭曲线，如图5-24a、b、c所示。图5-24d上下刀刃轨迹均为非封闭曲线，使得飞剪机构在空行程中沿钢材运动方向逆向剪切，这是不允许的。

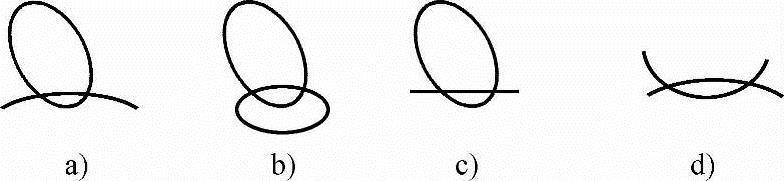
图5-24 剪切动作要求

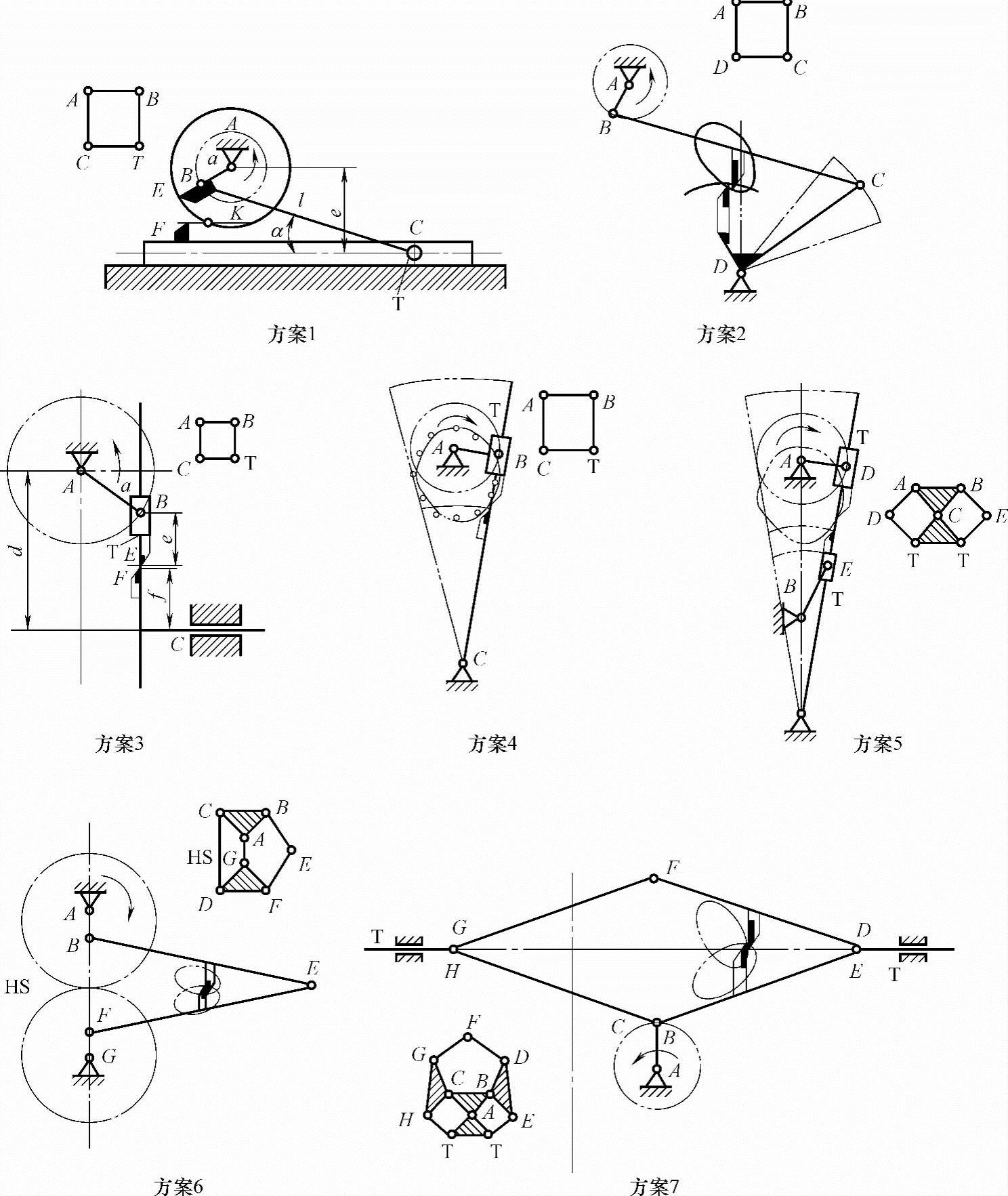
图5-25 飞剪机构方案图

剪切时对运动参数的要求：

1）曲柄转一圈对钢材剪切一次。计算出曲柄角速度：ω₁=2πυ_t/L=2π×2/1=4π/s。

2）剪切时，上下刀刃应与钢材运动同步。若剪切时刀刃沿钢材方向的速度过小，从轧机送出的钢材将会堆积。故一般希望刀刃速度略大于钢材运动速度，即

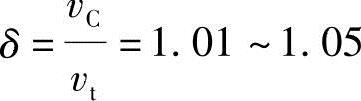
υ_C=（υ_Et+υ_Ft）/2

式中，υ_Et、υF_t分别为上、下刀刃的水平速度；δ为拉钢系数；υ_C为刀刃水平平均速度。

3）上下刀刃运动速度相同。剪切时，若上刀刃大于下刀刃速度，则钢材出现斜面断口；

若上刀刃小于下刀刃速度，有可能产生碰刀。故上下刀刃相对误差要小于其许用值：

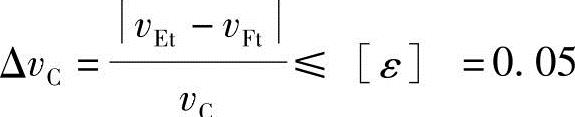
4）最好能对钢材的剪切长度L进行调节。

（3）选择适当的运动链进行机构变换，定性分析机构运动以确定取舍 见第3章表3-3，选取组合序号为F1A、F1C-1、F1C-2、F1F-3的运动链进行机构变换，如图5-25所示。图中的T表示该副变换为移动副，机构图中标注有两个符号的运动副表示运动链图中符号相对应的两副构成的复合铰链；运动链图中标有HS的构件表示机构图中变换为高副。查看各机构的刀刃轨迹图，确认均满足生产工艺要求的动作。现定性分析各方案的运动。

1）曲柄滑块机构飞剪。如图5-26a所示，以AD为机架，CD为滑块，D为移动副T（图5-26b），上、下刀刃分别装在曲柄、滑块上（图5-26c）。

装在曲柄上的上刀刃作圆周运动，装在滑块上的下刀刃作直线运动。故该方案满足上、下刀刃运动轨迹之一应为封闭曲线的运动要求。其最大的优点是结构简单。但也存在突出缺点。①横向尺寸大。若偏距e大、连杆长度BC短将使机构压力角增大。为减小压力角α，需增大连杆长度BC。②调节钢材尺寸困难。若调短钢材尺寸，必须提高曲柄转速以减小每次剪切的时间。为使刀刃速度与钢材速度υ_t同步，同时必需减小曲柄半径AB和刀刃E的转动半径AE（图5-26d中的AB′、AE′）。由于剪切点由点K上移到K′，因此必须将钢材抬起方能进行剪切，这是不允许的。因此方案不可行。可见上刀刃不能装在曲柄上（装在连杆上影响较小）。

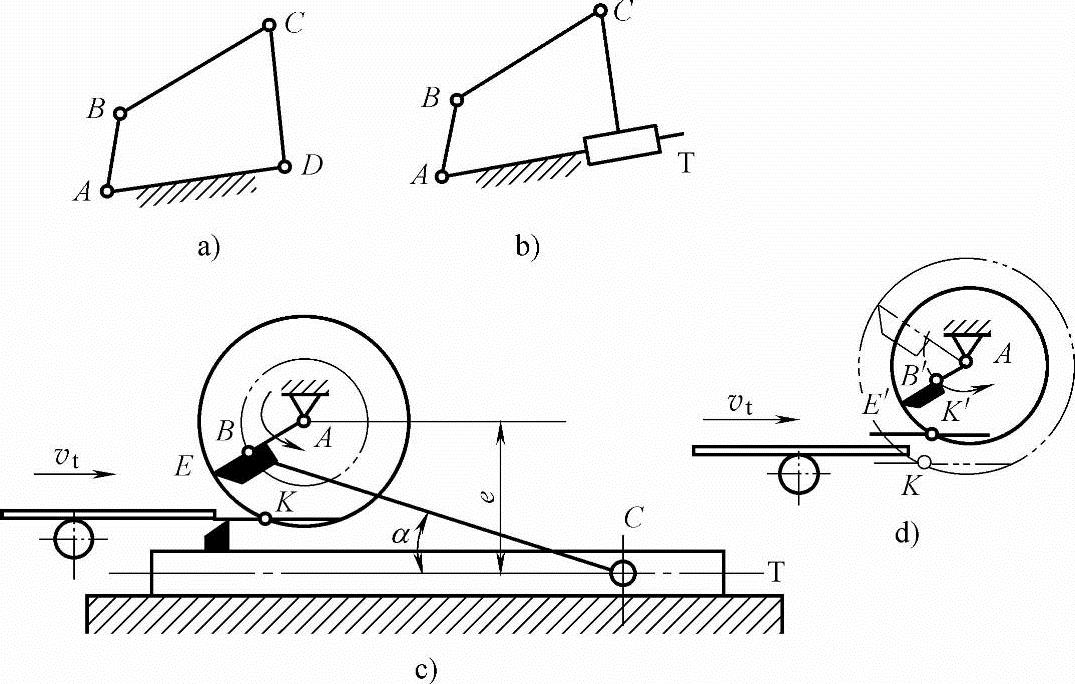
图5-26 曲柄滑块机构飞剪

2）铰链四杆机构飞剪。如图5-25所示方案2，该机构结构简单，重量轻，加工制作容易，刀刃轨迹满足工艺要求。若上下刀刃的速度满足剪切钢材的要求将是一个很好的选择方案。

3）方案3、4、5。三个方案的刀刃轨迹满足机构的动作要求，其突出优点是上下刀刃剪切时沿钢材方向的速度误差很小，设计难度小。特别是方案3的刀刃速度误差为零。但由于滑块加工的难度和成本较高，从而降低了其择优的几率。

4）方案6、7。分别为6杆机构和8杆机构。杆件多、重量大是其突出的缺陷，但其上下刀刃轨迹对称而使得其速度的误差和同步性最佳。方案缺点突出，特点鲜明令人难于割舍。若结构简单的结构能满足生产工艺要求，只能放弃方案6、7。

（4）初步拟定机构的尺寸定量地分析机构的运动，计算选定机构的运动参数，比较甄别出最佳机构。

1）机构给定的已知条件。

钢材运行速度υ_t=2m/s。

钢材定尺：L=1m。

刀刃重合度：Δh=5mm。

曲柄旋转速度：ω₁=2πn₁=2πυ_t/L=2π×2m/s/1m=4π/s。

拉钢系数δ=1.025。

上下刀刃沿钢材运行方向的速度误差：Δυ_C＜0.05。

机构尺寸参数计算的首要问题是确定曲柄半径a，曲柄半径的大小决定了刀刃的速度。因此，曲柄半径要根据上下刀刃运动和钢材运动共同确定。上下刀刃重合时的曲柄位置角φ⁰₁称为剪切角。

2）正弦飞剪机构的设计。建立机构设计的计算模型如图5-27所示。e、f为由刀刃安装确定的结构尺寸。机架结构尺寸d为曲柄转动中心到机架滑道中心的距离。首先由刀刃的速度求出曲柄半径a。

①运动分析。

刀刃E的位置方程

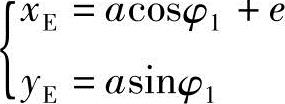
刀刃E的速度方程

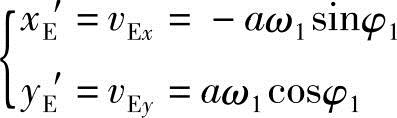
剪切角φ⁰1

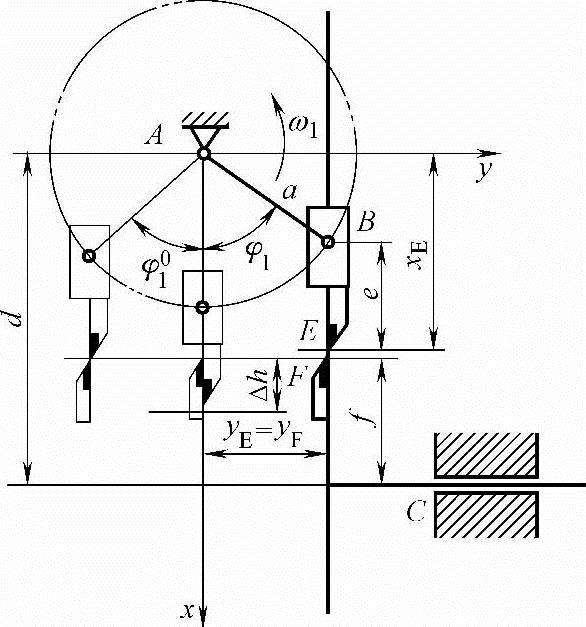
图5-27 正弦机构飞剪计算模型

cosφ⁰₁=（a-Δh）/a

②尺寸计算。

要求开始剪切时的刀刃速度y_E′为δυ_t，由此得

δυ_t=aω₁cosφ⁰₁=aω₁[（a-Δh）/a]

则a=δυ_t/ω₁+Δh=1.025×2000/（4π）mm+5mm=168.1338mm

因为cosφ⁰₁=（a-Δh）/a=（168.1338-5）/168.1338=0.97026，得

φ⁰₁=14.008°

若取e=f=250mm，则由图5-27可得

d=a+e+f=Δh=168mm+500mm-5mm=663mm

③校验机器性能。

刀刃剪切速度：

x_E′=υ_Ex=-aω₁sinφ₁=-168.1338×4πsin（-14.008°）mm/s=511.4265mm/s

y_E′=υ_Ey=aω₁cosφ₁=168.1338×4πcos（-14.008°）mm/s=2050.0001mm/s

拉钢系数：δ=υ_Ey/υ_t=2050.0001/20000=1.0250。

速度误差：由于y_E=y_F所以Δυ_C=0。

3）摆动导杆飞剪机构的设计

①运动分析

如图5-28所示，位移方程：

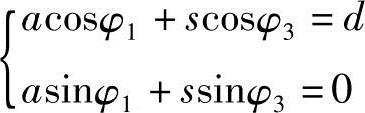
由此得：

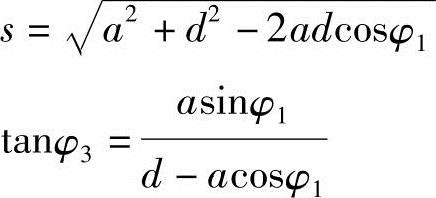
速度方程：

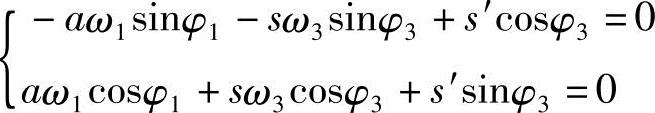
解得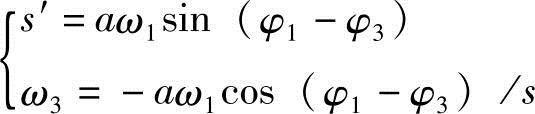

刀刃位置：

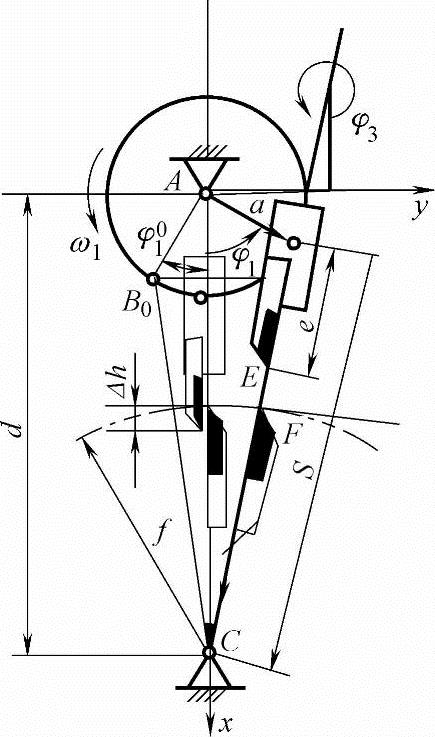
图5-28 导杆机构飞剪计算模型

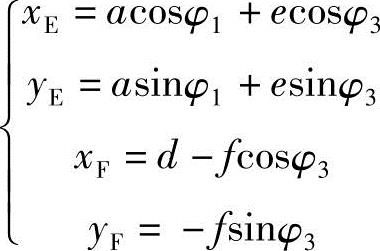
刀刃速度：

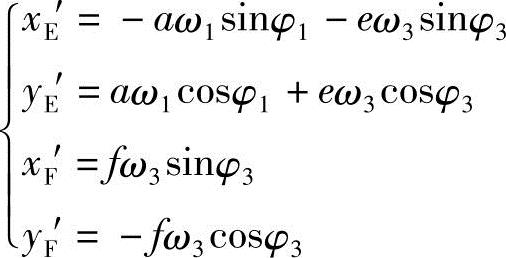
②机构尺寸设计。已知刀刃结构尺寸e、f。

按φ₁=φ⁰₁剪切时上下刀刃的速度与钢材运行同步求解曲柄半径a，即：

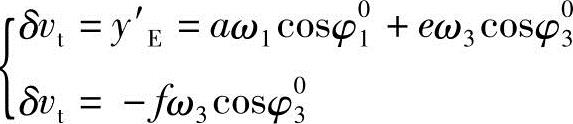
联立求解得

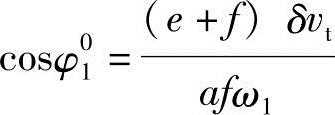
剪切时φ₁=φ⁰₁，由△AB₀C得

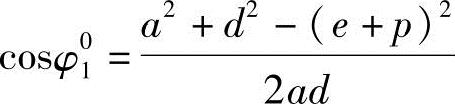
式中，d由下式确定：

d=a+e+f-Δh

设ρ=e+f，由以上两式联立并将d、ρ代入得

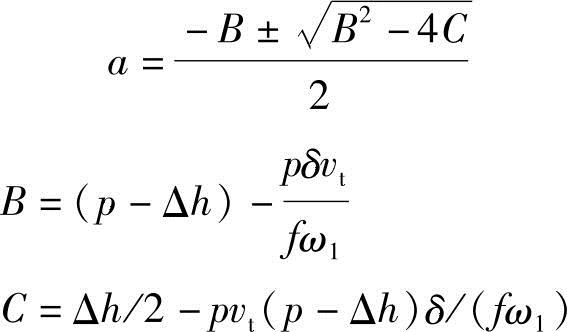
求出a后，再求d和摇杆摆角，得

sin（ψ/2）=a/d

③计算实例。令e=f=250mm，ρ=e+f=500mm。计算曲柄半径。

先求系数B、C，有

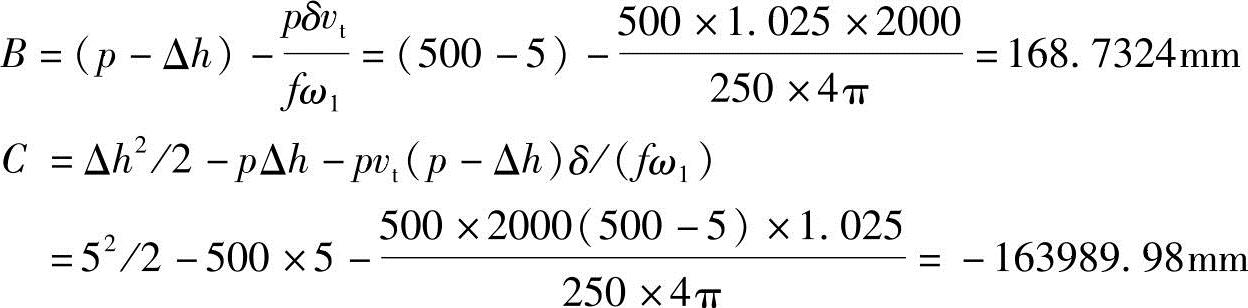
得

(www.xing528.com)

计算机架结构尺寸d。

d=a+e+f-Δh=329.2854+250+250-5=824.2854mm计算剪切角φ⁰₁。

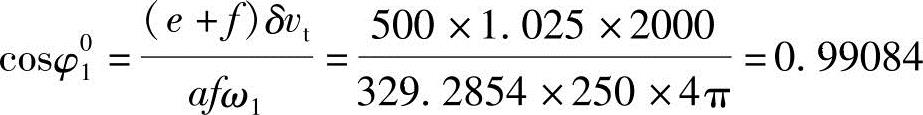
得φ⁰₁=7.76294°

计算摇杆摆角。

ψ=2arcsin（a/d）=2arcsin（329.2854/824.2854）=47.0913°

④校验机器性能。刀刃剪切速度误差：

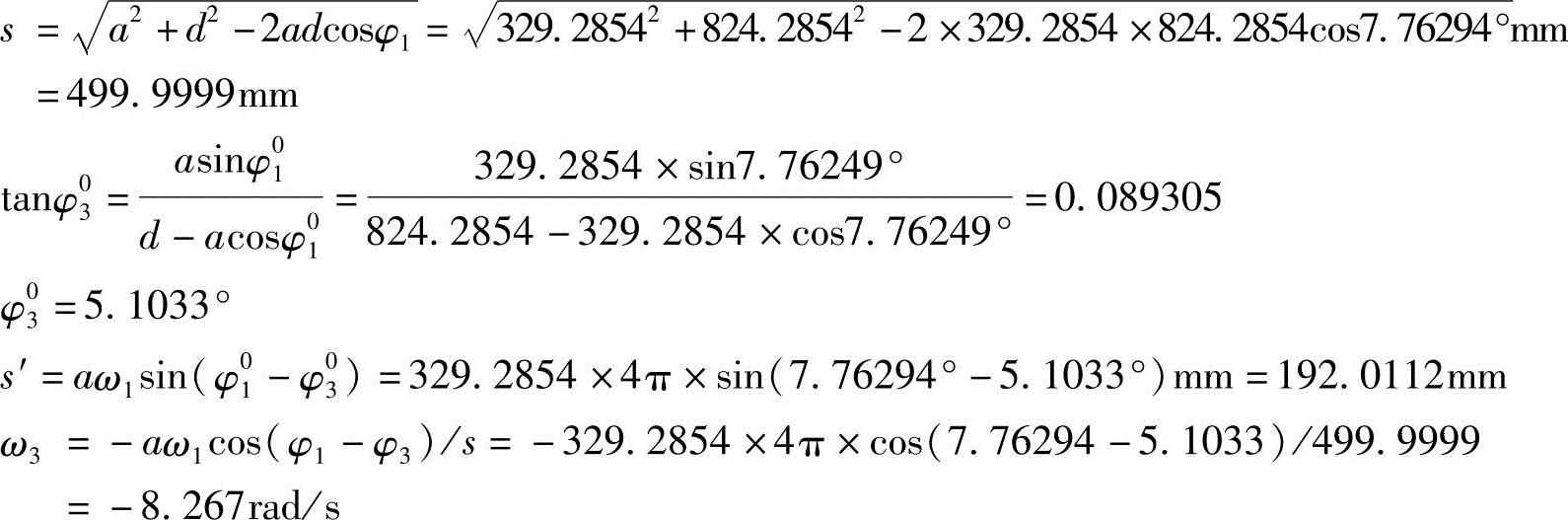
y′_E=aω₁cosφ⁰₁+eω₃cosφ⁰₃=329.2854×4π×cos7.76294°+250×（-8.267）×cos5.1033°mm/s=2041.4428mm/s

y′_F=-fω₃cosφ⁰₃=-250×（-8.267）cos5.1033°mm/s=2058.5573mm/s

v_C=（y′_E+y′_F）/2=（2041.4428+2058.5573）/2mm/s=2050.0000mm/s

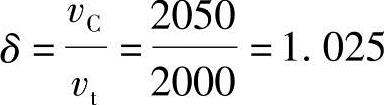
Δv_C=y′_E-y′_F/v_C=2041.4428-2058.5573/2050=0.008

4）铰链四杆飞剪机构的设计。设计分析思路：

设计分析思路：铰链四杆飞剪机构为最经济实用的一种机构。分析计算前应考虑两个因素：第一该机构应能满足剪切时剪切运动与钢材运动同步。第二应考虑机构的传力性能，虽不能与正弦飞剪机构相比，但应力求较大的传动角γ和较小的结构尺寸。

①速度同步问题。确定曲柄半径及机构尺寸应解决两个问题：首先，剪切时上下刀刃沿钢材方向的瞬时速度分量完全相等。其次，剪切时上下刀刃沿钢材方向的瞬时速度分量要与钢材速度尽可能同步。

如图5-29所示，上下刀刃的速度可用如下矢量方程表示：

v_E=v_C+v_EC

v_F=v_C+v_FC

式中，v_EC、v_FC为刀刃E（F）相对C点的相对速度，其方向垂直于CE（CF）。若此时CE（CF）为水平线，则v_EC和v_FC无水平速度分量，上下刀刃的水平速度v_Ey、v_Fy即是v_C的水平速度分量，而必然相等。可见，只要调整机架位置角α₄使刀刃重合时的CE（F）线处于水平位置，则必有v_Ey=v_Fy。

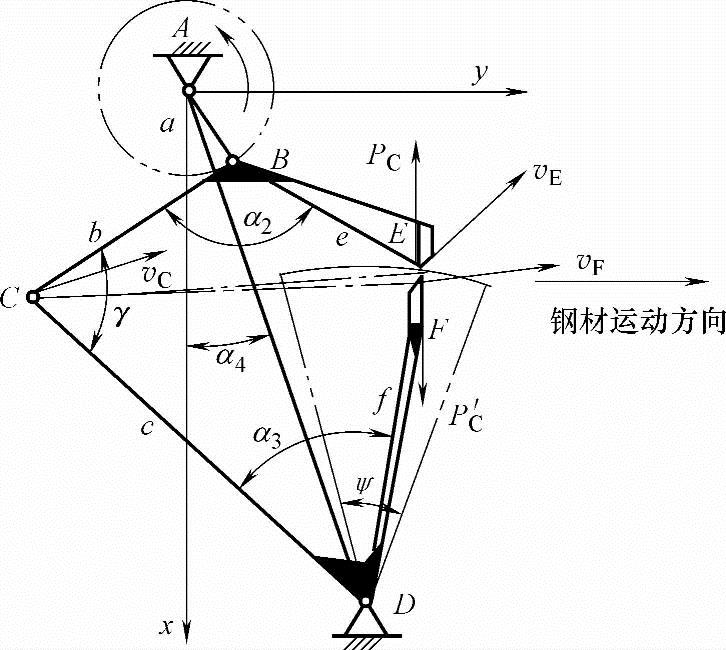
图5-29 铰链四杆飞剪机构

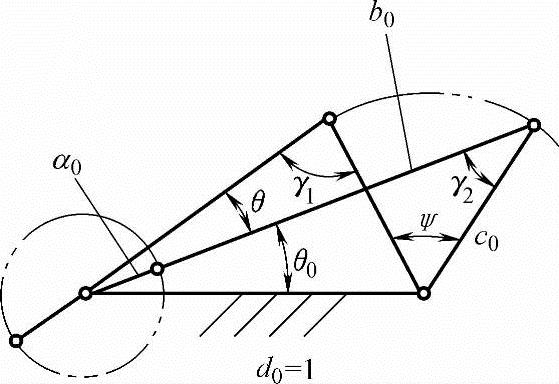
图5-30 四杆机构相对尺寸

②传力性能问题。由于要求刀刃速度与钢材运动同步，故其设计属瞬时运动量约束的机构综合，难以建立瞬时运动量与机构尺寸间的直接数学表达式，更难考虑机构尺寸设计时的传力性能。为此，先考虑传力性能求得机构的相对尺寸，然后再按速度同步要求确定机构的绝对尺寸。如图5-30所示，根据要求设定的机构传动角γ₂、摇杆摆角ψ和行程速度变化系数k，可保证机构的运动性能和传力性能。机构d₀=1时的相对尺寸表示为a₀、b₀、c₀。计算公式如下（详见第8章）：

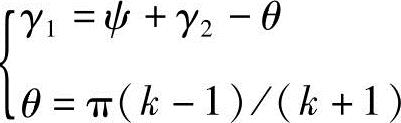
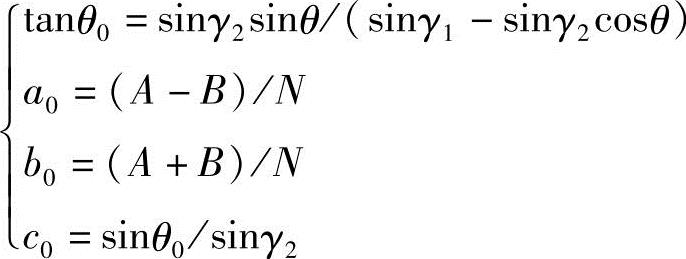
A=cos（θ+θ₀）sin（γ₂+θ₀）

B=sinγ₂+sinθ₀cos（γ₁+θ+θ₀）

N=2sinγ₂cos（θ+θ₀）

求出这些保证机构的运动性能和传力性能的相对尺寸后，再根据速度同步要求确定曲柄半径的绝对尺寸，最后各尺寸按比例放大即可。

机构的尺寸设计：机构尺寸的确定不像前两例直接求解那样简单，须经初步确定、计算检验、尺寸调整等过程反复进行。

①初定曲柄半径a。若曲柄销的速度为v_B，则曲柄半径a为a=v_B/ω₁。由于v_B与刀刃平均速度v_C并不相等，故曲柄半径不能仅根据曲柄销的速度精确决定。设k₁=v_B/v_C（k₁为曲柄销B点的速度v_B与刀刃平均速度v_C之比，取值1.2）。由v_C=δv_t得a=k₁v_tδ/ω₁。初步设计时k₁可任选，机构初步设计完成后再重新确定k₁。

②四杆机构的绝对尺寸。曲柄半径a求出后可按比例尺_μ=a/a₀得绝对尺寸：b=b₀μ，c=c₀μ，d=μ。

③刀刃位置确定。如图5-31所示，先设定机架角α₄（例如选择α₄=0°～3°），使曲柄a与机架d共线，按下刀刃位置DF垂直钢材运行方向来确定刀刃位置尺寸和刀刃重合量Δh。此时有v_Fy≈v_Ey且其方向与钢材运行一致。因为曲柄与机架共线时，连杆2和摇杆3的绝对瞬心均在D点且两者的角速度相等ω₂=ω₃。

若计算出f、α₃、e、α₂，即确定了刀刃F、E的位置。f、e用下列公式确定：

f=dcosα₄-h

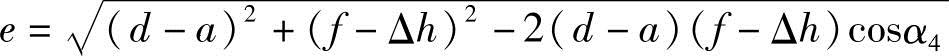
初步计算α₃、α₂：

α₃=α₄+Δα

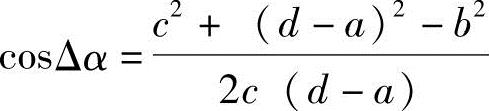
α₃求出后可由△CDE、△CDF分别求出l_CE、l_CF，此时l_CE≠l_CF。其实，剪切时点E、F应该重合，故试取l_CEF=（l_CE+l_CF）^/2，然后再由△BCE求出α₂：

l_CF=[c²+f²-2cfcosα₃]^1/2

l_CE=[c²+（f-Δh）²-2c（f-Δh）cosα₃]1/2

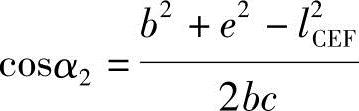
最后由△DCF按长度l_CEF、尺寸c、f重新修正计算α₃：

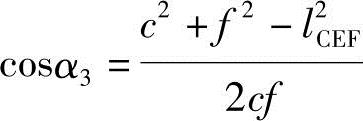
④剪切角φ⁰₁的确定。剪切角φ⁰₁即剪切时所对应的曲柄转角。由图5-32知：

φ⁰1=α₄-∠DAB

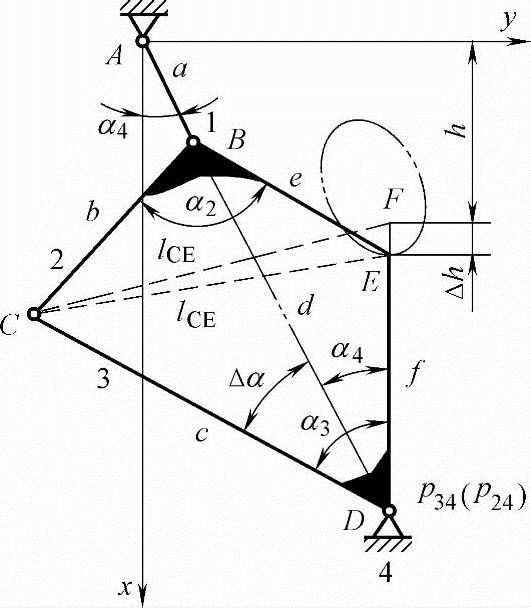
图5-31 刀刃位置尺寸

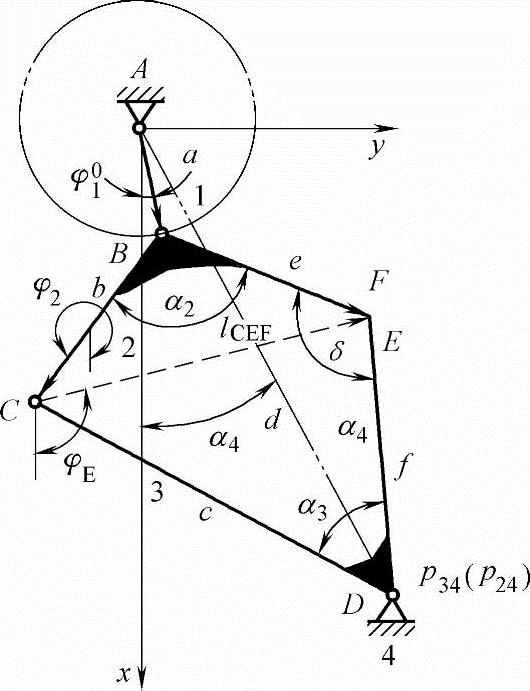
图5-32 剪切角确定

∠DAB由△ADB按余弦定理求解。

⑤调整上下刀刃水平速度误差。当曲柄转角φ₁=φ⁰₁时，飞剪对钢材进行剪切。此时若上、下刀刃E、F沿钢材运动方向的速度误差太大，则出现倾斜的钢材切口，甚至不能切断钢材。

如前所述，调整机架倾角α₄使CE（F）线处于水平位置可使上、下刀刃的速度误差为零。

先对机构进行运动分析求出φ₂（参考第2章），再由矢量多边形BE=BC+CE求解φ_E，得

ecos（φ₂+α₂）=bcosφ₂+l_CEFcosφ_E

esin（φ₂+α₂）=bsinφ₂+l_CEFsinφE

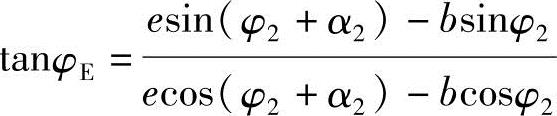
为使CE（F）线处于水平位置，必须使整个机构沿顺时针转动Δφ_E=φ_E-90°。按下式计算机构转动后的机架倾角α₄*和剪切角φ⁰₁*：

α₄^*=α₄-Δφ_E

φ⁰₁^*=φ⁰₁-Δφ_E

⑥调整刀刃与钢材运动速度。进行运动分析求上、下刀刃沿钢材方向的速度分量y_E′、y_F′后可求出上、下刀刃沿钢材方向的平均速度υ_C=（y_E′+y_F′）/2及拉钢系数δ。由于曲柄半径是按k₁初步选定的，一般δ不等于初始拉钢系数，即上、下刀的速度不满足预先选定的拉钢系数要求。由于曲柄转速不能调整，故应调整曲柄半径。应计算出实际的k₁^*=aω₁/v_C值后重新计算曲柄半径a*：

a*=k₁^*δL/（2π）

为保证原始给定参数γ₂、k、ψ不变，各长度尺寸应按比例尺μ_l=a^*/a作等比缩放，得到最终机构尺寸：b^*=b_μl，c^*=cμ_l，d^*=dμ_l，e^*=eμ_l，f^*=fμ_l。由此得到满足给定设计要求的机构尺寸，其剪切角为φ⁰₁^*。

求曲柄的平衡力矩M_b。已知剪切力P_C，求出上下刀刃沿剪切方向的速度x_E′、x_F′后，即可按机构上各外力（矩）的瞬时功率平衡原理求出作用于曲柄上的平衡力矩：

M_bω₁-P_Cx_E′+P_Cx_F′=0

M_b=P_C（x_E′-x_F′）/ω₁

选择不同参数的设计方案比较。

①α₄⁰=0°时，不同给定参数飞剪设计结果，见表5-3。

表5-3 α⁰₄=0°时不同给定参数飞剪设计结构

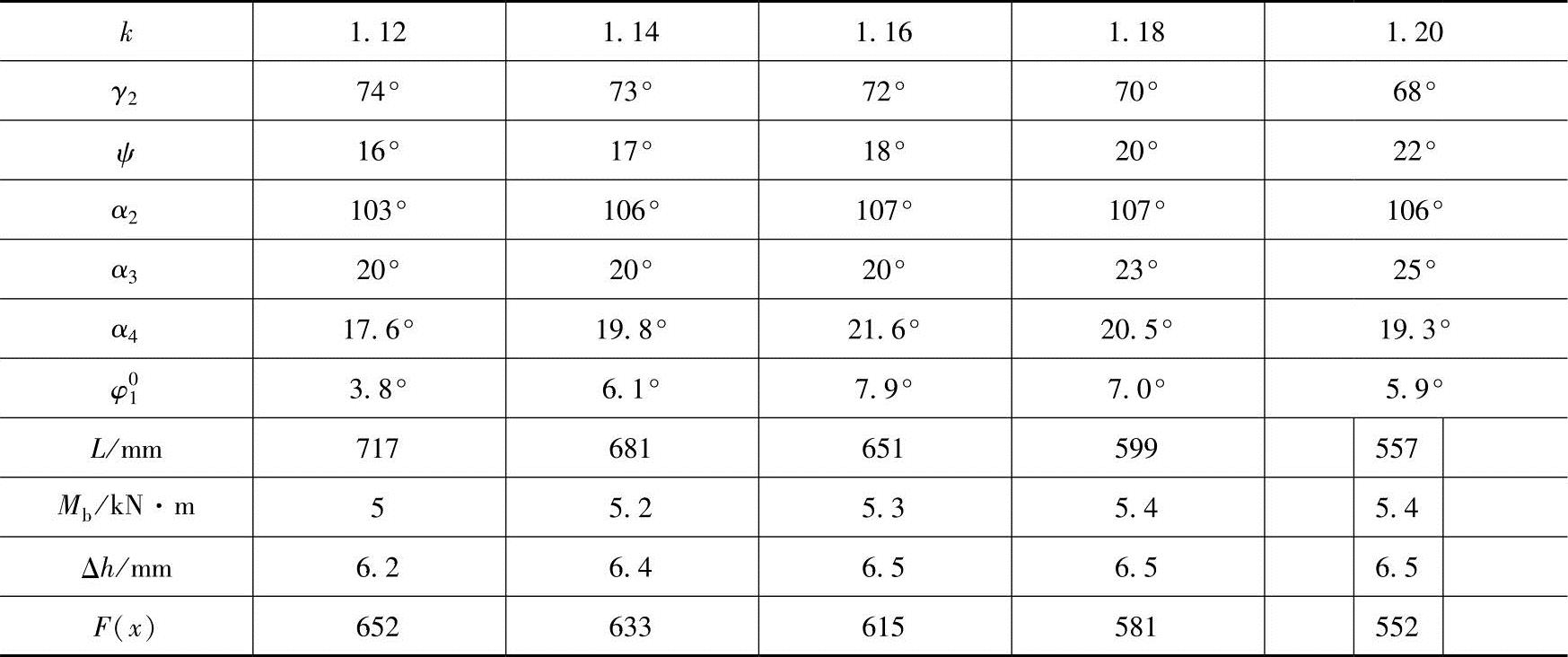
注：平均杆长为L=（a+b+c+d+e+f）/6；

功耗尺寸当量值为F（x）=30M_b+0.7L。

可见，当k=1.20时有较小的功耗尺寸当量值F（x）。

②不同α⁰₄时飞剪设计结果，见表5-4、表5-5。

表5-4 k=1.2、ψ=22°、γ₂=68°时飞剪设计结果

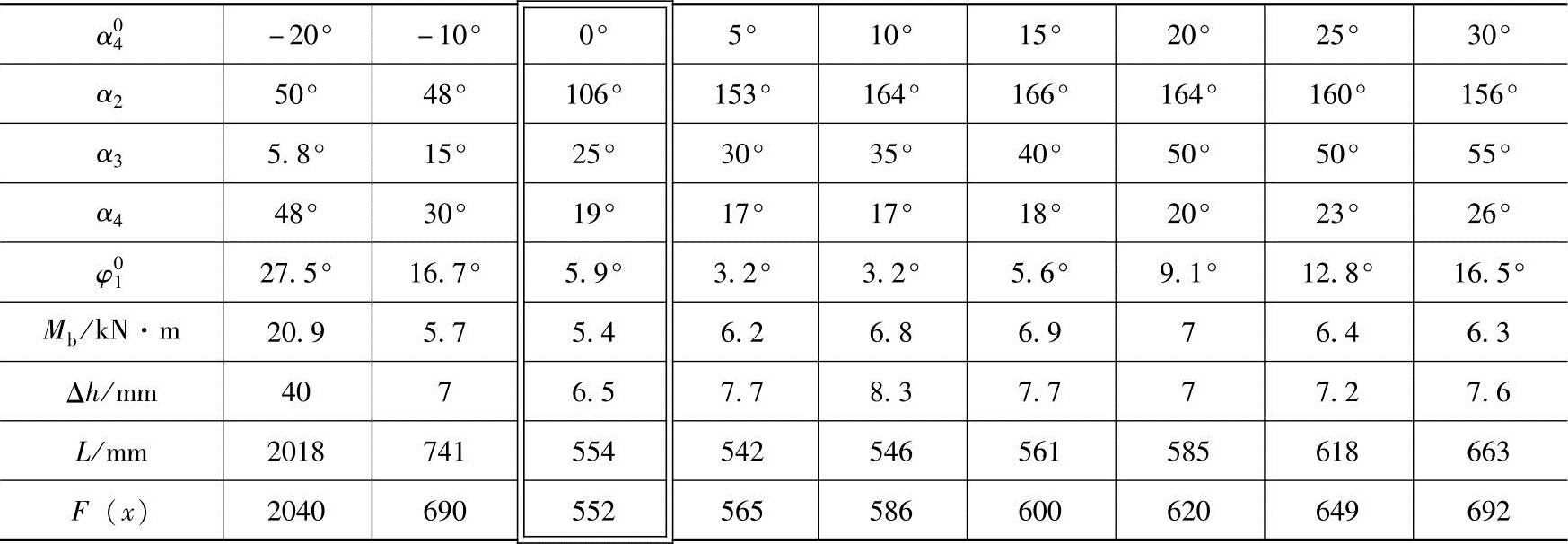
可见，k=1.2、ψ=22°、γ₂=68°时，取α₄⁰=0°有较好的设计结果。

表5-5 k=1.12、ψ=16°、γ₂=74°时飞剪设计结果

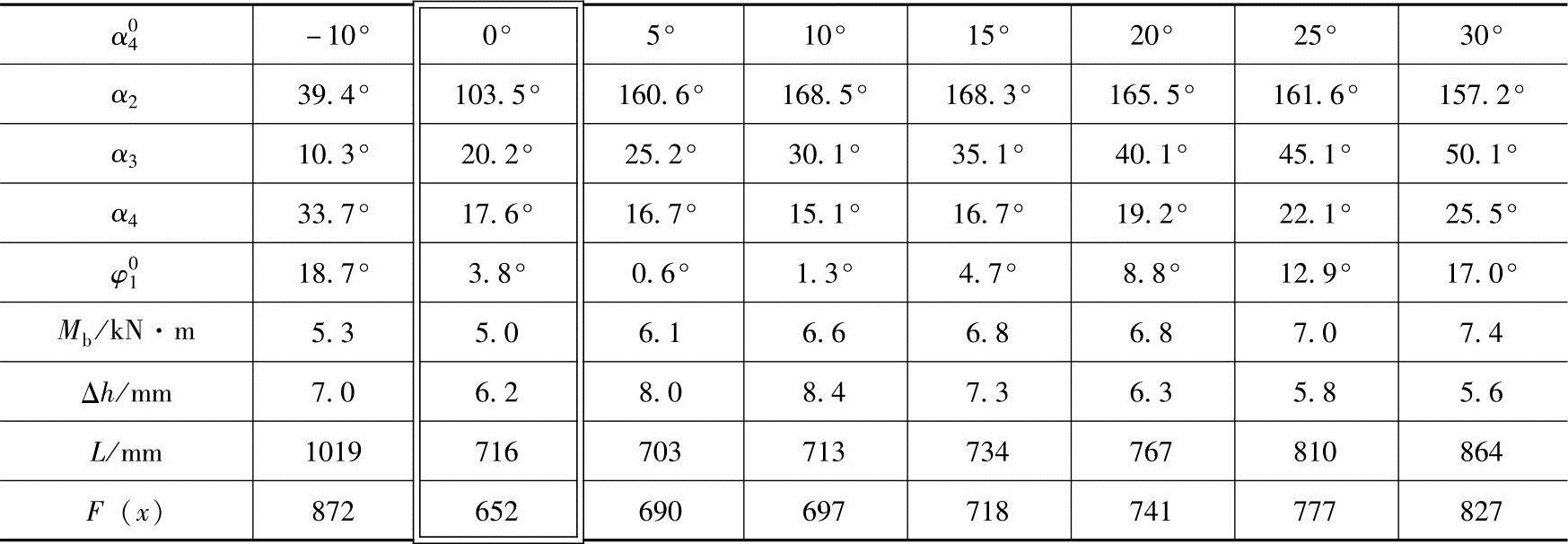
可见，k=1.12、ψ=16°、γ₂=74°时，取α⁰₄=0°有较好的设计结果。

③设计方案参数选择。从以上各方案计算结果发现，保持原有的k、Ψ、γ₂参数值不变的情况下，k₁值可任选。k=1.2、α⁰₄=0°的设计方案有较好的机构性能。

④摆动导杆飞剪机构设计的计算机程序。

对（K（行程速度变化系数），gama2（远极位传动角），pusai（摇杆摆角），la（拉钢系数），k1（曲柄销与刀刃速度比值），afa4（机架倾角），dw（曲柄圆分点数））参数赋值后即可得到计算结果：

输出结果：result（速度校正后的结果），fai1（剪切角），a、b、c、d（机构尺寸）、afa4（机架倾角），e、afa2、f、afa3（刀刃位置参数），vet、vft（刀刃水平速度），Utpoint（输出的性能参数），xe、ye、xf、yf（刀刃坐标值），vex、vfx（刀刃垂直速度），Vdao（刀刃平均速度），dtadao（上下刀刃剪切时的水平速度误差），la（拉钢系数），mb（曲柄输入力矩）。

以下为源程序及其运算结果：

程序运行结果如下：

⑤机构各方案比较。定性分析后筛选出的三个方案均为四杆机构，其比较见表5-6。

表5-6 机构方案比较

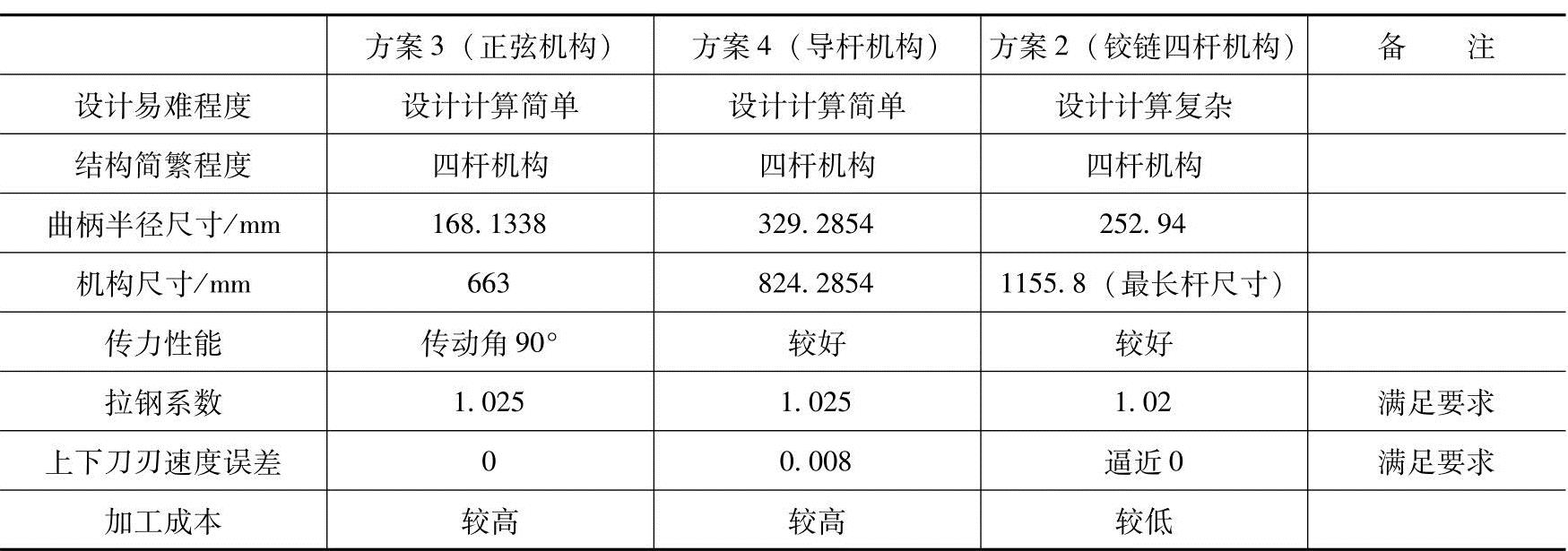
从表5-6中可见，三个方案均为满足生产工艺的上佳方案，但各有优劣。方案3、4具有结构小巧、重量轻等优点，但加工成本较高；而方案2结构较大但加工成本较低。可根据实际条件及不同的要求，因时因地加以选取。