变胞机构变胞点判别计算及运动程序

1.机构的变胞点

变胞点分显形变胞点和隐形变胞点。

显形变胞点为机构中促使机构构型和机构自由度改变的可见物件。

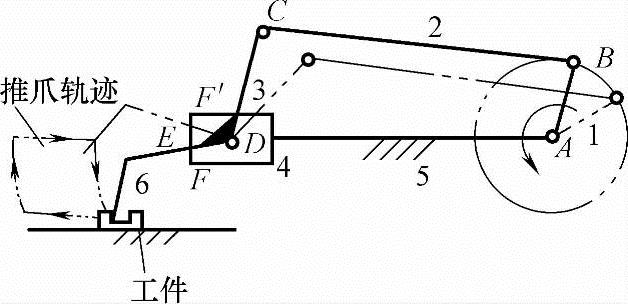
图5-15 运动自调推料机

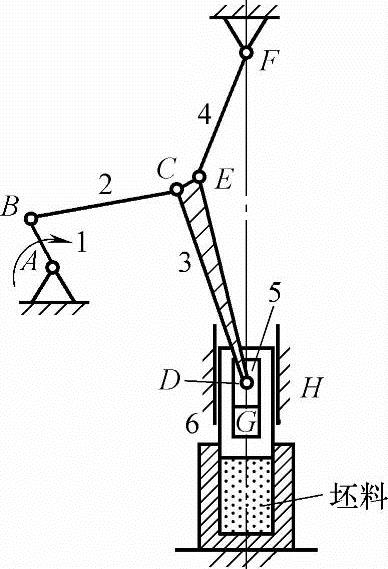
图5-16 砖坯压制机构

如图5-15所示运动自调推料机构中的挡块F、F′即显形变胞点，当连杆3不与挡块接触时，机构自由度为2；当连杆3与挡块接触使得3与滑块成为一体时，机构自由度为1。机构主动件沿逆时针方向转动（如虚线位置）时，推爪6按所示轨迹运动，自动完成“抓住工件、向左移送工件、推爪向上脱离工件、摇杆3和滑块4成为一体向右运动”的动作。如此反复运动将一个个工件推向左方。此机构适用于推送轻型工件，其机构简单紧凑。

隐形变胞为机构中促使机构构型和机构自由度改变的非可见瞬时位置点。如图5-16所示砖坯压制机构，滑块5、6间可相互滑动，机构自由度为2。但机构每一个运动阶段的运动是确定的，其运动顺序为“滑块5、6构成一体向下运动→滑块6靠自重轻压坯料→坯料的反力与滑块6重量相等时滑块5在滑块6中移动→滑块5达到滑块6底部时成为一体压实坯料”。坯料的反力与滑块6重量相等时的机构位置即机构的隐形变胞点。运动中压砖工艺要求的“轻压以排除坯料中的空气、再压实成型”的两步作业由机构自动完成。

又如控制两个制动杆的两自由度机构，两个制动杆是按前后顺序还是反复交替运动取决于机构的瞬时受力情况；再比如汽车驱动轮的差动轮系，其自由度为2。但每瞬时该轮系按普通轮系还是按差动轮系运动取决于汽车在直道还是弯道上行驶。

由此可见，显形变胞点和隐形变胞点在同一机构中可能同时存在并相互转化，且两种变胞点是否能相互转化与机构的受力情况有关。因此判别机构中是否存在变胞点，何时出现变胞点是确定机构是否按预定顺序运动的关键。

2.机构变胞点的判别方法

一般情况下机构的显形变胞点容易判断，关键在于如何判断机构自由度大于1时出现隐形变胞点的时间。对于显形变胞点采用该点与干预构件间距离最小准则来判别；对于隐形变胞点运用最小耗功原理，即机构向阻力最小的方向运动原则来判别。其具体方法是，若机构瞬时自由度大于1，将机构转化为与自由度相等数目的单自由度机构，分别对各单自由度机构进行运动分析和力分析，然后根据两种判别方法确定哪个单自由度机构的运动是该多自由度机构的运动。将机构主动件的运动行程分为若干等分，反复以上判别方法即可确定变胞机构的整个运动程序。大致步骤如下：

1）在显形变胞点的干预下计算确定机构的初始位置（此时机构自由度为1）。

2）将机构主动件的行程分为若干等分，主动件增加一小位移，判别为主动件位移：若位移与行程相等，转到6。

3）根据多自由度机构的几种运动可能性，分别固定某个（或几个）构件为机架，得到与机构自由度数目相等的若干单自由度机构。

4）对各单自由度机构进行运动分析和力分析。

5）对变胞点进行判别：

①比较各单自由度机构的主动件的驱动力，驱动力最小的单自由度机构的运动即该多自由度机构的瞬时运动。

②计算驱动力最小的单自由度机构中的运动构件与显形变胞点间的距离，距离较大时表示机构构型不变，转到步骤2。若距离较小，则改变主动件位移增量的大小与方向，使距离值逼近最小值，此即改变机构构型的位置，转到步骤2。

6）终止计算。

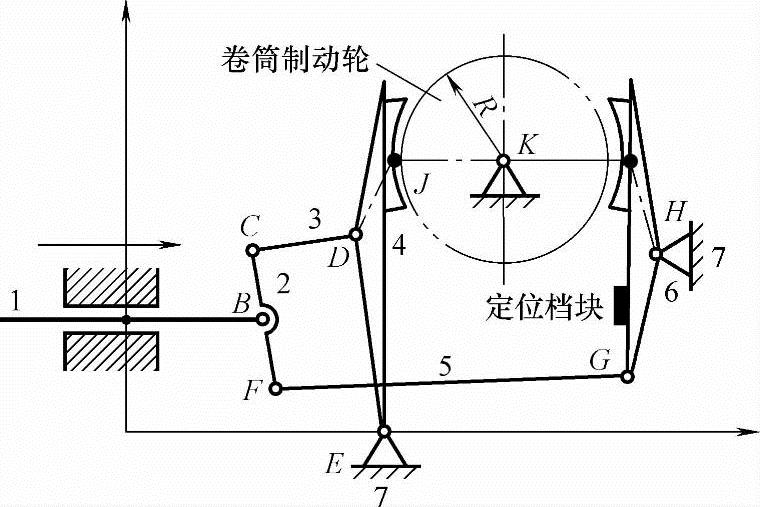
图5-17 大型升降机卷筒制动机构

3.变胞机构运动程序计算实例

（1）升降机的制动机构工作原理 如图5-17所示为大型升降机卷筒制动机构，要求具有很高的安全性。例如用于矿山竖井中的载人罐笼升降机，其制动系统是采用液压操纵的庞大的多杆机构，能够实现准确的制动要求。若采用F=1的机构使左右制动杆4、6制动瓦同时抱住制动轮，很难避免因某种误差导致单边制动瓦接触或左右两制动瓦接触不均的现象。因此采用如图5-17所示的F=2的七杆低副机构。该机构避免了机构左右制动杆4、6的跑偏现象，尽管制动杆的微观运动是随机的，但可依照最小耗功原理有序进行。而制造、安装乃至磨损等引起的运动误差只可能改变微观运动的顺序而不会改变两制动瓦先后接触并最终抱紧制动轮这一运动的最终结果。

松开制动时，用定位挡块限制机构的初始位置，该挡块即显形变胞点；用左右制动杆4、6制动瓦上的点J、点I，以判定制动瓦是否与制动轮接触。故该机构有三个变胞点：挡块、点J、点I。机构自由度为2时运动中的变胞位置由计算确定。

（2）机构的运动分析 已知机构的运动简图参数如图5-18所示。

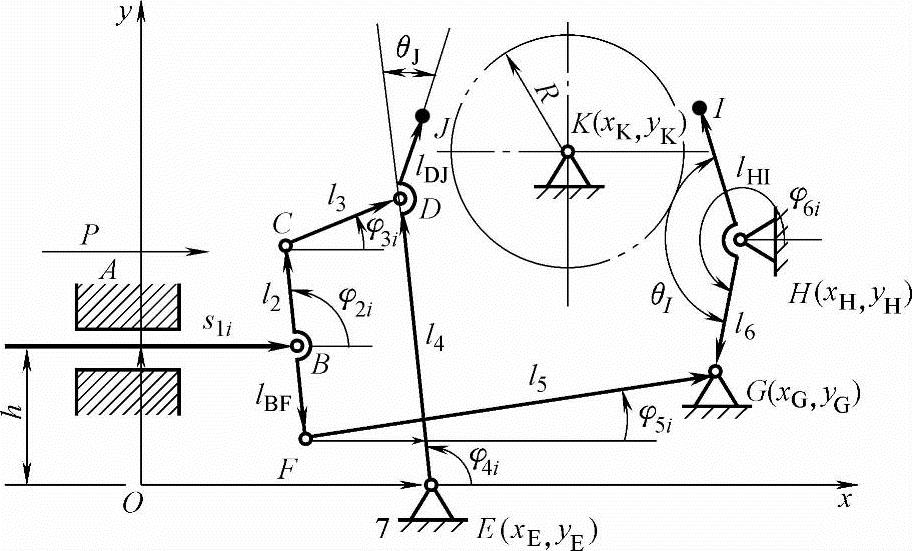
图5-18 机构的初始位置图（AEG机构）

1）机构的初始位置。由于挡块的定位，可将制动杆6视为固定的机架（G点坐标已知）。此时由构件1、2、3、4、5和机架7构成的六杆机构F=1。

由OABCDEO和OABFGO两个回路建立的坐标方程式（5-3）可解出机构初始位置的待求量φ_2i、φ_3i、φ_4i、φ_5i。

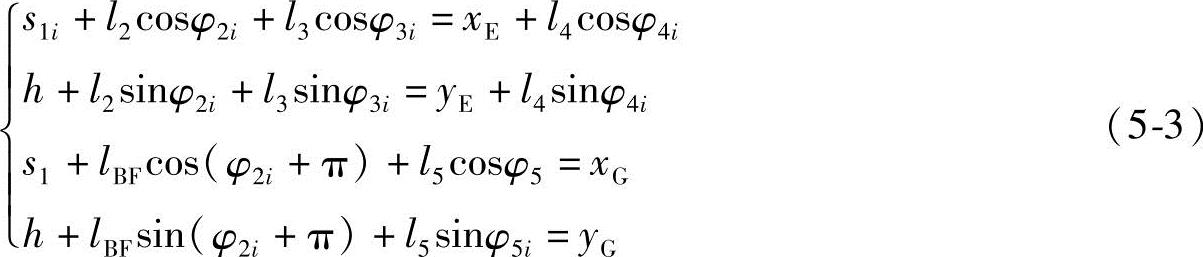
计算D点的位置坐标：

2）单自由度机构的运动分析。通过机构初位置计算已求得G、D的坐标值。由于机构F=2，设主动件的行程为h，主动件的位移为s_1i=s₁₀+Δs_i（i=1，2，…，n；Δs_i=h/n），此时机构的位置不能确定。为此将机构转化为两个自由度为1的单自由度机构，即分别将G、D固定为机架，得到两个单自由度机构。用机架标号表示所属机构分别为机构AEG和机构ADH，即：机构AEG表示右制动杆不动，左制动杆运动；机构ADH表示左制动杆不动，右制动杆运动。

①机构AEG的运动分析。只需将

s_1i=s₀+Δs_i（i=1，2…，n） （5-5）

代入式（5-3）即可求出机构该位置的φ_2i、φ_3i、φ_4i、φ_5i。

由式（5-4）求出机构该位置的D点坐标x_D、y_D。

变胞点J的位置：

制动轮中心K距J点的距离：

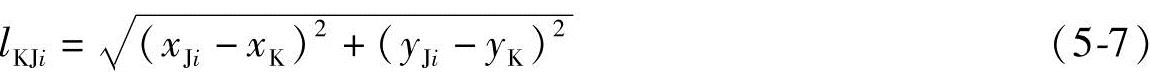
若主动件的速度为v₁，i构件的角速度用ω_i表示，式（5-3）对时间求导得

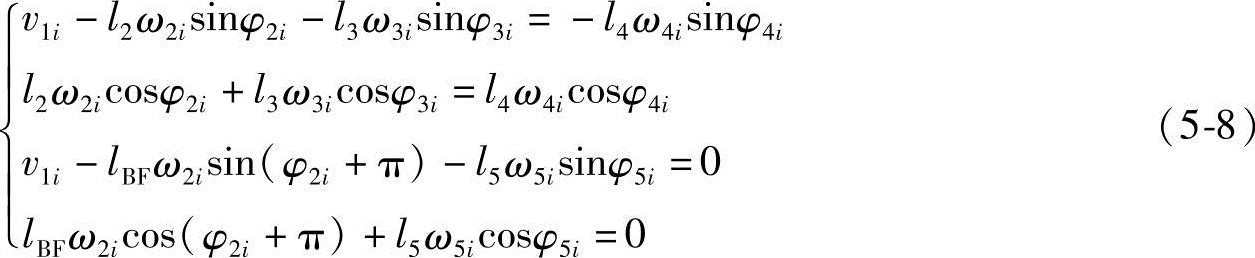
利用式（5-8）可求出ω_2i、ω_3i、ω_4i、ω_5i。

②机构ADH的运动分析。如图5-19所示，D点坐标值已由式（5-3）求出，并视其为固定支座。由OABCDO和OABFGHO两个回路建立的式（5-9）可解出机构该位置的待求量为φ_2i、φ_3i、φ_5i、φ_6i。

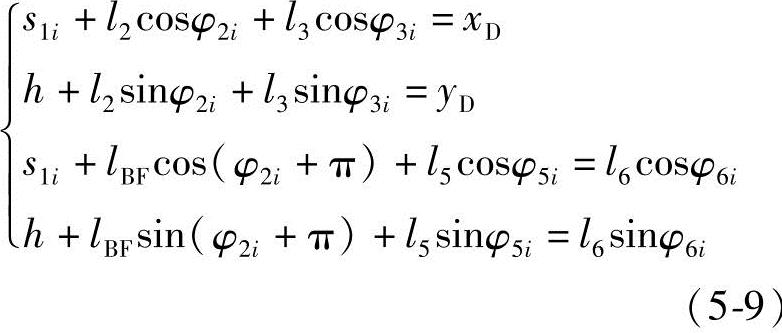
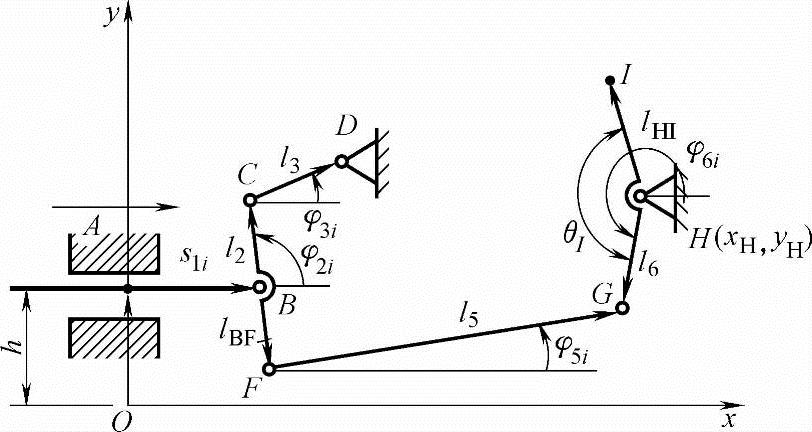
图5-19 ADH机构位置图

变胞点I的位置：

(www.xing528.com)

KI两点间的距离：

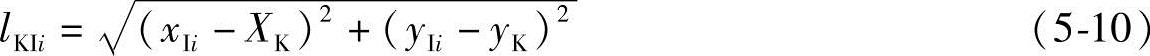
计算G点的位置坐标：

式（5-9）对时间求导得

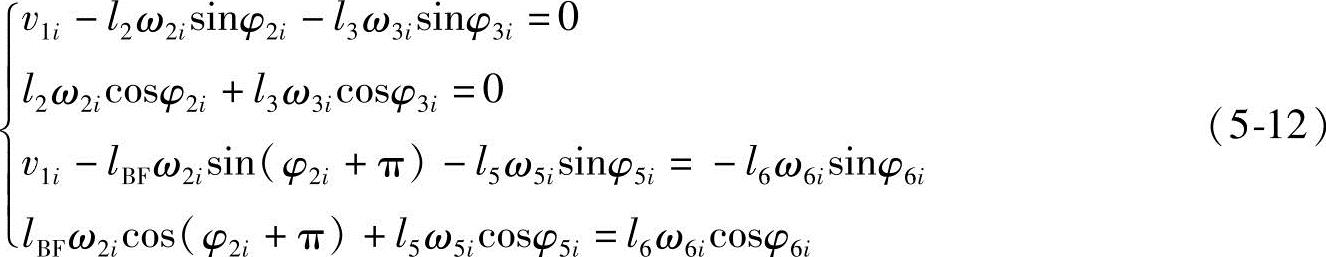
利用式（5-12）可求出ω_2i、ω_3i、ω_5i、ω_6i。

（3）机构的力分析 如图5-18所示，该机构主动件的驱动力用以克服由左右制动杆的自重以及各运动副中的摩擦力以及摩擦力矩产生的阻力。若其他各杆自重较小并略去，则杆3、5为二力杆。

将构件i对构件j的运动副反力记为R_ij，若大小、方向均未知时用其坐标的两个分量R_ijx、Rijy表示。运动副中除运动副反力外，还有摩擦力矩。构件i对构件j的摩擦力矩为

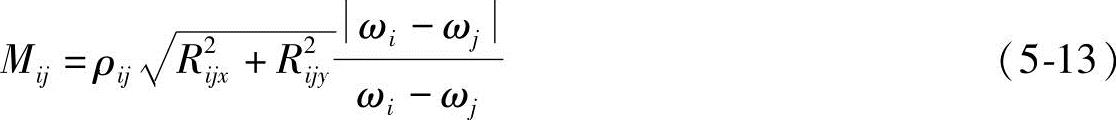
式中，M_ij的方向与ω_i-ω_j/（ω_i-ω_j）确定的正负号一致；ρ_ij为构件i、j构成的转动副的摩擦圆半径。

由上可见，引入摩擦力矩使得力分析方程式成为运动副反力的非线性函数，给方程组的求解带来困难。为此将式（5-13）线性化，即将上式在不计摩擦（R_i（_jx⁰），R_i（_jy⁰））处展开成泰勒级数并只保留其线性项，得

M_ij≈K_ijx^（0）R_ijx+K_ijy^（0）R_ijy （5-14）

式中常数项为

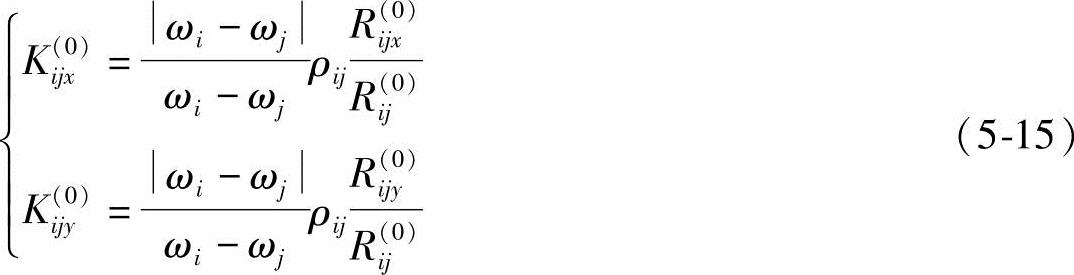
现分别对AEG、ADH两个单自由度机构进行力分析。

1）AEG单自由度机构的力分析。如图5-20a所示，G₄为左制动杆的重量，其作用点M₄位置用l_M4、θ_M4表示。取二杆组CDE和ABCF作受力分析，如图5-20b、c所示。

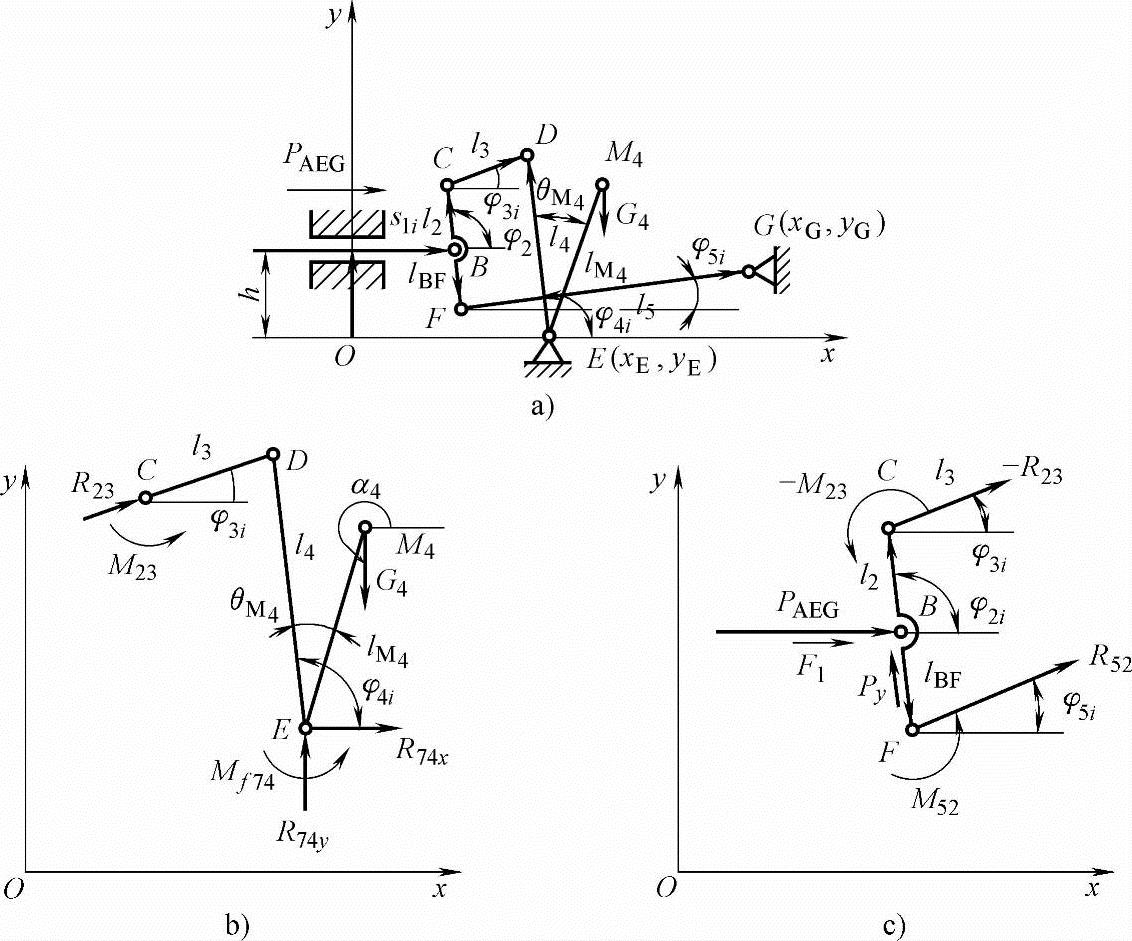
图5-20 AEG机构力分析图

a）AEG单自由度机构 b）CDE杆组力分析模型 c）ABCF杆组力分析模型

二杆组CDE力分析：

构件4由∑x=0，∑y=0，∑M=0得

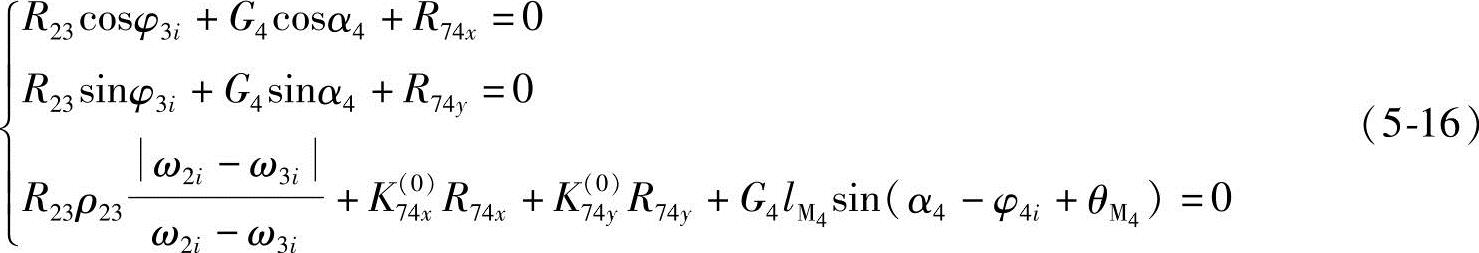
由构件3得

R₂₃=R34

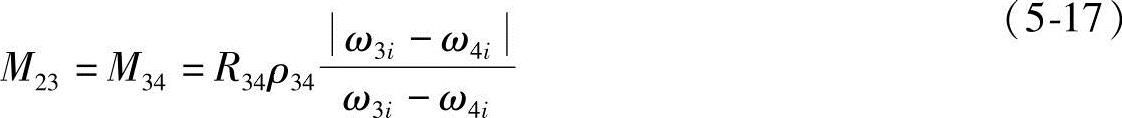
二杆组ABCF力分析：

图5-20c中，P_AEG为单自由度机构AEG主动件的驱动力，P_y为主动件移动副中的正压力，由其产生的摩擦力为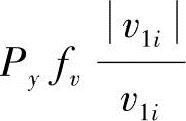，fυ为移动副处的滑动摩擦因数。由∑x=0，∑y=0，∑M=0得

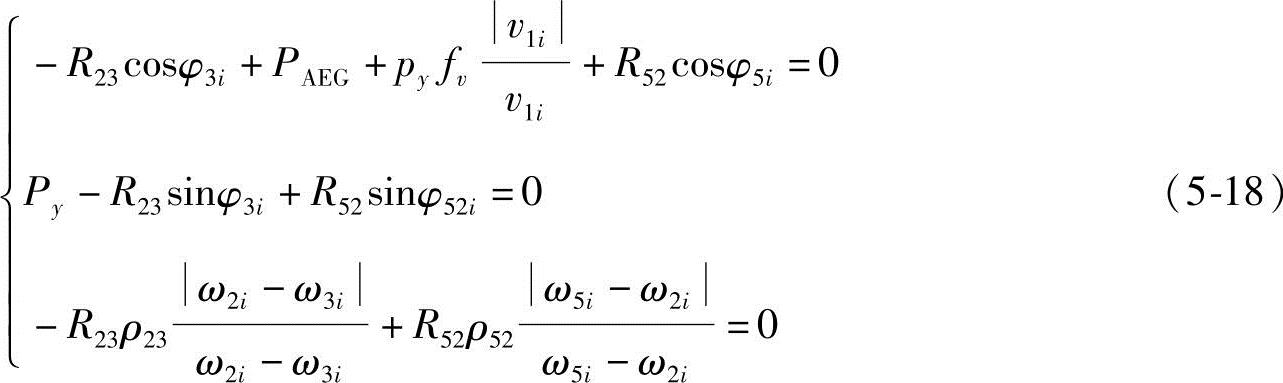
将式（5-16）、式（5-18）写成矩阵式：

（5-19）

对于上述线性方程组，先令ρ₃₄、ρ₇₄、ρ₂₃、ρ₅₂=0，得到不考虑摩擦的运动副反力R₃₄^（0）、R_74x^（0）、R_74y^（0）。然后令ρ_ij为给定值，由式（5-15）计算K_74x^（0）、K_74y^（0）。第二次求解式（5-19）得到考虑摩擦的运动副反力R₃₄、R_74x、R_74y、R₅₂、P_y及该单自由度机构AEG的驱动力P_AEG。

2）ADH单自由度机构的力分析。如图5-21所示，按以上相同方法可求得ADH单自由度机构的驱动力P_ADH。

（4）升降机的制动机构运动顺序确定 以上机构的运动分析和力分析为变胞点的确定提供依据。其判别方法为：

1）隐形变胞点判别。若P_AEG＜P_ADH，说明按单自由度AEG机构完成运动有较小的阻力，故该单自由度AEG机构的瞬时运动即为整体机构的运动（该状态用符号AEG=0，ADH=1标记）。

2）显形变胞点判别。单自由度机构运动过程中某显形变胞点参与干预时，其数学表达式：

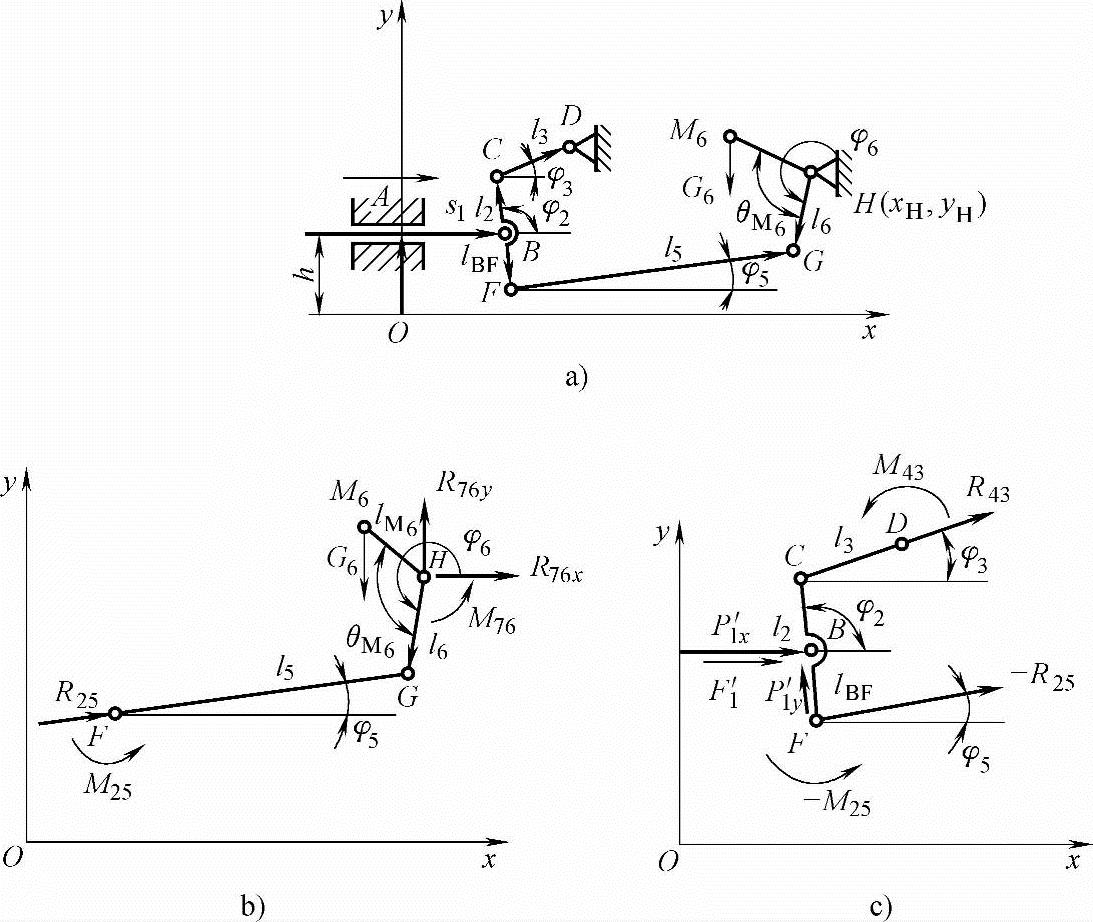
图5-21 ADH机构力分析图

a）ADH单自由度机构 b）FGH杆组力分析模型 c）ABCF杆组力分析模型

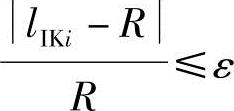
或（5-20）

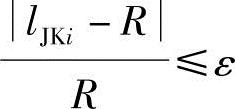
式中，ε为预定的收敛系数。

满足上式表明变胞点I或J与制动轮接触，则I或J停止运动。若不满足上式，则按下式减小主动件位移，直到满足式（5-20）为止。

s_1i=s_1i-kΔs_i （5-21）

式中，k为小于1的位移缩短系数（例如k=10^-3）。

其计算过程如图5-22所示。

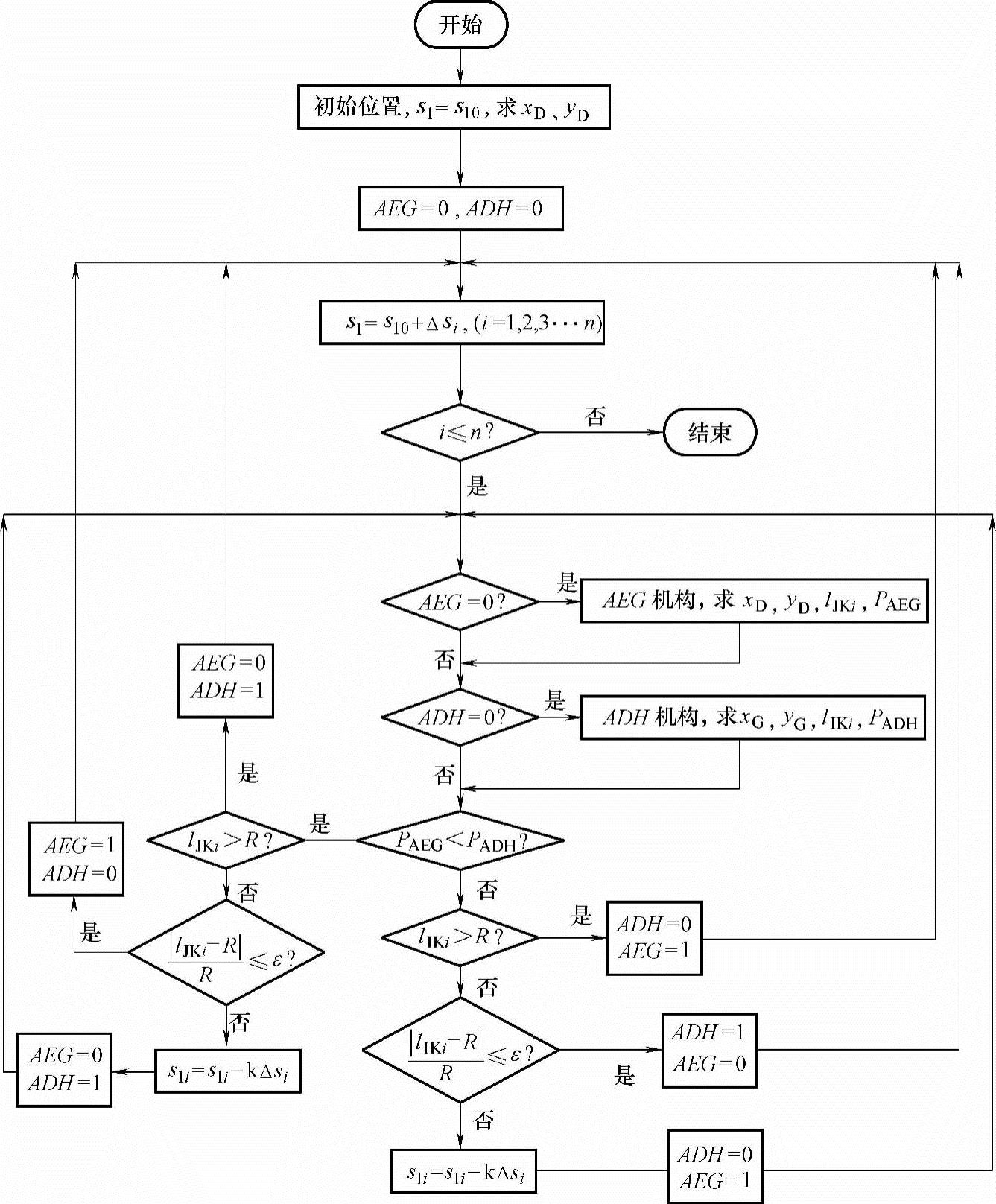
图5-22 升降机制动机构运动顺序计算框图