机构型综合的优化方法

根据运动副所具有的约束及其高副低代原则，在连杆组合分类分析中把移动副、高副均转化为转动副。在机构型综合中，如果对某选定的运动链进行上述过程的反演，并以不同构件为机架，则以该运动链为基础必然会得到包括高副在内的各种新机构。新的机械装置的型综合几乎都是采用适当选择的运动链作为创造型综合的基础。

机构型综合方法：

1）首先选取较简单的运动链，不能满足要求时再选结构较复杂的运动链。

2）将运动链中的一个构件固定为机架，给出与运动链自由度数相等的主动件即可得到一个全转动副机构。

3）由于转动副与移动副的约束数相等，因此转动副可以直接变换为移动副（移动副用符号T表示）。

4）由于一个高副与含两个转动副的构件具有相同的约束条件，因此包含两端运动副在内的一个二元连杆可用高副代替（二元连杆变换出的高副用符号HS表示）。

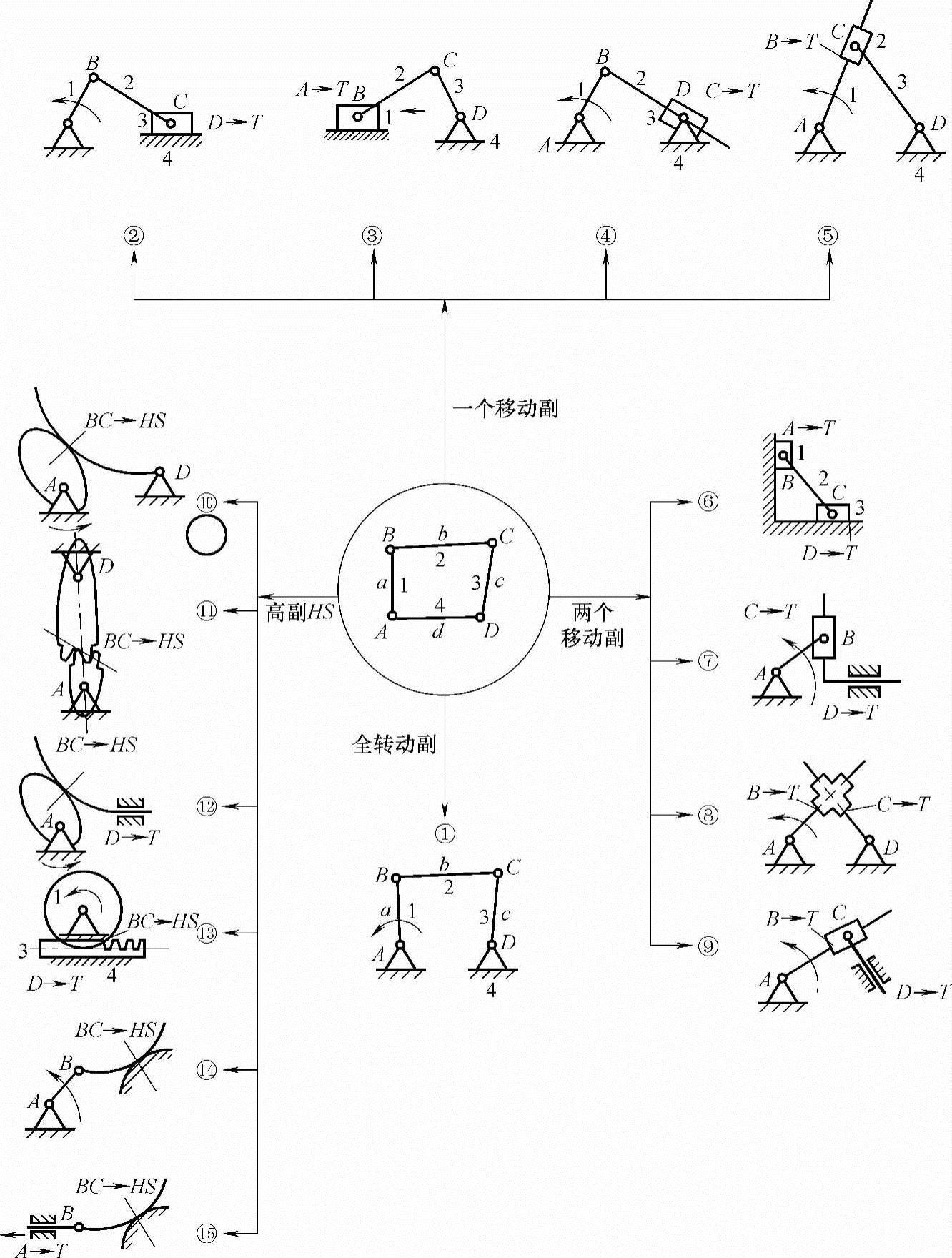
图5-3所示为由F=1的F1A运动链按以上方法变换出的一些机构。若均以构件4为机架，构件1为主动件时，①为全转动副机构，②～⑤为分别选择不同的转动副变换为移动副时的单移动副机构；⑥～⑨分别为选择两个转动副变换为移动副时得到的双移动副机构；⑩～(15)为选择不同的二元连杆为高副及某一转动副再进行移动副变换所得到的机构。理论上讲最简单的F1A类运动链至少可以变换出17种不同的机构。如果再考虑更换机架、更换主动件以及取不同的构件尺寸得到的机构还会更多。

如图5-3所示，(11)为AD固定的两定轴转动的齿轮，若改为固定①中的AB为机架，则原机架AD绕A转动，CD与AD啮合又随AD转动，得到一周转齿轮传动。

(www.xing528.com)

图5-3 F1A运动链机构变换图

如果将图5-3中①的全铰链四杆机构进行尺度变换，当选择不同的构件尺寸比例时可得到运动性质不同的机构。如图5-4a所示，AB整周转动，CD在ψ范围内来回摇摆，称为曲柄摇杆机构；如图5-4b所示，AB与CD均整周转动称为双曲柄机构；如图5-4a中CD固定为机架，取AB为主动件，则AD、BC均摇动，称为双摇杆机构，如图5-4c所示，该机构是以非连架杆为主动件的机构。

如果将图5-3中的⑤表示在图5-5a中，AB的尺寸为a，机架尺寸为d，此时d＞a，当AB整周转动时，作为滑块2的导路的导杆3往复摆动，该机构称为曲柄摆动导杆机构（或称摆动导杆机构）；若取a＞d，则导杆3将整周转动，称为转动导杆机构，如图5-5b所示。

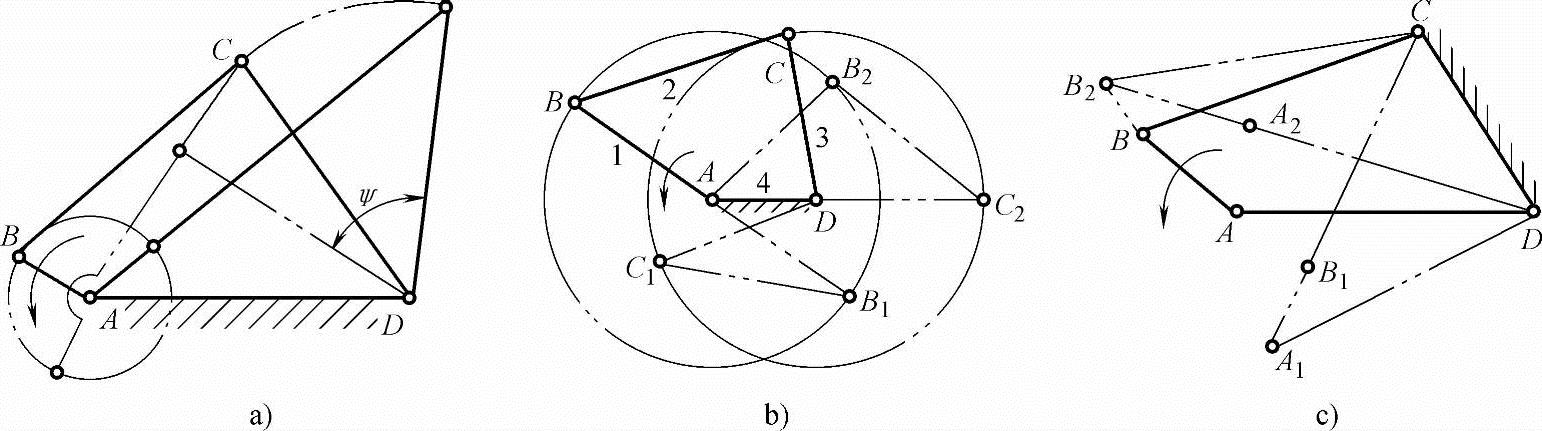
图5-4 铰链四杆机构

a）曲柄摇杆机构 b）双曲柄机构 c）双摇杆机构

由以上分析可见，用运动链变换机构时，应用运动副变换、机架变换、主动件变更及调整各杆尺寸比例，将会得到很多运动性能不同的机构。随着运动链构件数增多，能变换出的机构也会相应增加。