全移动副机构的运动分析

作一般平面运动的二杆组以上的机构均为高级机构，因为其位置方程是一个多元非线性方程组，不能由代数式直接求解而采用计算机迭代计算其近似值。下面对全移动副机构进行运动分析，检验其是否符合这一规律。

1.一杆组机构的运动分析

如图4-20所示，构件1为主动件。已知主动件的位移、速度、加速度：s₁，s₁′=υ₁，s₂″=a₁。

以三个移动副导路相交而构成的三角形OCB建立机构的计算模型。得矢量方程：

s₁=s₃+s₂

OB=OC+CB

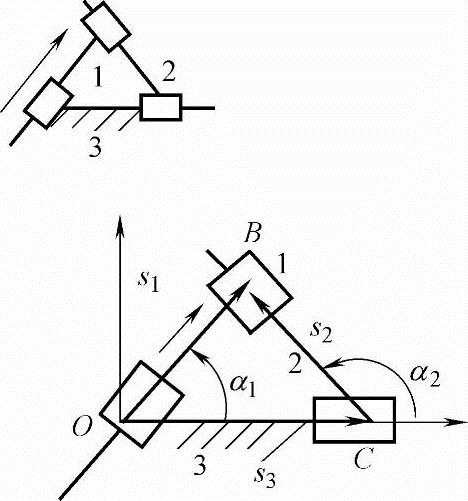
图4-20 1杆组机构运动 分析模型

将矢量方程写成坐标方程：

s₁cosα₁=s₃+s₂cosα₂

（4-14）

s₁sinα₁=s₂sinα₂

整理得

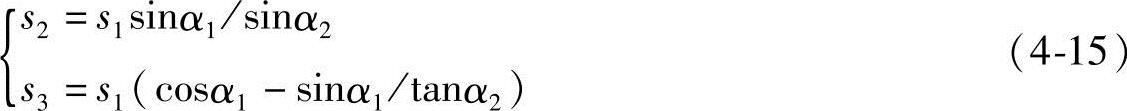
对t求导得速度方程：

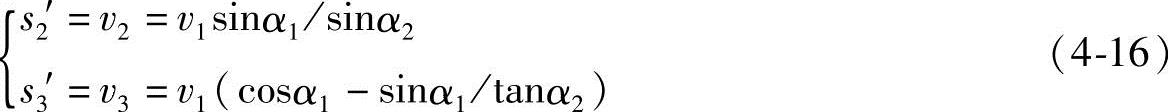
再对t求导得加速度方程：

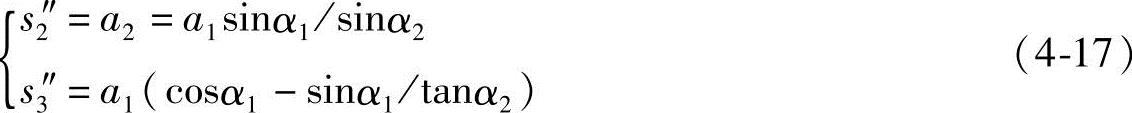
2.二杆组单自由度机构的运动分析

如图4-21a所示，机构的自由度F=2n-p=6-5=1。构件1为主动件且已知为s₁、s₁′=υ₁、s₁″=a₁。

由于机构作平动故所有构件间的夹角不变且为常值。为简化运动分析，按各构件导路相交所构成的图形建立机构计算模型，如图4-21c所示以3个构件1、2、3的固定导路相交的直线KAE为x轴建立坐标系。各构件导路位置角α_i（i=1，2，3，4，5）均为已知且为常量，其方向按逆时针度量。

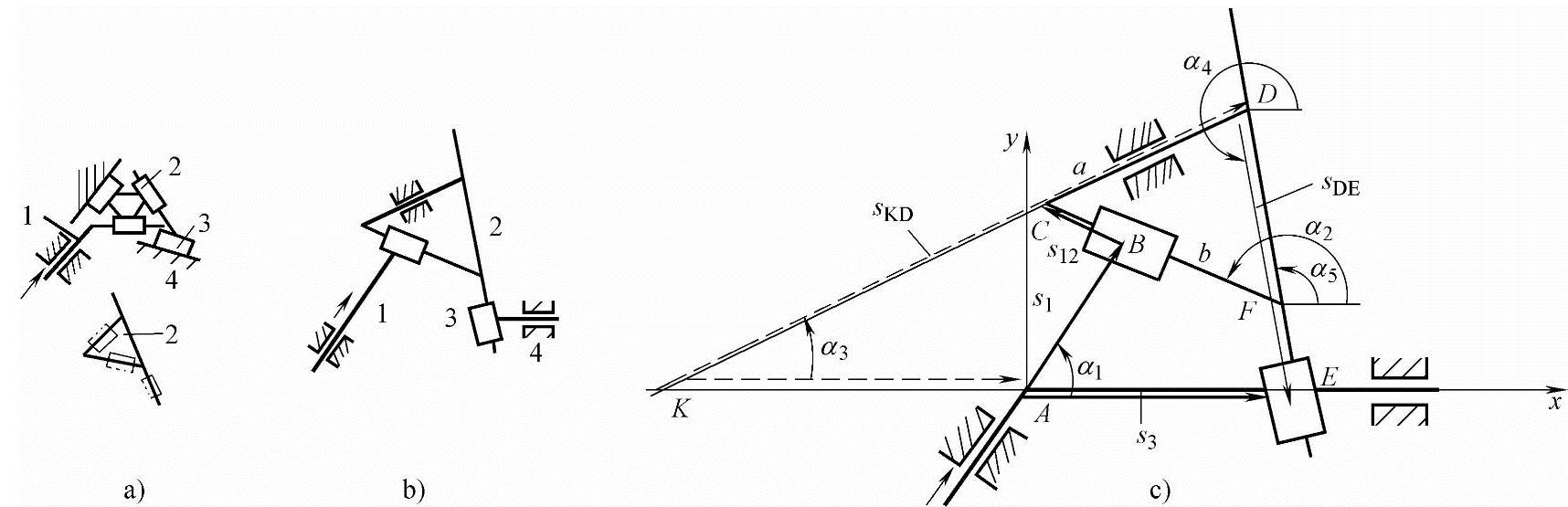
图4-21 二杆组单自由度机构的运动分析

a）二杆组机构 b）机构模型 c）机构分析模型

按封闭回路ABCDEA和KDEAK写出矢量方程：

AB+BC+CD+DE=AE

KD+DE=KA+AE

按矢量方程得到如下坐标方程：

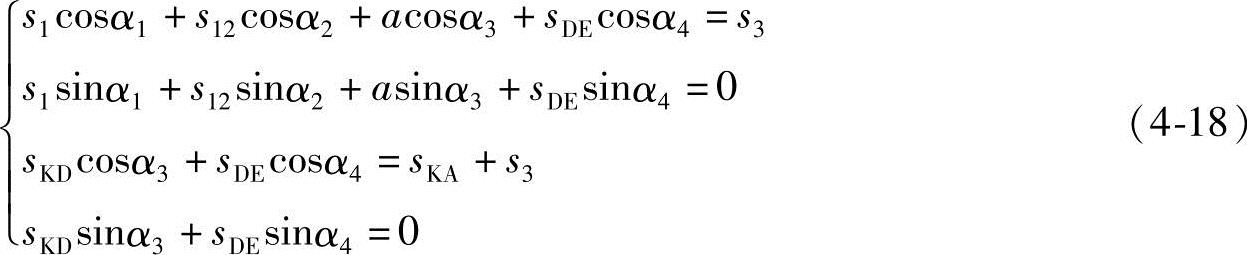(www.xing528.com)

式中，s₁₂、sDE、sKD分别是点B和C、D和E、K和D间的可变距离；s₃为构件3的位移，4个可变位移参数均为待求量；a、s_KA分别为三元连杆和机架的结构尺寸。由于位置角为常数，故上式是一个四元线性方程组。其矩阵为

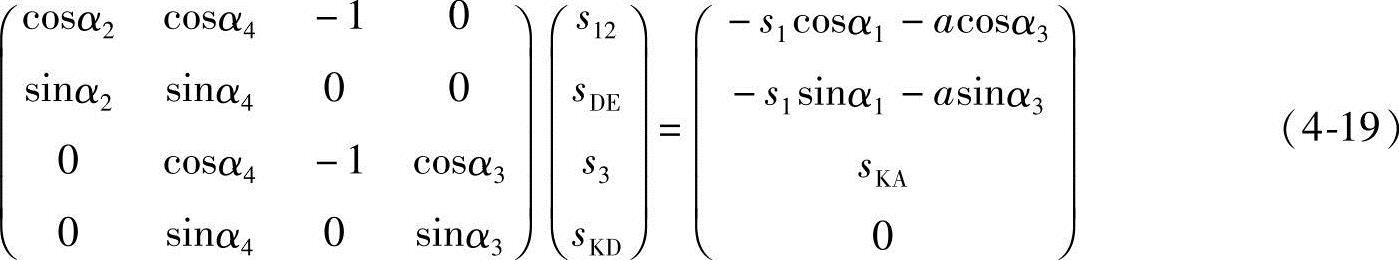
上式对时间t求导可得其速度、加速度方程。

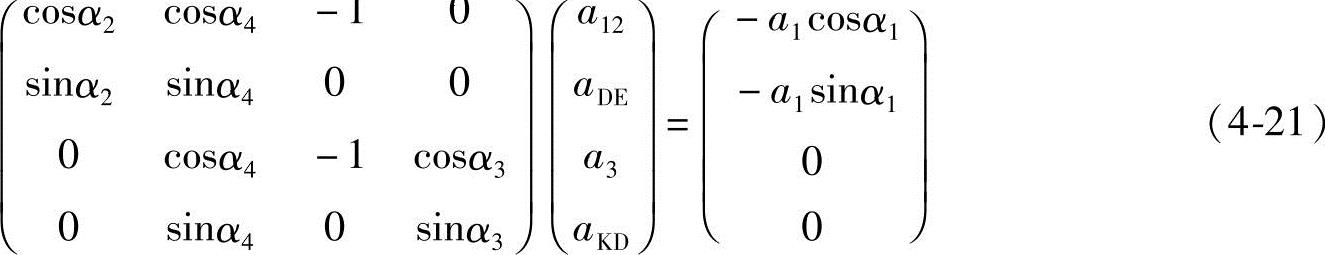
3.二杆组两自由度机构的运动分析方法

如图4-22a所示，机构的自由度为F=2n-p=8-6=2。构件1、4为主动件且已知s₁、s₁′=υ₁、s₁″=a₁，s₄、s₄′=υ₄、s₄″=a₄。三个固定移动导路线交于点A、E、G，以AE为x轴建立坐标系。

将三元连杆2变换为由3个移动副导路构成的三角形构建机构模型，但其大小及方位将不发生变化，即三角形的边长a、b、c和方位角为已知且均不变。

图4-22b中，AB、KG分别为s₁、s₄。改变s₁、s₄时，两主动件推动三元连杆2平动并带动构件3沿其机架导路移动。此时两主动件上的点B、K分别在CF、CD导路上移动。

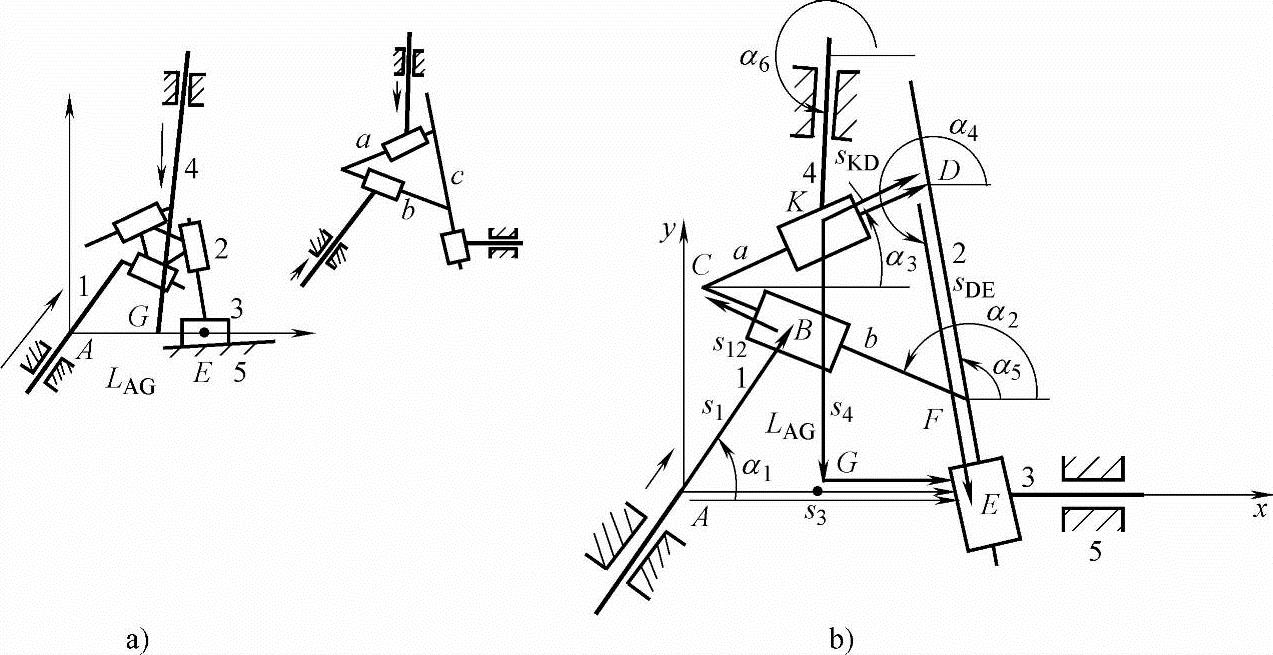
图4-22 二杆组两自由度机构的运动分析

a）二杆组两自由度机构 b）机构运动分析模型

运动分析时按ABCDEA和KGEDK两个回路建立矢量方程：

AB+BC+CD+DE=AE

（4-22）

KG+GE=KD+DE

其坐标方程：

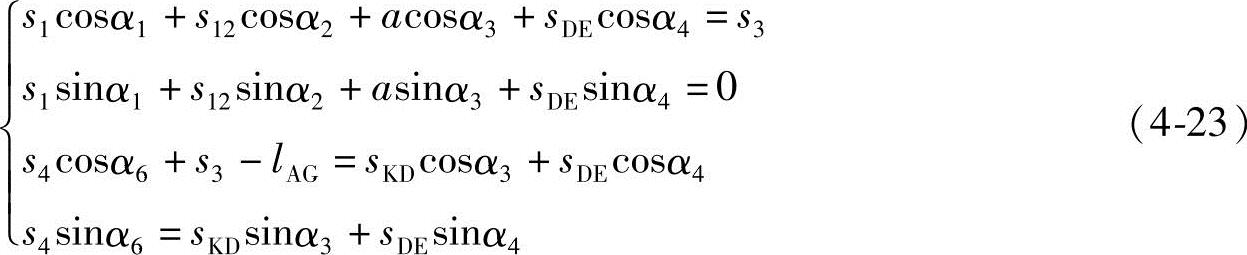
式中，s₁、s₄为给定的已知值，s₁₂、s_KD、s_DE、s3为待求的可变值。由于各矢量的方位角为常量，故该位移方程是待求量的线性方程组。同理可求得其速度、加速度方程。此处不再累述。

4.三杆组机构的运动分析

图4-23a所示为由3个三元连杆2、3、4及主动件1和机架5构成的五杆全移动副机构。

其自由度F=2n-p=8-7=1。若拆去机架和主动件得到P4C杆组。图4-23b所示为机构运动分析的封闭矢量图，各几何量如图。若已知主动件的位移、速度、加速度：s₁，s₁′=υ₁，s₂″=a₁。由封闭回路ABCDA、AHGEA、GFDEG可列出机构位置线性方程组：

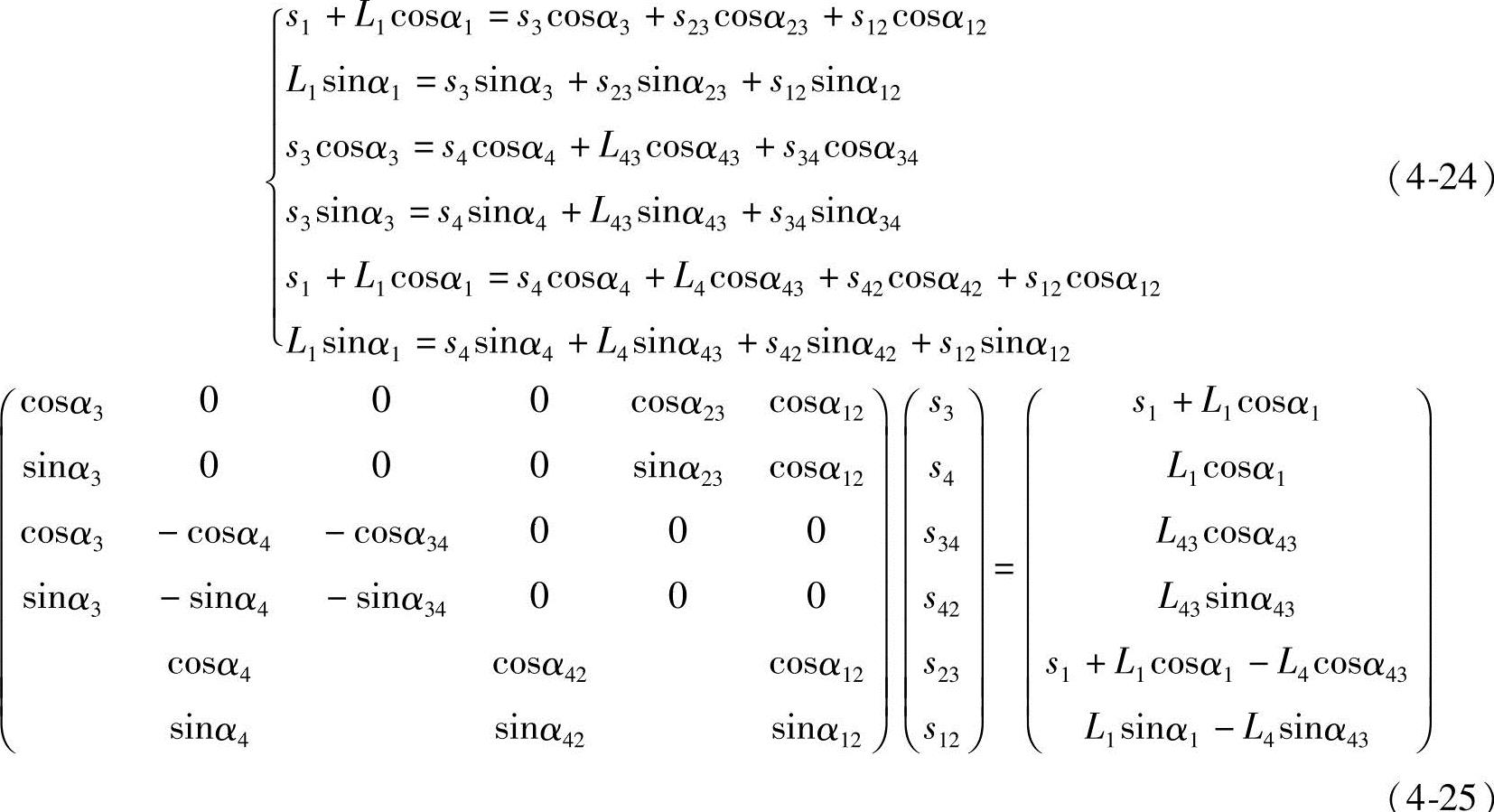
上式对时间t求导，可得到机构的速度、加速度方程。

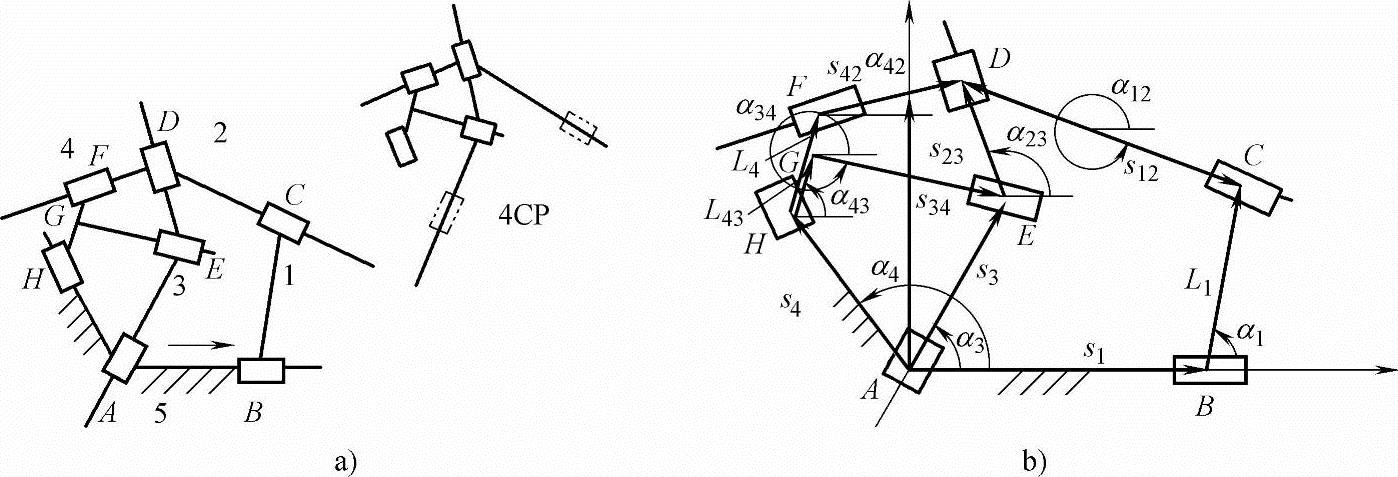
图4-23 三杆组机构的运动分析

a）机构图 b）机构封闭矢量图

综上所述，对于全移动副机构由于各杆位置角是不变的常量，其与一般作平面运动的机构的不同之处是：全移动副机构的运动分析方程式是线性方程，均可得到精确解。因此所有全移动副机构均为低级别机构。