杆组特征值计算公式详述

全移动副机构只能沿平面的两个方向运动，即空间运动加入4个约束。按空间机构自由度公式减去4个公共约束。得到全移动副机构自由度的计算公式：

F=2n-p （4-8）

式中，F为机构自由度，n为机构中的活动构件数，p为移动副的个数。

根据机构组成原理，将机构的机架和主动件拆去得到一个或若干个自由度为零的运动链，这些自由度为零的开式运动链即杆组。由此得到杆组的判断条件为

F=2n-p=0

即

n=p/2 （4-9）

由此得到杆组中构件与移动副间的搭配关系，见表4-8。为区分杆组的简繁程度，以杆组所包含的构件数命名，如P2杆组、P4杆组等。其中符号P表示全移动副杆组。注意，此时的n为杆组构件数。

表4-8 杆组中构件与移动副间的搭配关系

为探求杆组的构型，必须导出杆组中构件数n、移动副数p、外移动副数p_W、环数（L_g）、各元连杆数n_i（i=2、3、4）之间的关系。把分别含有二、三、四个移动副的构件称为二、三、四元连杆。当杆组从机构中拆下时，拆下一个移动副即减少一个环，故杆组的环数为机构运动链的环数减去杆组的外移动副数，即(www.xing528.com)

L_g=p-n+1+p_W （4-10）

由杆组构件数等于各元连杆数之和，得

n=n₂+n₃+n₄ （4-11）

计算杆组的总移动副时，除外移动副外，各元连杆的移动副均重复计算，故得

2p=2n₂+3n₃+4n₄-p_W （4-12）

将式（4-11）、式（4-12）代入式（4-9）得

2n₂+n₃=p_W （4-13）

将式（4-10）、式（4-11）、式（4-13）联立可求解杆组构型

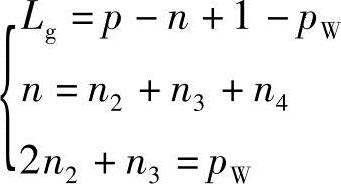
例如分析二杆组（n=2，p=4）构型特征时，由于只有两个构件故杆组不能构成环，即L_g=0。由式（4-10）得p_W=3。由式（4-13）求得n₂=1，n₃=1，n₄=0。以上各参数值即确定了杆组的构型。故把[n₂n₃n₄p_WL_g]的值称为杆组的特征值。如二杆组的特征值[n₂n₃n₄p_WL_g]为11030。