运动链中连杆组合的表示方法

同一特征值的运动链可根据各元连杆的不同连接方式得到不同的构型，这种各元连杆以不同连接方式连接而成的连杆组合的集合称为连杆组合异构体。探求异构体的有效方法仍是拓扑图法。拓扑图法不仅可快速确定各元连杆的连接方式，还可判定构型结构是否合理可行。如图3-2所示，特征值为75012的运动链。它有7个运动副、6个构件、5个二元连杆、1个四元连杆、两个环。由结构图知，四元连杆上的三角形构成刚性结构而不能运动，该运动链实际上是一个四杆运动链，是一个六杆不可行运动链，应废弃。特征值为74202的运动链有两个异构体，即著名的watt型和stephenson型运动链。应用拓扑图可以得到全部运动链的构型。F=1的运动链共有7类20个异构体；F=2的运动链共有7类36个异构体。见图3-3～图3-7及表3-3、表3-4。F=3的运动链共有6类28个异构体，见表3-5。

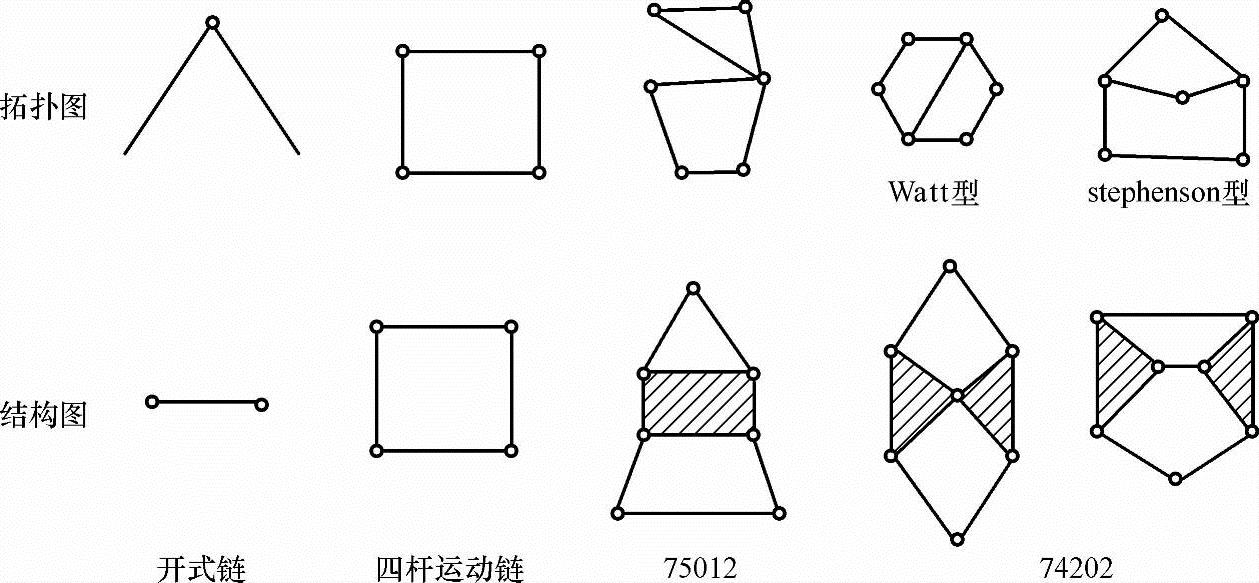
图3-2 几种运动链的构型

表3-3 F=1的闭式运动链数组构型表

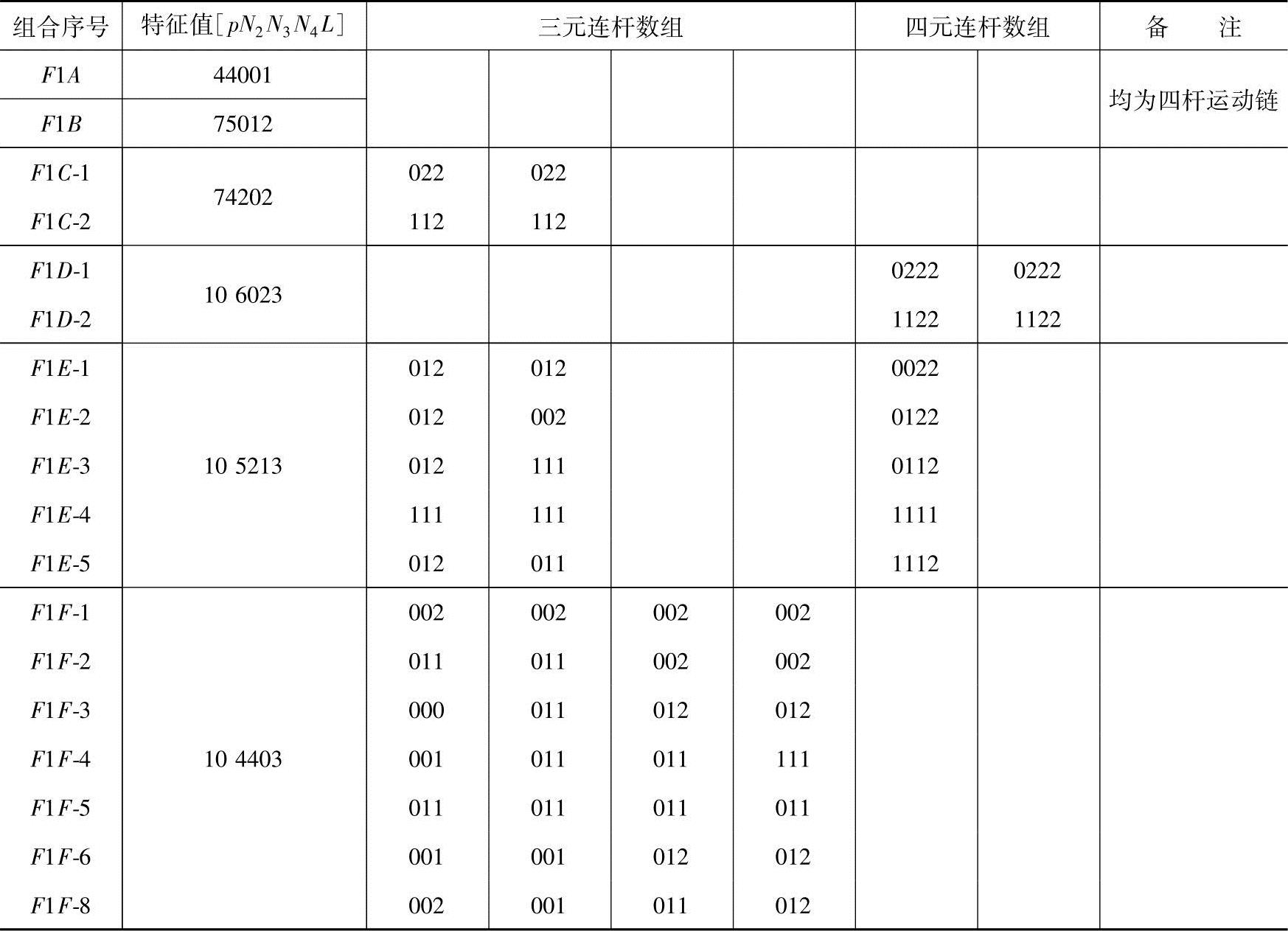
表3-4 F=2的闭式运动链数组构型表

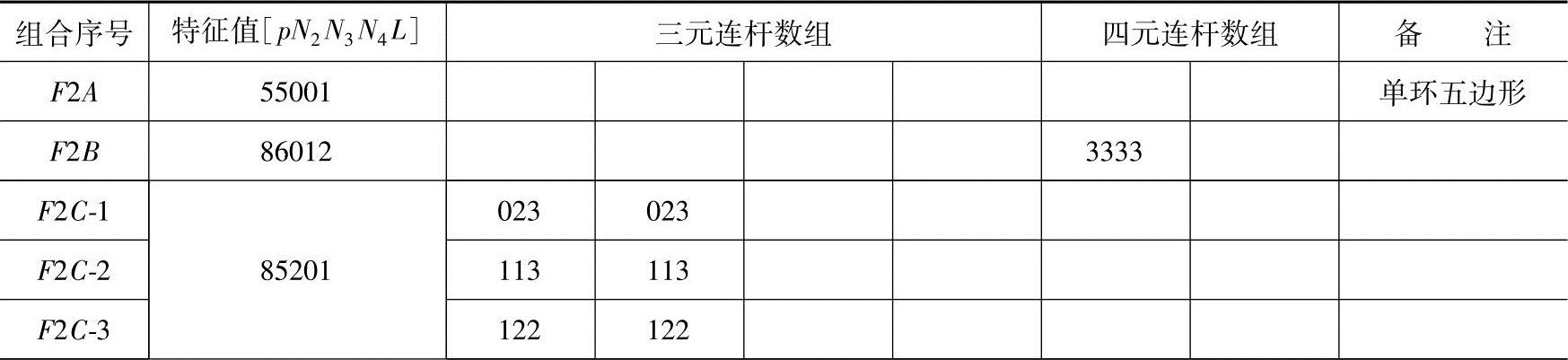
（续）

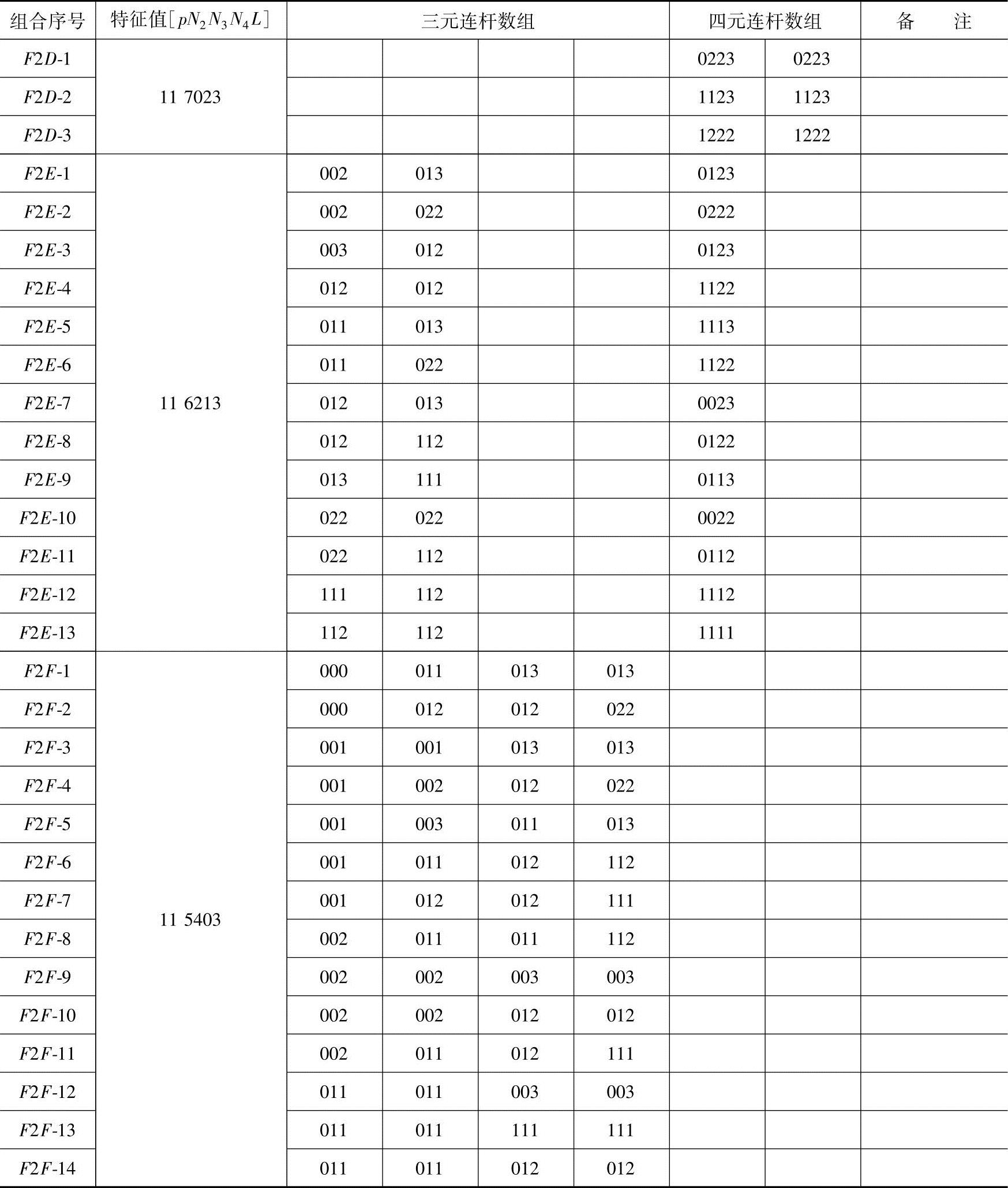
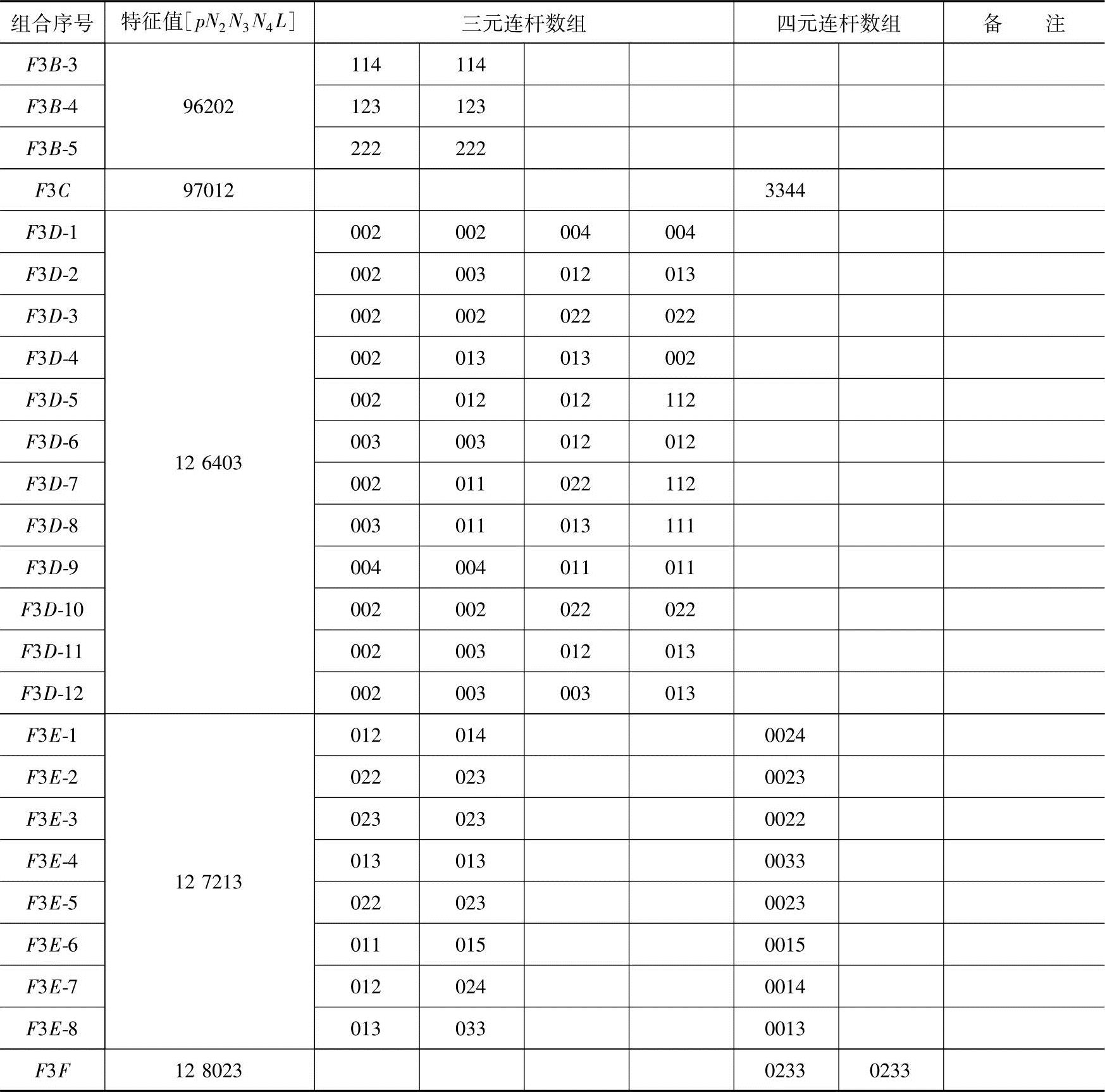
表3-5 F=3闭式运动链数组构型表

(www.xing528.com)

（续）

连杆组合异构体有两种表示方法，即结构图表示法和数组表示法。

为清楚地表示出运动链的结构形式，二元、三元及四元连杆分别用符号N₂、N₃及N₄表示，用数组表示多元连杆与二元连杆的连接方式的规则为：

1）每一数组表示一个多元连杆的连接方式，因此数组的个数与该运动链中多元连杆数相等。

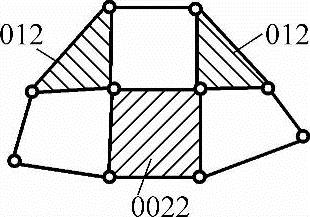
图3-3 F1E-1运动链的数组表示方法

2）数组中数的个数与多元连杆的元数相等。如某三元连杆用三个数组成的数组×××表示，四元连杆用四个数组成的数组××××表示。

3）数组中某数的值表示该副元素上串联的二元连杆的个数；两个多元连杆在该运动副上直接相连时，用数值“0”表示。

如图3-3所示，两个三元连杆与四元连杆直接相连，用“0”表示；其他两个运动副分别连有一个和两个二元连杆，用“12”表示。故两个三元连杆表示为：012、012。四元连杆分别与两个三元连杆直接相连，用“00”表示。另外两个运动副串联两个二元连杆，用“22”表示。故该四元连杆表示为0022。故F1E-1运动链的数组表示为012；012；0022。