运动分析：不同级别机构的特点比较

Ⅲ级、Ⅳ级机构一定为非单环机构。该机构中由某单环封闭回路所建立的坐标方程数少于待求量数而无法求解，因此，必须按各封闭回路分别列出全部坐标方程。由于两个以上方程构成的非线性方程组不能用代数式直接求解，而必须采用数值迭代方法求其近似值，相对Ⅱ级机构其计算难度大大提高。因此，把Ⅲ、Ⅳ级机构称为高级别机构。

如图2-8所示机构是由主动件1、机架6与Ⅳ级杆组BCDEGF所组成的Ⅳ级机构。由回路ABCDEA和ABFGEA可列出四个位移坐标方程：

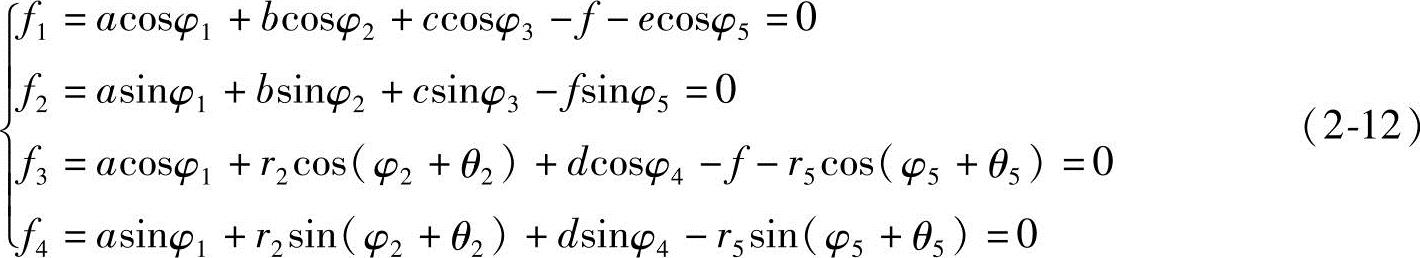
式（2-12）是以φ₂，φ₃，φ₄，φ₅为待求量的非线性方程组。采用Newton-Raphson算法

用式（1-5）来求解。先选定φ_i（0），由式（2-12）求出φ_i（0）处的f_i及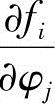（i=1，2，3，4；j=2，3，4，5），按下式求解各迭代增量Δφ₂，Δφ₃，Δφ₄，Δφ₅：

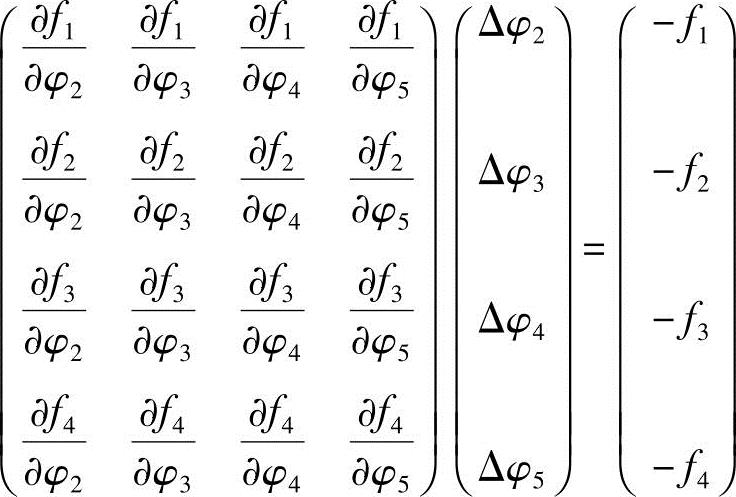
根据式（2-12）求得

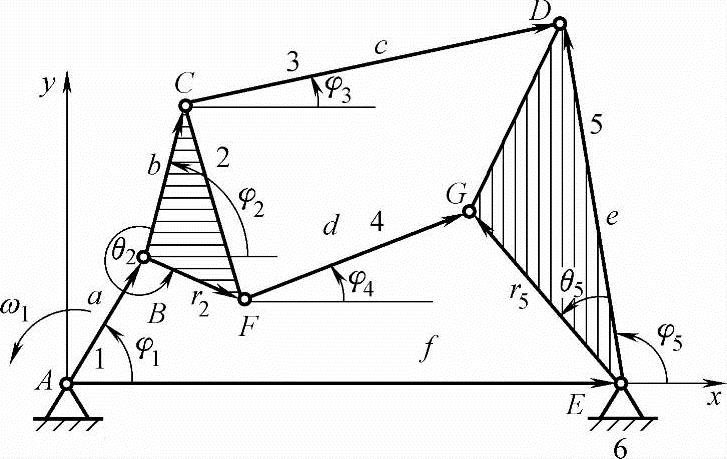
图2-8 Ⅵ级机构运动分析模型

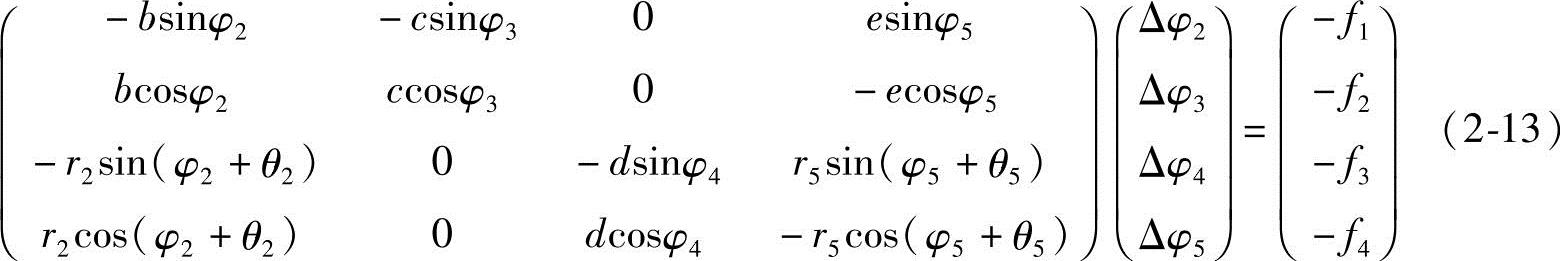
得到迭代增量Δφ₂^（0），Δφ₃^（0），Δφ₄^（0），Δφ₅^（0）和下一次的迭代变量

φj^（1）=φ_j^（0）+Δφ_j^（0） （j=2，3，4，5）

从而可计算出第一次迭代的位移函数f_i（1）（i=1，2，3，4）。如此反复迭代直到第r次，若(www.xing528.com)

f_i^（r）≤ε_i（i=1，2，3，4）则终止计算。其中ε_i为各函数f_i设定的计算精度。

该机构的速度及加速度分析方法与Ⅱ级机构类似，不再累述。

例2-1 Ⅲ级机构运动参数计算。

如图2-9所示，已知a=20mm，b=r₃=50mm，c=40mm，d=30mm，f=70.7mm，θ₃=68°，θ₆=135°，e=10，ω=10rad/s，求主动件φ₁=30°时的s，。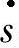

解：根据图2-9所示各矢量，分别按矢量封闭回路ABCDE和EDFG列出位移方程

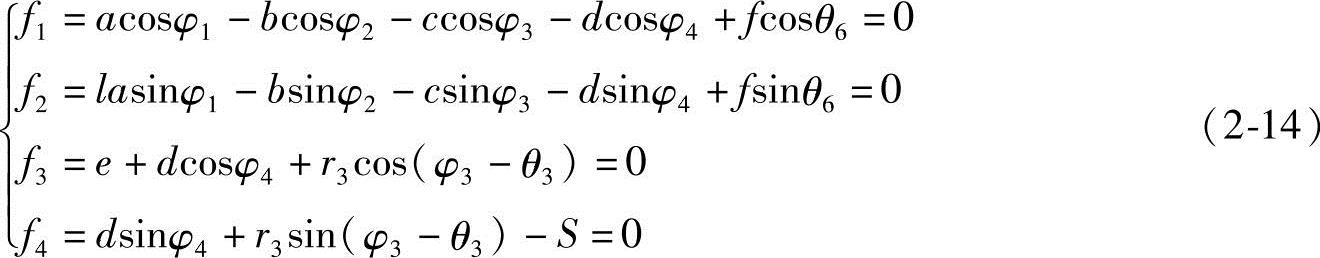
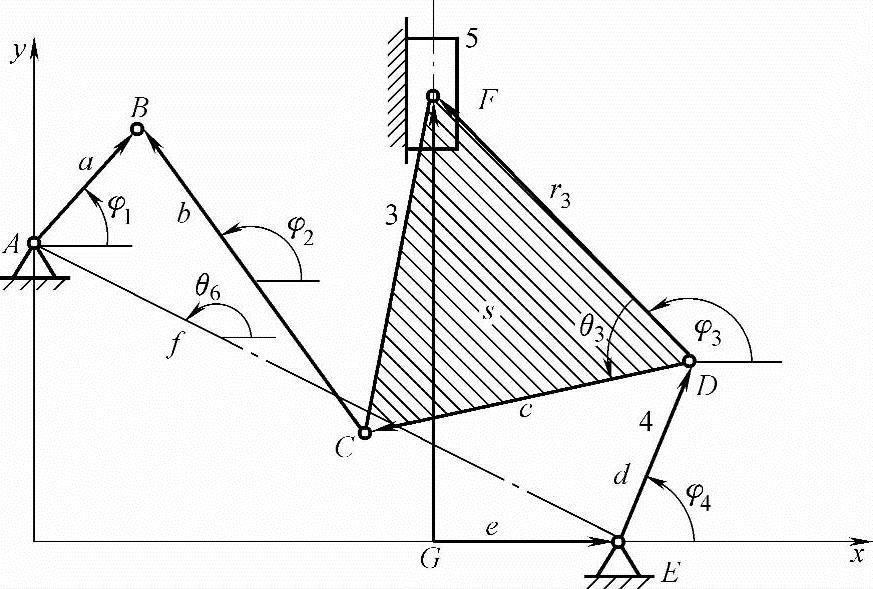
图2-9 Ⅲ级机构运动分析模型

根据Newton-Raphson算法，列出求解未知量增量的矩阵方程

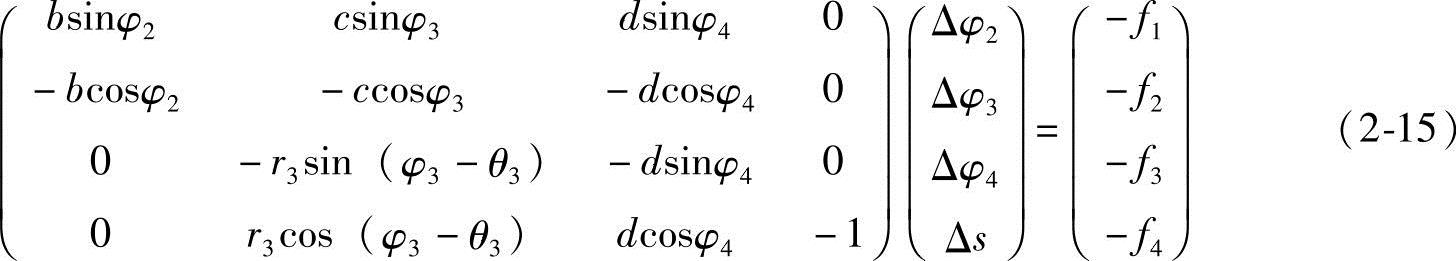
用试凑方法绘制机构，量取各待求量的值作为初值，运用由GAUSS主元消去法构建的Newton-Raphson算法，输入初值后即可求解。

该机构的速度及加速度分析方法与Ⅱ级机构类似，不再累述。