【摘要】：Ⅱ级机构即全由Ⅱ级杆组所组成的机构。如铰链四杆机构、曲柄滑块机构和导杆机构均为Ⅱ级机构。已知机构尺寸，主动件的位置角φ1，其角速度ω1为常数，试分析M点位移、速度、加速度的求解方法。求解程序：首先建立机构的位置方程式，求出给定φ1时的构件2、3的位置角φ2，φ3。表2-2 曲柄滑块机构、导杆机构运动参数计算公式其他Ⅱ级机构的运动分析计算公式列于表2-2。
Ⅱ级机构即全由Ⅱ级杆组所组成的机构。如铰链四杆机构、曲柄滑块机构和导杆机构均为Ⅱ级机构。
图2-7所示为铰链四杆机构。已知机构尺寸，主动件的位置角φ1，其角速度ω1为常数，试分析M点位移、速度、加速度的求解方法。
求解程序：首先建立机构的位置方程式，求出给定φ1时的构件2、3的位置角φ2，φ3。将位置方程分别对时间t求导，得速度方程式和加速度方程式，并求得各构件的角速度ω2，ω3和角加速度ε2，ε3。最后列出M点的位置方程并对t求导即可完成。
由矢量封闭回路ABCD写出矢量方程
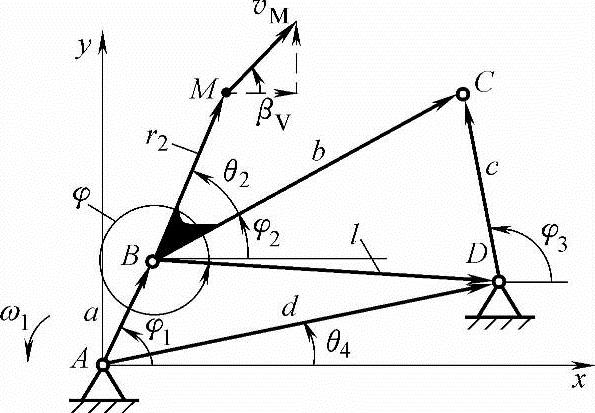
图2-7 铰链四杆机构运动分析模
a+b=c+d
将上述矢量方程写成坐标方程
式（2-3）的待求量为φ2，φ3。由于该方程为φ2，φ3的非线性方程，为方便起见，在
图2-7中加辅助矢量BD，即l，φ。在封闭矢量回路ABD和BCD中得
a+l=d
b=l+c
其坐标方程为
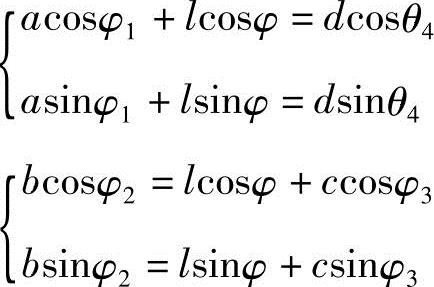
解得
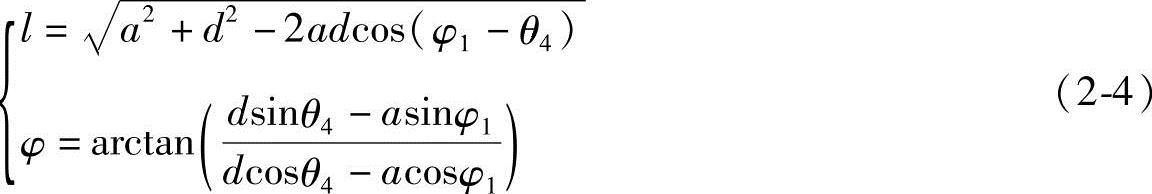(https://www.xing528.com)
及
将式（2-3）对t求导，可求得
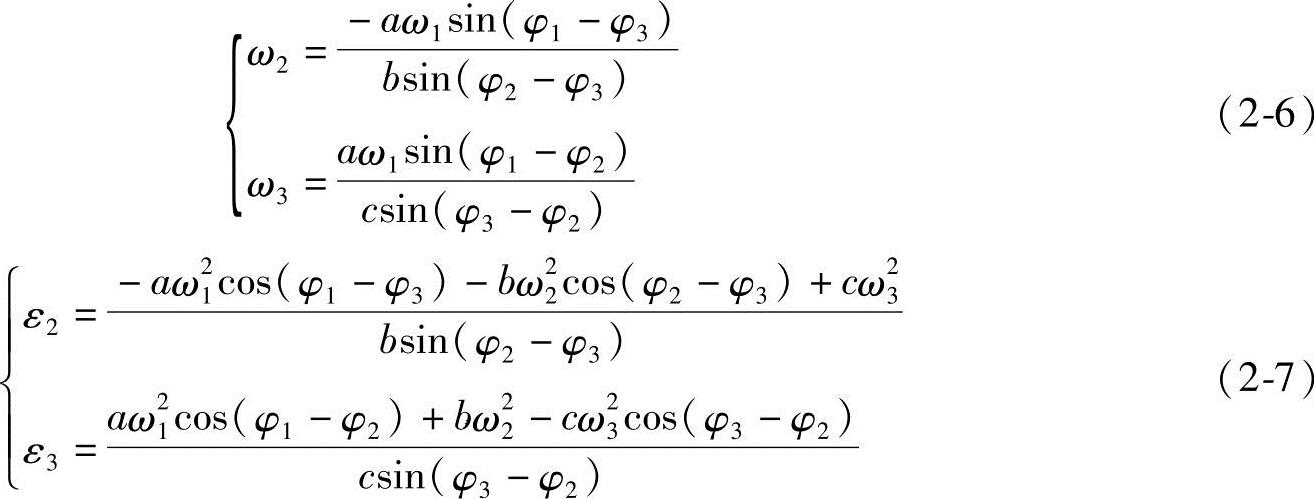
M点的坐标用xM，yM表示，则
式（2-8）对时间t求导得
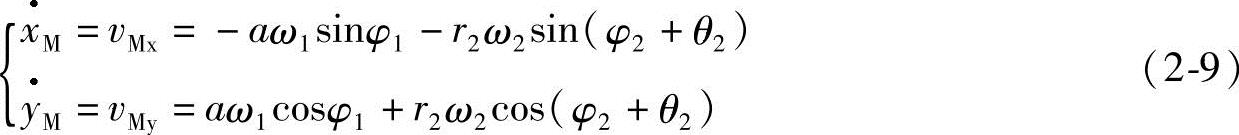
式（2-9）对时间t求导得
若M点的速度大小及方向角用vM和βV表示；M点的加速度大小及方向角用aM，βa表示，则得
其他Ⅱ级机构的运动分析计算公式列于表2-2。
表2-2 曲柄滑块机构、导杆机构运动参数计算公式
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
