机构综合与优化的优化方法介绍

数学规划被引入机构综合之后，提出了机构的最优化设计问题。机构综合的近似方法必然存在结构误差，而这种结构误差是机构参数的函数。如何确定机构的各个结构参数以使结构误差最小，就是一个数学规划问题。如果从机构的具体工作要求出发对机构的结构参数、运动参数和某些动力学参数加上一定的约束，在此条件下如何合理地确定机构的参数（包含结构参数）以使预定追求的目标值误差（包括结构误差及其他性能误差）最小，这就是机构优化问题。

在机构优化问题中，关键之一是建立优化数学模型，其二是优化方法。由于本书的重点不是优化方法，因此仅从实用观点出发介绍优化的一般概念以及实用的两种优化方法。对优化方法的深入研究可参阅有关专著。

优化问题的数学模型包括设计变量、目标函数及约束条件。例如在B×L的长方形地基上要求建一个容积为V₀，长宽高分别为x₁，x₂，x₃的水箱，要求材料消耗最少。这就是一个优化问题。所谓目标函数即设计目标，它是以设计变量为函数的数学表达式。所谓设计变量就是作为目标函数自变量的独立设计参数，如水箱长宽高三个设计参数中只有两个是独立的，另一个必须满足已知水箱容积V₀=x₁x₂x₃的要求，如确定x₁，x₂为设计变量，则x₃=V₀/（x₁x₂）为非独立设计参数，就不能作为设计变量。该数学模型就可以写成如下形式：

目标函数：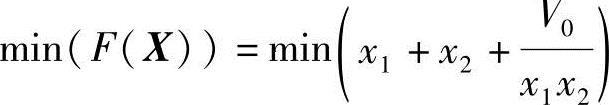

设计变量：X=（x₁x₂）T

目标函数：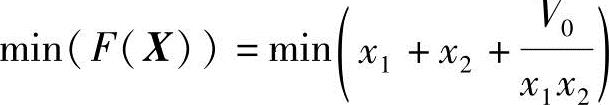

设计变量：X=（x₁x₂）T(www.xing528.com)

约束条件：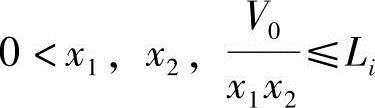

式中，L_i表示x₁、x₂、V₀/（x₁x₂）中人为规定的尺寸上限。可以根据优化方法不断改变x₁，x₂的值，使得目标函数F（X）值最小。这一计算过程是从若干个甚至几十个、几百个方案中找到F（X）值最小的最优方案。可见这一计算过程必须借助于计算机完成。

优化方法尽管是一个近似方法，但一般可以达到工程上要求的足够精度。此法与其他方法相比的一个突出优点是：不但可以实现机构在位置上的预期要求，而且能使机构具有优良的运动性能和动力性能，它是机构综合中对各类设计问题都适用的一种方便的方法。

约束条件：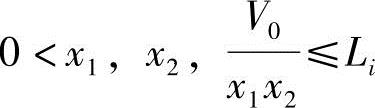

式中，L_i表示x₁、x₂、V₀/（x₁x₂）中人为规定的尺寸上限。可以根据优化方法不断改变x₁，x₂的值，使得目标函数F（X）值最小。这一计算过程是从若干个甚至几十个、几百个方案中找到F（X）值最小的最优方案。可见这一计算过程必须借助于计算机完成。

优化方法尽管是一个近似方法，但一般可以达到工程上要求的足够精度。此法与其他方法相比的一个突出优点是：不但可以实现机构在位置上的预期要求，而且能使机构具有优良的运动性能和动力性能，它是机构综合中对各类设计问题都适用的一种方便的方法。