数值迭代法：解决多元非线性方程的有效方法

在机构分析和综合中常常遇到求解多元非线性方程的问题，而当方程元数增多时，这一求解过程几乎难以建立。此时可采用其级数并用迭代方法近似求解。

对于单变量非线性函数f（x）=0，若当f（x）在x₀处各阶导数均存在时，其在x₀的邻域内的泰勒（Talor）公式为

图1-7 切比雪夫零值公式几何表述

若近似取其线性项，则有

f（x）≈f（x₀）+f′（x₀）（x-x₀） （1-3）

用式（1-3）可以将f（x）关于x的非线性方程化为近似的线性方程。此即非线性方程近似线性化。这一方法将在高级别机构的运动分析中应用。

对于多变量非线性函数f（X）=0，在点X（0）=（x₁（0），x₂（0），…，x_n（0））T处各阶导数均存在时，其在X（0）的邻域内的泰勒公式为

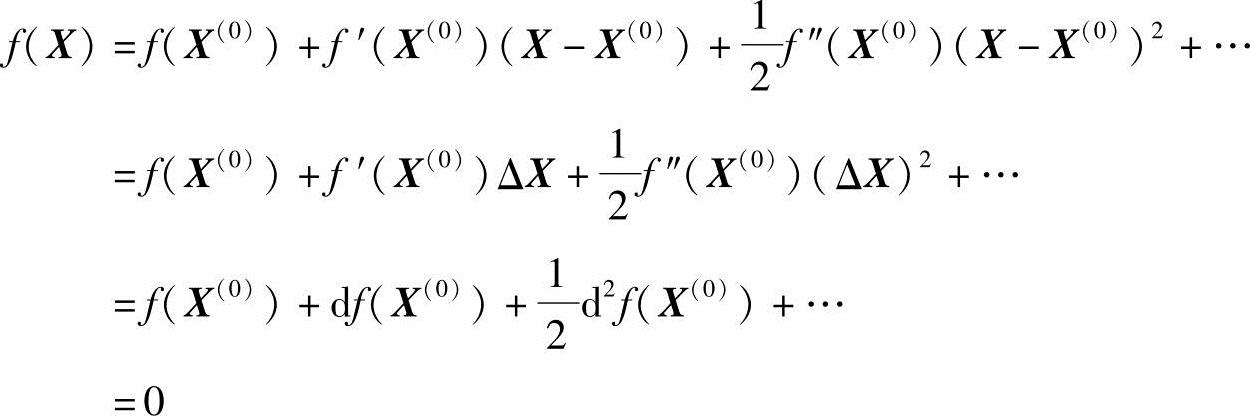
若近似取其线性项，则有

f（X）≈f（X^（0））+df（X^（0））≈0 （1-4）

而

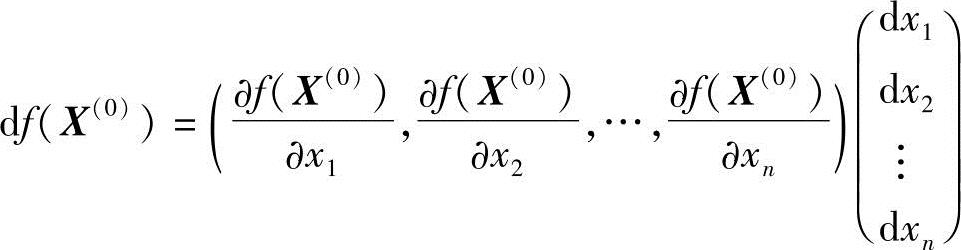(https://www.xing528.com)

于是对任一非线性函数组

f_j（X）=0，j=1～n

有方程

为简化符号，记f_j（X（0））为f_j，且用Δx_i代替dx_i，i=1～n，则有

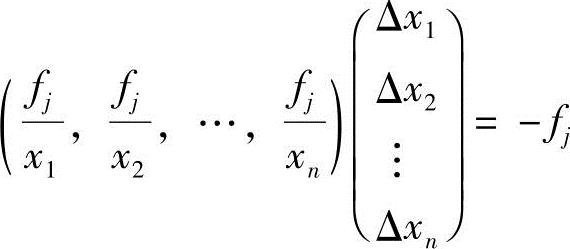
因此对于整个非线性方程组f_j（X）=0（j=1～n），可得

由式（1-5）求出第k次迭代的ΔX（k）后，再由下式求出第k+1次迭代的X^（k+1）

X^（k+1）=X^（k）+ΔX^（k）就可以求出k+1点处的f_j（X^（k+1））的值。如此反复直到k+r次使得

∑|f_j（X^（k+r）+ΔX^（k+r）|≤ε

式中，ε为根据需要所规定的小值。此时的X^（k+r+1）即为所求。

此种逼近求解方法通常称为牛顿-拉普森（Newton-Raphson）算法。