准点解析法：简化准点法机构综合

在用解析法进行机构综合时，若不要求机构运动区域内准确地实现给定的条件，而只要求在域内几个给定位置处符合给定条件，该设计方法称为准点解析法（或称准点法）。所指定的符合预定条件的几个位置称为准点。

例如刚体导引机构综合。如图1-6所示，刚体位置用其上一直线MN表示，给定M点的运动轨迹y=f（x）和MN的转角变化规律φ=φ（x）。设所设计的机构某构件上M′N′的导引规律的对应参数用y′、φ′表示，显然y′、φ′均是机构结构参数r_k的函数。

y=f（x，r_k）

（k=1，2，…，m） （1-1）

φ′=φ（x，r_k）

式中，r_k为机构的结构参数；m为结构参数的个数。一般来说，选定的r_k使y=y′、φ=φ′是不可能的。但可以在指定的几个点位x₁，x₂，…，x_n上，设法选定r_k得到：

f（x_i）=f（x_i，r_k）

（i=1，2，…，n）

φ（x_i）=φ（x_i，r_k）

式中，n为自变量x给定值的个数，所指定的n个位置即n个准点。(www.xing528.com)

上式说明，机构所实现的运动关系只在准点处与预定的运动关系相符，而准点以外，则允许有差异。此即为准点法机构综合。

准点以外y与y′不等，其差值Δy=y-y′，称为机构的结构误差。减小结构误差的可能途径是：

1）增加准点的数目。遗憾的是准点的数目受到所设计的机构的待定结构参数数目的限制，即与准点数n相等的可列方程数应该等于待定的机构结构参数的数目m，式（1-1）才有确定解。此外，准点数目增多求解将变得复杂。

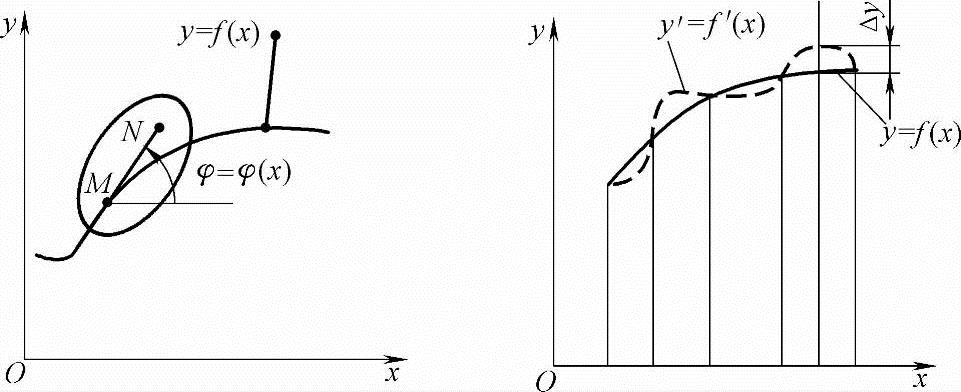
图1-6 刚体MN及其给定M点的运动

2）合理确定准点的分布。研究表明，准点位置分布也会影响结构误差。初步设计时可按切比雪夫零值公式配置准点

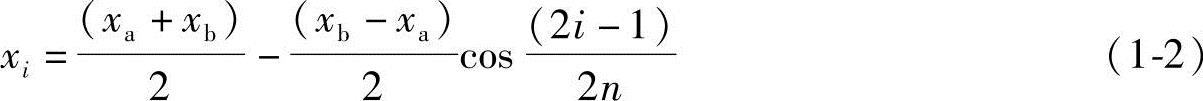
式中，i为准点序号；x_a，x_b为逼近域的下限和上限；n为准点的数目。

该式几何表述如图1-7所示（此时n=4）。