施工管理中的动态规划应用

动态规划方法对于解决多阶段决策过程最优化问题，由于它把原问题分解为一系列形式上很相似的子问题来解决，从而使每个子问题变为比较简单、容易求解的寻优问题，因此是比较有效的。故动态规划方法被广泛地应用于解决工程中的各种实际问题。这里，主要介绍施工企业在施工管理方面应用动态规划方法的几个典型例子，并通过这些例子具体说明建立动态规划模型的方法，以及递推求解的过程。

4.2.1　相邻两个阶段的随机状态变量具有简单的马尔可夫链关系时的动态规划问题

我们知道，在许多问题中各个阶段随机因素之间存在一定的相关关系，例如前一个时段天气状况常常会影响后面一个时段出现各种可能的天气状况的概率分布。在非汛期中相邻两个时段（相邻两个旬或相邻两个月）的河流径流量常常有密切的相关关系。

【例5.20】 某项室外工程，施工期只需1天，要在5天内必须完成。适逢雨季，倘知雨天施工要增加施工费用，大雨施工费800元，小雨为600元，无雨施工费为500元，根据预报第1天的雨情及相应的概率见表5.18。

表5.18　某工程第1天雨情及相应概率情况表

以后各天之间的雨情概率转移矩阵均为：

要求根据天气的情况决策在哪一天进行施工可以使施工费用最省。

解：现以一天为一个阶段，选择最优决策。引用以下符号：

fi（sij）——第i天遇到j种天气sij时的施工费用。

f*i（sij）——第i天遇到sij天气时采用最优决策时的施工费用。——第i+1阶段遇到R种天气时采用最优决策时的施工费。

PjR——第i天发生第j种天气条件下第i+1天发生第R种天气的条件概率，可由概率转移矩阵得到。

问题的递推公式为：

按逆向递推计算如下：

（1）第五天

到达第五天时，无论出现什么天气均应施工，否则不能按要求完成任务。故

（2）第四天（见表5.19）

表5.19　第四天天气情况决策计算表

（3）第三天（见表5.20）

表5.20　第三天天气情况决策计算表

（4）第二天（见表5.21）

表5.21　第二天天气情况决策计算表

（5）第一天（见表5.22）

表5.22　第一天天气情况决策计算表

根据第五天至第一天的计算可以得到在各种不同的天气情况下最优的施工安排为：

第一、第二、第三天遇大雨和小雨时均不施工，只有无雨时才施工；

第四天遇大雨时不施工，遇小雨或无雨时均施工；

第五天无论遇到什么天气都要施工。

由以上可以看出，对于具有随机性因素的动态规划所得到的最优策略是具有一定的冒险性的。例如在上例中，若第一、第二、第三天都遇到小雨，而第四、第五天遇到了大雨，按最优策略在第一、第二、第三、第四天均未施工，到第五天时冒大雨进行施工，这时施工费用为800元。这种情况倒不如在第一、第二、第三天时冒小雨施工来得经济。这种情况并不说明这种决策方法是错误的，而是由于未来的天气状态变化过程我们不能确切地知道，所得到的最优策略是根据资料推算可能取得最大效益的一种最好的估计。究竟实际情况是否真会按这种最好的估计而出现，当然不能十分肯定，因此是有一定的冒险性的。

从上例可以看到，应用动态规划的方法不像线性规划那样，必须要求约束条件和目标函数有线性关系。这是动态规划应用广泛、更能反映实际情况的重要原因。(www.xing528.com)

4.2.2　资源分配问题

资源分配问题，是指如何把有限的资源（资金、设备、原材料、人力等）分配给若干使用者，使其发挥最大的效用。

众所周知，同样的资源交给不同的使用者，往往产生的经济效益不大一样。因此，合理分配资源是值得研究的。然而，当使用者比较多时，如何找到一个最合理的分配方案，有时也不是很容易的事。

如果把资源分配给1个使用者看作1个“阶段”，那么资源分配这种“静态”问题也可以当作多阶段决策问题，从而用动态规划的方法来解决。

【例5.21】 某集团公司（建筑业）拟将一种新型高效的施工设备5台分配给所属的3个分公司。各分公司得到这种设备可增加盈利的数量如表5.23所列。试求怎样分配这5台设备，才能使总的盈利增加最多。

表5.23　设备分配计划与增加盈利情况表

解：（1）把分配给一、二、三分公司依次看作第1、第2和第3个阶段。

（2）把每阶段所有待分配的设备数看作该阶段的状态变量sk（k=1，2，3）。

（3）决定分配给k公司的设备数为决策变量xk，允许决策集合为：

{xk|0≤xk≤sk，xk∈Z}

（4）状态转移方程：

sk+1=sk-xk

（5）阶段效应dk（sk，xk）为表5.23所列的盈利增加数

（6）最优指标函数值fk（sk）为对状态sk，从第k公司到第三分公司采用最优分配方案增加盈利的值（最大值）

（7）动态规划基本方程是：

下面来解这个动态规划问题。

先考虑对三分公司的分配（k=3）。状态变量s3=0，1，2，3，4，5，相应的允许决策集合依次为：

{0}，{1}，{2}，{3}，{4}，{5}

各种状态下增加盈利的最大值见表5.24（直接摘自表5.23）。

表5.24　各种状态下增加盈利的最大值计算表

再考虑k=2。状态s2是可供二、三分公司分配的设备数，取值集合仍为：

{0，1，2，3，4，5}

决策变量x2为分配给二分公司的设备数。当s2=5时，有：

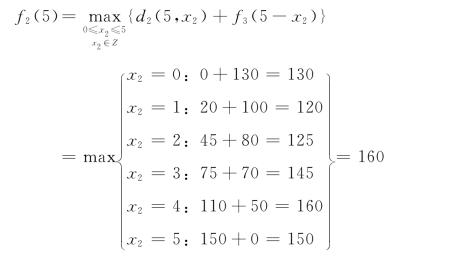
这就是说，若有5台设备供二、三分公司分配，则应分给二分公司4台，留给三分公司1台，这样可使这两个分公司增加的盈利最大（160万元）。

对于s2=0，1，2，3，4，可同样求出f2（s2），以及相应的最优决策x2，计算结果列于表5.25中。

表5.25　状态转移计算表

最后考查k=1。状态变量是待分配的设备数，这里s1=5。现在的问题是研究5台设备如何分配给3个分公司，使增加的总盈利额最大，也就是找原问题的最优解。

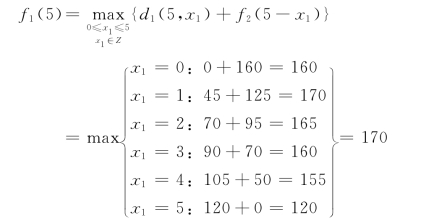
相应地，得x1=1。

这就是说，最优决策是分配给一分公司1台，其余4台留给二、三分公司，查表5.25可知，s2=4时应分配给二分公司3台，三分公司1台。即最优分配方案是给一分公司1台，二分公司3台，三分公司1台，可使3个分公司增加盈利总额达到最大，为170万元。

从解题过程还可以看出，如果计算出f1（4）、f1（3）、…，则容易得到若有4台设备、3台设备等，应如何分配能使总盈利增加最多的问题。