施工管理中最短路的几种问题解析

3.2.1　图的中心、重心与选址问题

图G中有若干个点，其中点v*到距离最远的点的路长是所有点到各自最远点路长的最小者，则称v*为G的中心。可见选址问题实际上就是求一个网络中心（即G的中心）的问题。

一般，设有一个连通网络G=（V，E），G中vi到vj的最短路长记为li，j；G中有n个点，每一个点vj有一个权a（vj）。对每一个顶点vi，令：

那么，满足：

的点vk称为G的重心。

工程中以总运输量最小作为选址标准时，重心就是最好的选点。

求一个网络中心的步骤如下：

第一步：用最短路的标号算法求出网络中每一点到其余各点的最短路长；

第二步：对每一个点vi，找出到距离它最远的点的路长di；

第三步：设，则dl对应的vl即为网络的中心。

【例5.16】 图5.35是某工程施工分布图，是一个边和点都赋权的网络图。7个点代表7个施工部位，点旁括号中的数字表示该处每天的产量（单位：kt），旁边的数字表示相邻两点之间的距离。现在要从v1，v2，…，v7中选一点建砂石料加工厂，问应选哪一点能使各点生产的矿石运往加工厂的总运输量（单位：t·km）最小？

图5.35　某工程施工分布图

解：（1）求G的中心

用双标号法求出G中每一个点到其余各点的最短路长，列成表5.15，并找出表中每一行的最大值，排成右边一列，此列即为各点到离它最远的点的距离。例如到v1最远的距离是（v1，v5）=9.3。

表5.16中{lij}max列的最小者为4.8，它与点v6对应，所以网络的中心即为v6。

（2）重心的确定

若选加工厂建在v1点，则砂石的运输量为：

g（v1）=3×0+2×3+7×5+1×6.3+5×9.3+1×4.5+4×6=122.3

若选加工厂建在v2点，则砂石运输量为：

g（v2）=3×3+2×0+7×2+1×3.3+5×6.3+1×1.5+4×3=71.3

显然选矿厂设在v2比设在v1点好。但v2点是不是运输量最小的选点呢？还不能肯定。

按上述方法，将g（v3），g（v4），…，g（v7）都算出来，取最小者对应的vk，肯定就是符合要求的选矿厂地址。对上述运算可列表进行（见表5.16）。

由表5.16最右边一列最小者为64.5可知，选矿厂应设在v3点。

表5.16　某工程施工点分布最短路计算表

由本例可知，同一个工程中的中心与重心，一般不共点。

3.2.2　设备更新问题

设备的更新是企业管理中十分重要的问题。设备更新的时间N可以根据不同的条件和要求来确定，其中尽量减少设备费用是一个重要的原则。一般，设备使用时间越长，平均到每一年的购置费用l1就越少；另一方面，设备使用时间越长，维修保养费用、能源消耗、停工损失以及效率降低带来的损失都要增加，即设备维修费用l2增加；卖掉旧设备时，设备越旧越不值钱，即残余价值越小。N～l1，l2的关系曲线见图5.36。

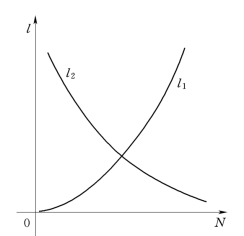
图5.36　N～l1、l2关系曲线图

在制定设备更新计划时，设备费用要考虑购置费、设备维修费及残余价值L。

【例5.17】 某公司购买一台施工用的专用设备，现在单价是每台200万元，两年后预计将提价到250万元。该设备的年维修费和残余价值如表5.17所列。试制定一个总设备费用最少的5年设备更新计划。

表5.17　设备年维修费和残值汇总表

解：可供选择的方案很多。例如每年年初购买一台新的设备，购置费为：

200×2+250×3=1150（万元）

由于设备每年使用的年限为0～1，故5年的总维修费用为：

10×5=50（万元）

5年的报废残余价值共有：

100×5=500（万元）

于是5年的总设备费用为：

1150+50-500=700（万元）

如果采取在第一、第三、第五年各购买一台的方案，则购置费为：(www.xing528.com)

200+250+250=700（万元）

总维修费用：

10+50+10+50+10=130（万元）

报废残余价值共：

75+75+100=250（万元）

于是5年的总设备费用为：

700+130-250=580（万元）

显然，第二个方案比第一个方案设备费用少得多。

现将此问题作最短路问题来研究。

用节点i代表第i年的开头，节点6代表第五年末。由每一个节点向以后各节点作箭线，箭线旁边的数字表示购买一台设备从一个节点使用到另一个节点以后报废，所需的设备费用如图5.37所示。例如：

代表第一年开头购买一台设备，用到第二年底（第三年初）应支付的设备费用：

200+（10+50）-75=185

这样，问题就变成了在图5.37中求节点①到节点⑥的最短路问题。这里的权是支付的设备费用。

用标号算法求出节点①到节点⑥的最短路，如图5.37所示。

由图5.37得出，最短路是（见图中的双箭线）：

图5.37　设备更新计算图

①→②→④→⑥

即第一年初购买一台设备，用一年；第二年初购买一台用两年；第四年初购买一台用到第五年底。这样总设备费用最少，为530万元。

施工设备是施工企业从事生产经营必备的固定资产。为了长期维持设备的既定生产能力，一方面要适时进行设备更新，另一方面，设备更新方案选择的标准为总设备费用最小。

3.2.3　施工现场平面规划的最优化方法问题

施工现场临时性生产设施一般都是沿现场道路网布置，其目的是为了保证施工物质运送方便，以利于施工，同时使其总的运输量达到最小。为了满足施工现场中各施工点的照明、动力和施工用水的需要，开工前首先要在各施工点设置灯具、闸刀或水龙头，并铺设供水供电线路。这些都是施工现场平面规划中的具体内容，那么，如何从安装灯具、闸刀或水龙头的点上设计出理论上最优的供水、供电线路网呢？这要由施工现场的道路的形状而定。对于线状或开口树状的道路来说，如前面所言，临时供水、供电线路沿道路两旁铺设，是不存在选优的问题。而对有闭回路的道路网布置的情况，或者是虽然是无闭回路的道路网络布置，但是牵涉到某个施工功能点（如钢筋加工厂等）的设选，则有选优的条件。选优的方法是归邻法，下面通过具体实例说明该法的具体应用。

3.2.3.1　无闭回路的道路网络布置

【例5.18】 某施工工地需要选定一个钢筋加工厂（车间）的位置，现场道路布置和各施工点及其对钢筋的需用量Qi、还有施工点之间的距离wij如图5.38所示。试确定该施工工地钢筋加工车间的最优位置。

图5.38　施工点分布图

解：这类问题的优选，从内容上看也是属于选址问题。由其所研究问题的特殊性，选优方法工程中一般用所谓的归邻法。其步骤如下：

第一步：计算各施工点总需用量的一半，即。

第二步：归邻计算：将的各施工点需求量并入相邻点的需求量中，但是该点不再加以考虑。一个工程问题一般要经过多次反复归邻计算后才能寻求到所求答案。

表明该施工工地的钢筋加工厂应选在C、G的道路旁，且距施工点C的距离为2.667km。如图5.39所示。

图5.39　某施工现场网络图

3.2.3.2　有闭回路的道路网络布置

【例5.19】 试对图5.40所示的某施工现场网络进行混凝土拌和站位置的选择。图中A、C、E、F、H、J、K为施工点（部位），各点旁边的数据为其相应对混凝土的需用量。其中，B、D、G、I为道路的交叉点，点之间的数据为各段道路的长度（km）。

解：设TD为最佳选址的总运输量，TDi为第i个选址点运往各点的总运输量，先将各分支点用归邻法归邻，使原布置网络为一有回路的网络（见图5.41），然后用如下模型确定最佳选址。

图5.40　某施工现场网络图

由图5.41有：TDB=∑Qiwij={2×1+2×3+4×7+10×6+3×8}×103=120×103（m3-km），意即在B处设站。同理有：TDC=132×103，TDE=121×103，TDG=53×103，TDH=63×103，TDD=101×103，TDF=73×103，TDI=46×103。

图5.41　归邻计算图

可见，。

表明，本工程混凝土拌和站应设在Ⅰ处为最经济。