线性规划模型的求解方法及其应用

线性规划模型的求解，工程应用中有很多成熟的方法，其中主要的有单纯形法、人工变量法、逆矩阵形式的单纯法等。对于简单问题，可以直接用图解法或单纯法的表算法即可求解。对于较复杂的问题（例如决策变量、约束方程较多时），可借助电算来完成求解。

2.2.1　图解法

2.2.1.1　线性规划的基本原理

简单的线性规划问题，可用图解法来求最优解，但此法应用范围只限于含两个变量的问题。其目标函数为：

式中：a、b为已知实数。

所谓求目标函数的极值，就是求一点（x，y），称为极值点，使得Z之对应值为最大或最小。

线性规划的约束条件用作图法来表示，就可构成一个多面凸集。

如图5.28（a）中的三个图均具有凸集特征，而图（b）中的两个图就不是凸集。因为在这两个形体中至少存在两点，在连接它们的线段上不是每一个点都在这类形体之中。

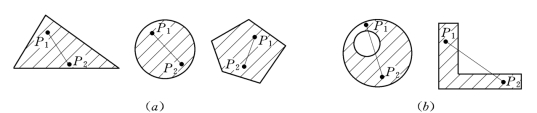
图5.28　凸集形体图举例

在多面凸集内，满足非负约束条件的任何一个点（x，y），称为可行解（feasible solution）。在变量空间中所有可能出现的顶点或极点（Verten），也就是使多于约束方程式个数的变量等于零，由联立约束方程式得到的解称为基本解。凡满足非负条件的基本解称基本可行解。目标函数为最优的可行解称为最优解。目标函数为最优的基本可行解称为最优基本解。下面阐述线性规划的三个基本原理：

1）可行解的集合构成一个凸集，它的每一个极点对应于一个基本可行解。这一原理说明，有意义的解必定包括在可行解的集合之中，而且基本可行解又相当于该集合的顶点。因此，我们着力于研究凸集和它的顶点。

2）若存在可行解，则必存在一个基本可行解。凸集包括了所有可行解，如果我们求得了一个可行解，那么凸集至少存在一个顶点，即至少存在一个基本可行解。

3）若目标函数具有一个有限极小值，则至少有一个最优解是基本可行解。利用图解法解线性规划问题，可沿凸集的边界点上来寻求，这就是数学上常用的迭代方法或搜索法。这实际上就是线性规划问题的单纯形法求解线性规划问题的出发点。

对一般线性规划问题，图解法有三种可能性：无解；有唯一组解；有无穷组解。下面以示例加以说明。

1）无解情况。

【例5.9】 试求Z=x+2y的最小值，且x、y满足x+y≥1。

解：首先画出约束条件x+y≥1的图形（见图5.29）。

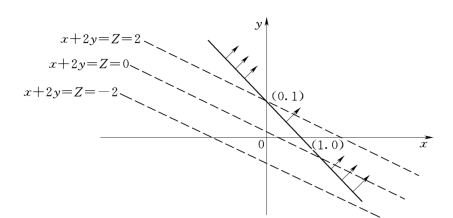
图5.29　无解约束条件图

其次，我们作x+2y=Z之形体，得到一组平行直线，由图形可知，我们找不出Z=x+2y之极值，因为这样的平行线可以无限制地做下去。所以，本线性规划问题无解。

2）有唯一组解情况。

【例5.10】 试求Z=10x+11y的最大值，且（x，y）满足下列约束条件：

3x+4y≤9

5x+2y≤8

x-2y≤1

x≥0，y≥0

解：首先画出约束条件的图形（见图5.30）。

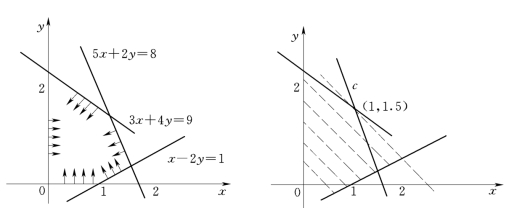
图5.30　有唯一解约束条件图

其次作目标函数Z=10x+11y的图形，得出一组平行直线如图中之虚线。

从图中可以看出，通过顶点c的虚线与x轴之交点是x=2.65，而其他的平行直线与x轴之交点是xi，xi＜2.65，且直线上各线点的数值都相等，因此10x+11y之最大值为26.5，极大点为c点（1，1.5）。

3）有无穷组解情况。

【例5.11】 求Z=2x1-2x2的极大值。

满足约束条件：

-2x1+x2≤2

x1-x2≤1

x1≥0，x2≥0

解：（1）画出约束条件的图形（见图5.31）。

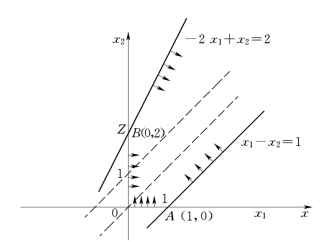
图5.31　有无穷解约束条件图

（2）作目标函数图形。即斜率为的一组平行线（见图5.31）。

由图5.31可看出，目标函数Z=2x1-2x2与第二个约束条件的直线相平行，所以本题有无穷解。

这里，并不是说Z的极大值有无穷多个，而是说x1、x2的取值有无穷多组，即在直线x1-x2=1上任意取一点（x′1，x′2）代入目标函数，都可得到目标函数的极大值，如点A（1，0），则：

Z=2x1-2x2=2

上述例子可以说是纯数学的，现在举几个实际问题的例子，对于实例的处理步骤通常为：

1）根据资料写出目标函数的表达式。

2）列出所有的约束条件。

3）求出约束条件所构成的多面凸集的顶点。

4）求出每个顶点在目标函数上的值。

5）就前一步骤所得到的值，依极大或极小而取舍。

2.2.1.2　工程应用举例

【例5.12】 以例5.8为例说明图解法的具体操作过程。

解：由例5.8中的线性规划数学模型绘制约束条件的图形见图5.32。

图5.32　某施工项目砂石料供应线性规划图解结果

因此得到四个顶点：

A（0，6）、B（1，3）、C（3，1）、D（6，0）

将这些顶点代入目标函数

Z=2x1+1.6x2

Z（0，6）=2（0）+1.6（6）=9.6(www.xing528.com)

Z（1，3）=2（1）+1.6（3）=6.8

Z（3，1）=2（3）+1.6（1）=7.6

Z（6，0）=2（6）+1.6（0）=12.0

上列四个数值中以6.8万元为最小，即得极小值为6.8万元，极小点为（1，3），即在第Ⅰ砂石场装设1部，第Ⅱ砂石场装设3部时，其运转成本费为最低。

2.2.2　单纯形法

美国数学家戴塞（G·B·Dantzig）于1947年首先提出用单纯形法来求解线性规划问题。从图解法中可知，若线性规划问题的最优解存在，必定能在其可行解集合的极点（顶点）中找到。它是从一个边界点开始，通过代数运算转到另一个边界点，使函数值上升（极大化问题）或下降（极小化问题）。这种运算称为迭代。实际上迭代是在凸集的边界点上进行的，最后找到最优解。这就是单纯形法的基本思路。

在求解前，先应将式（5.12）或式（5.13）通过引入m个附加变量后化为如下的标准式：

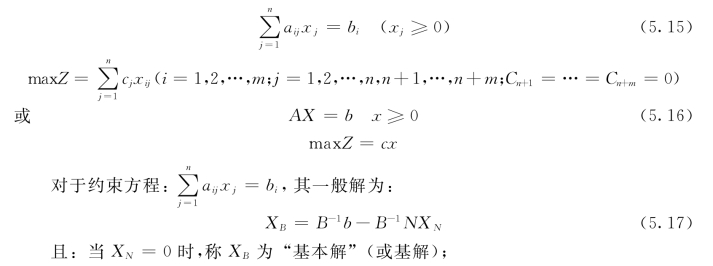
当XN=0且XB≥0时，称XB为“基本可行解”。

而将AX=b中的系数矩阵中m个向量所构成的满秩阵称为“基阵”，与基阵对应的m个变量称为“基本变量”，其余变量称之为“非基变量”（自由变量）。将能满足约束条件的线性规划问题的一个解称之为“可行解”，而所有可行解的集合称之为“可行域”。实际上线性规划问题的基本解与它的可行域的极点是一一对应的。如果最优解存在，必定寓于基本可行解之中。因此寻找最优解的问题就归结为在其可行域的诸极点中去搜索。即：先取一个顶点x（0），代入目标函数Z中[Z（x（0））]，以此为基础再换一个顶点（极点）x（1），并使得Z（x（1））＞Z（x（0））……如此经过有限个步骤即可求得使目标函数达到最大值的极点，即为该问题的最优解。所谓的单纯形法其实质就是上述步骤的一个迭代过程，不过这个迭代过程一般是在表格上进行的。下面介绍表算法的步骤：

（1）两个名词。

1）检验行：指当目标函数Z中基变量系数为零时，所对应行为检验行。如果不为零，可通过初等变换达到这一点。

2）检验数：指检验行中变量Xj所对应的系数σj，称之为Xj的检验数。

（2）表算步骤。

1）找出原始可行基，确定初始基本可行解，建立初始单纯形表（见表5.13）。

2）检查对应于非基变量的检验数σj（适用于求maxZ，AX≤b）：当σj≤0（j=m+1，…，n），表明已得到最优解，停止计算，否则转下一步。在σj＞0中，若有一个σk对应于xk的系数列向量Pk≤0（即对i=1，2，…，m，均有aik≤0），表明无最优解，可停止计算，否则转入下一步。

3）根据max（σj＞0）=σk，确定xk为入基变量，然后根据：

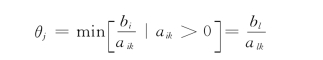
确定Xl为出基变量。

4）在单纯形表中以alk为主元素用高斯消去法进行迭代，即把xk所对应的列向量：

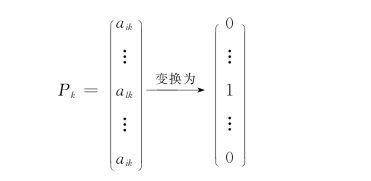
再把xk与xl对换位置后即可得到新的单纯形表，又以此为起点，重复第2）步……一直到得到maxZ为止。

【例5.13】 某地区在同一时期内有若干个项目工程面向社会招标，可供某公司选择的有10项，其中有5项是某水利工程的主体工程，3项是临时工程，还有2项为该工程的生活小区中的工民建工程项目。通过预算，各项工程项目的工程量及预期利润如表5.13所示。试作出正确的投标方案。

表5.13　各项工程的工程量和预期利润统计表

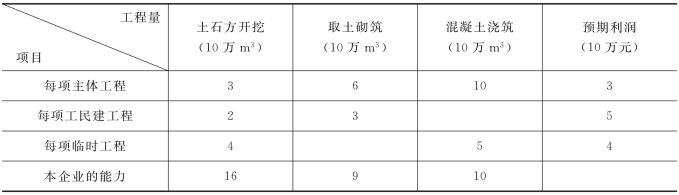
解：线性规划是一种适用范围较广的优化方法，主要解决如何最大限度地发挥有限资源这一类问题。现结合本例来说明其解法的基本原理和大致步骤。

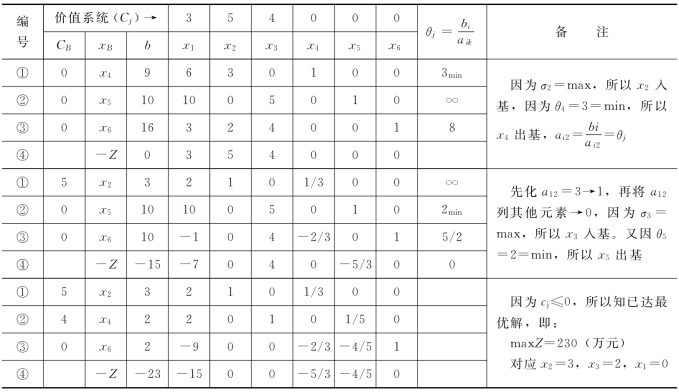
表5.14　单纯法的表算成果

对于本例，将式（5.12）引入附加变量后即得：

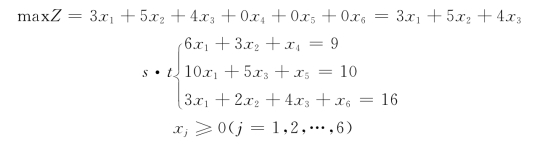
上式即为标准式，在此基础上再列表计算（见表5.14），最后结果表明：

当x2=3，x3=2时，即应选择3项工民建工程项目和2项临时工程作为最佳投标方案，可以满足利润达最大值之目的。

单纯形法的计算步骤可归纳为如下四步：

第一步：首先将原来线性规划问题的数学形式改为标准形式。标准形式的特点是：

1）除了非负条件为不等式外，其余所有约束条件均改为等式。如果原问题约束条件为“≤”形式时，则加入一松弛变量改为等式；如果原问题约束条件为“≥”形式时，则引入剩余变量和人工变量变为等式；如果原问题约束条件为“=”形式时，需引入人工变量使其构成一个基本可行解。

2）约束条件等式右端的常数项必须是非负值，否则需将等式两端同乘以-1。

3）所有变量为非负值。如果有负值变量时，可改写成两个正数变量之差的形式。

4）把目标函数改写成右端为零的等式。对于求极小值问题，可将目标函数乘以-1，把求极小改为求极大来处理。

第二步：选择初始基本可行解。有三种情况：

1）若原问题所有的约束条件全为“≤”形式，则松弛变量可用作初始基本可行解；

2）若原问题所有约束条件全为“≥”形式，则需用人工变量作初始基本可行解；

3）若原问题中的约束条件有“≤”、“=”和“≥”形式时，则需用相应的松弛变量和人工变量作为初始的基本可行解。

第三步：求新的基本可行解：

1）首先确定新的基本可行变量。选择非基本变量是在目标函数式中影响目标函数最大的那个系数的变量，求极大则选负最小值（绝对值最大的负数），求极小则选正最大值。通常称这个变量所在的列为基准列。

2）接着，确定退出变量，以新的基本可行变量来代替。被代替的变量要根据可行性情况决定，就是取约束条件中的各常数项的数值与本行中基准列的正系数的比值最小者。该行称为基准行（基准行与基准列相交元素称基准点）。基准行上的基本变量则退出。

3）经过加减消元，求得一组新的基本可行解。

第四步：确定最优解。求极大值时，必须当非基本变量的目标函数系数项全为非负数时，则最优解已找到；求极小值时，必须当非基本变量的目标函数系数项全为非正数，则最优解便找到。若该条件未满足，则继续按第二步以后的各步骤进行新的迭代计算，直至求得最优解为止。

2.2.3　逆矩阵形式的单纯形法

逆矩阵形式的单纯形法为提高运算速度、节省内存空间提供了理论依据和技术上的支持。

2.2.3.1　公式推导

式（5.13）经标准化处理后为：

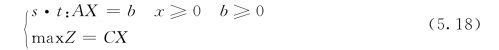
设基阵位于系数矩阵的前m列，即A=（B，N），并将列、行向量分块后有：X=[XB，XN]T，C=[CB，CN]。其中，B=（Pi）（i=1，2，…，m），XB=[x1，x2，…，xm]T，CB=[C1，C2，…，Cm]T，N=[Pm+1，Pm+2，…，Pn]，XN=[Xm+1，Xm+2，…，Xn]T，CN=[Cm+1，Cm+2，…，CN]T。

（2）列表迭代运算（见表5.15）。

表5.15　迭代计算表（逆矩阵形式）

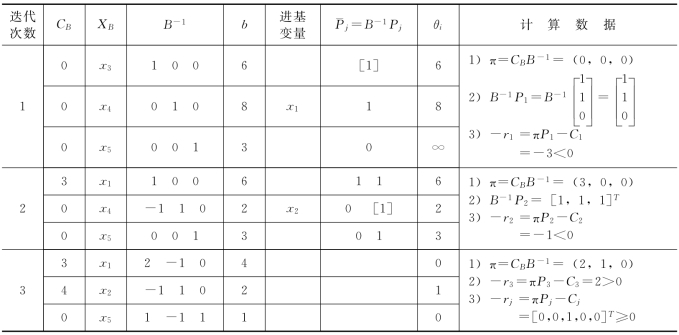
因为-rj≥0，所以知已达最优解，即当x1=4，x2=2时，其目标函数为：maxZ=3x1+4x2=20。