网络图中各工作活动相互关系的综合反映，是网络计划技术的基础。网络图由活动、事项、线路所组成。
（1）活动（或工作） 活动是一项工作或工序，通常是指消耗一定的时间和人力、物力资源才能完成的生产过程或活动过程。此外，由于技术或其他原因引起的某些“停歇”或“等待”，例如混凝土浇筑以后所需的“养护”，也可以作为一项活动或工作来处理，但它只消耗时间，不一定消耗资源。双代号网络图中，活动用标号不同的“矢线”或“箭头”表示（见图5.1），在矢线的上方标明活动的名称（或代号），下方标明完成该项活动所需的时间。矢线的箭头分别表示一项活动的开始和结束，每根矢线的箭头和箭尾均画圆圈，每个圆圈中编有号码。矢线前后两个号码在一起即代表一项工作。单代号网络图是把活动或代号注在圆圈内，矢线只表示前后两项工作之间的顺序关系。现着重介绍双代号网络图，单代号网络图可查阅有关资料。
图5.1 工作代号图
网络图中，除上述活动外，还有一种虚活动，用
箭线表示。虚活动是指作业时间为零的一项活动。它没有活动名称，不消耗资源，也不占用时间，但却起着活动的约束作用，引用虚活动可以把前后的工作或工序连接起来，表示它们之间的逻辑衔接关系，指明活动前进的方向，还可以消除工作或工序间模棱两可、含糊不清的现象。例如，某钢筋混凝土柱基础的施工计划如表5.2所示，其网络图如图5.2所示。
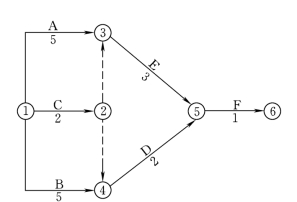
图5.2 钢筋混凝土柱基础网络图
表5.2 某钢筋混凝土柱基础施工计划表
由上例可见，网络图是由
实、虚工作，节点ⓘ（事项）及线路（例如①→②→③→⑤→⑥）所表示的一项工程的计划，反映施工顺序和工作之间相互关系的图形。
（2）事项（或事件） 事项是指某一项活动的开始或结束，一般用圆圈表示。事项是两条以上矢线的交接点，所以也叫节点，节点不消耗资源，也不占用时间和空间，它只表示某项活动开始或结束的瞬间。网络图中开始的第一个事项称作网络始点事项，它表示一项计划任务的开始。最后一个事项称为网络终点事项，它表示一项计划任务的结束。当然中间的事项就称为中间事项。
事项需要进行编号，以便于识别、检查和进行计算。
编号一般采用由小到大、连续或非连续编号，非连续编号的优点是网络图局部的修改不影响整个网络图的编号。
（3）线路（或路线） 线路是指从网络始点事项开始，顺着矢线方向到网络终点事项为止，中间是由一系列首尾相连的节点和矢线所组成的通道。线路中各项活动的作业时间之和就是该线路所需要的时间。在一个网络中可能有若干条线路，每条线路所需要的时间有长和短，其中时间最长的一条线路称作关键线路（CP）。关键线路所需的时间，也就是完成整个计划任务所需要的总工期。位于关键线路上的活动叫关键活动，它们完成的快慢直接影响整个工程的工期。
1.1.2 绘制网络图的规则
（1）网络逻辑 网络逻辑是指一项工作与其他有关工作之间相互联系与制约的关系，也就是各项工作在工艺上、技术上所要求的顺序关系。
（2）技术规则
1）对节点编号时，一般应使一项活动的箭头（终点）序号数大于箭尾（起点）的序号数。
2）节点的编号不应有重复。在某两个确定数码的节点间，只允许有一项活动即一根矢线。为了便于修改，节点的编号可跳跃。
3）编号应满足统一性要求，即一个网络图中只能用一种文字进行节点的编号。4）在网络图中不能出现循环线路（或称闭合回路），即矢线从某一节点出发，只能自左向右往前，不能反方向又重新回到该节点上去。
5）矢线的首尾都必须有节点。进入某一点的矢线，其活动全部完成后，从该节点引出新的矢线，活动才能开始，不能从一条矢线的中间引出另一条矢线来。
6）网络图中应当正确地反映各项活动之间的相互联系和相互制约的逻辑矢线。
7）网络图中除了表示整个工程开工的起始事件及竣工的结束事件以外，不允许存在处于自由端状的所谓“尾巴事件”（图5.3中的⑤）及“尽头事件”（图5.3中的③）。
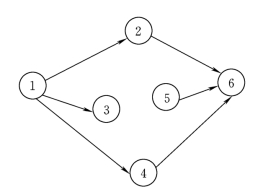
图5.3 某工程网络计划图
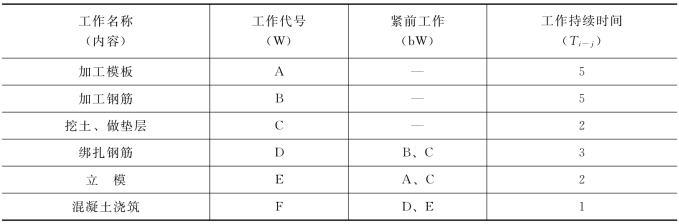
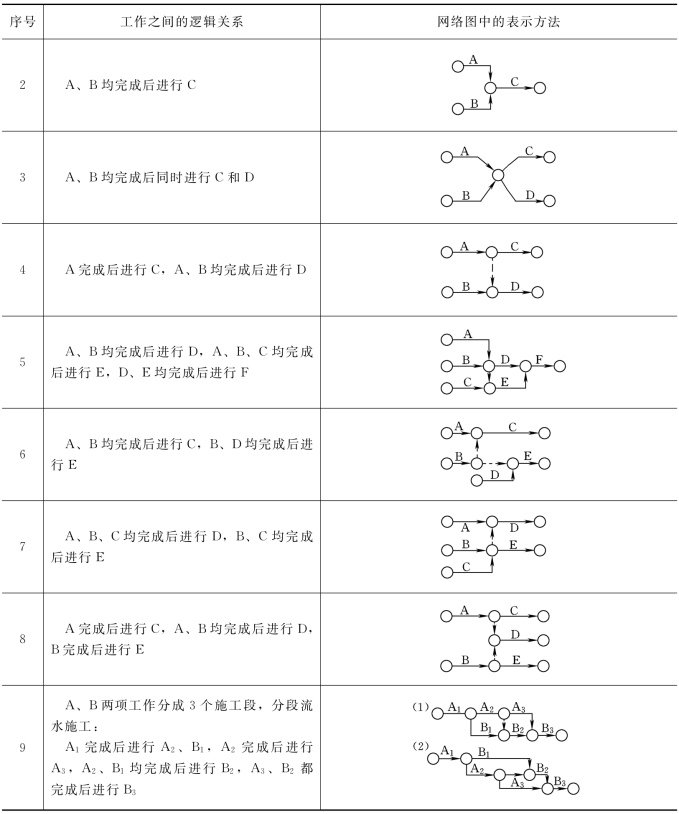
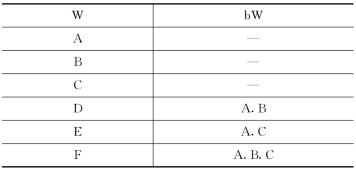
在工程实际的网络计划图中，各项工作之间的逻辑关系是复杂多变的，表5.3所列的是网络计划图中常见的一些工作关系的表示方法。各工作名称以字母表示，供绘双代号网络计划图时参考。
表5.3 常见工作逻辑关系的表示方法
续表
【例5.1】 试对表5.4所代表的施工计划进行网络图的绘制。
表5.4 某工程施工计划表
解：依照上述各项规则绘制网络图如图5.4所示。
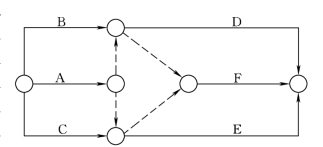
图5.4 某工程网络计划图
1.1.3 时间参数计算及关键线路（CP）
正确绘制代表工程项目进度计划的双代号网络图，只是把工程项目工作之间的逻辑关系用网络计划的形式表达出来了。网络计划技术是一种定量分析方法，它可以为工程计划管理提供一系列重要的定量信息，而这些定量信息是通过网络计划图时间参数计算以后获得的。网络计划的时间参数有：a.最早可能开工时间ES；b.最早可能完工时间EF；c.最迟必须完工时间LF；d.最迟必须开工时间LS；e.总时差TF；f.自由时差FF。研究时间参数的目的是为了确定影响施工进度的关键项目，找出施工时间最长的关键线路，为网络计划进一步优化调整提供科学依据。关键线路从始端贯通整个网络图至终端，在网络图上用粗箭线表示。在关键线路上，每一个项目都是关键项目，延误其工期将延误整个工程的工期。一个网络计划的关键线路至少有一条，有时可能有多条。
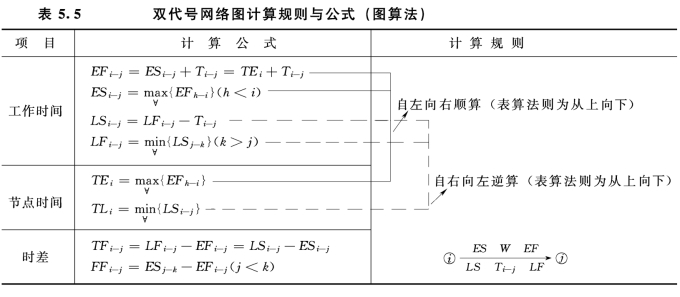
双代号网络图的计算规则与公式如表5.5所示。
网络图的计算方法有多种，可以直接在图上进行，也可用现成的表格计算出。下面以某工程的进度计划网络图为例，说明常用的表算法、标号法和图算法的运算过程。网络图如图5.5所示。
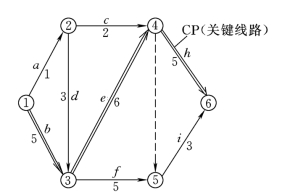
图5.5 某工程进度网络图
（1）表算法 计算过程与结果如表5.6所示。
表5.6 某工程网络图表算法成果表(www.xing528.com)
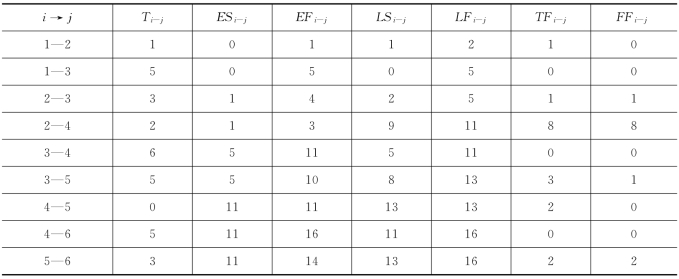
计算结果表明，该工程总工期为16个单位时间，关键线路为：①→③→④→⑥，表算法的优点是一次计算能获取所有的结果与信息，从而为进度控制和优化计算提供技术参数。
（2）标号法 工程中的标号法是采用的双标号法，即用源节点（指已得出标号值的节点）为第一标号，用计算值（标号值）作为第二标号。计算步骤如下：
第一步：令b1=0（b1为起始节点的标号值）；
第二步：计算其他节点的标号值：bj=[bi+Ti-j]max；
第三步：工期Tc=bn（bn为终节点的标号值），关键线路可从网络图的终节点开始，逆箭头方向按源节点确定。
本工程网络图的标号法计算结果如图5.6所示。
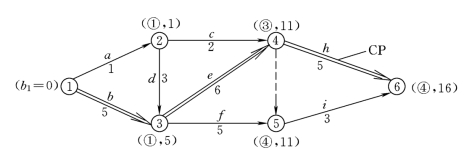
图5.6 某工程网络图标号法计算结果
（3）图算法 图算法可直接在图上进行，适用于一些较简单的网络图。仍以上例为例，其计算过程和结果如图5.7所示。
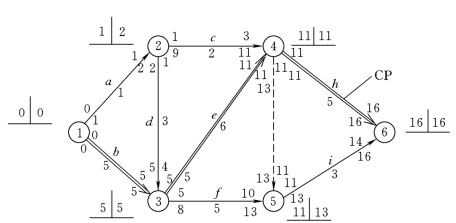
图5.7 某工程网络图图算法计算结果
1.1.4 网络图的优化
网络图的优化是指在既定的条件下，对工程进度计划利用网络图和时差不断调整与改善，使之达到工期、成本目标和资源的最优化利用的综合目标趋优的过程。工期与直接成本C2、间接成本C1之间的关系，如图5.8所示。
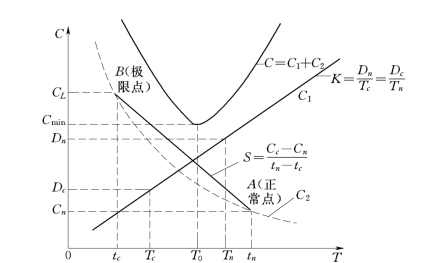
图5.8 网络优化示意图
C1—间接成本与工期的关系曲线；C2—直接成本与工期的关系曲线；C—总成本与工期的关系曲线；S—C2的近似曲线的变化率（即单位时间上所需的直接成本）；K—间接费用的变化率
下面以工期与成本的优化为例说明其过程。优化应遵循以下原则：
1）必须压缩关键工作的持续时间Ti-j（i-j∈CP），才能达到缩短工期的目的，且只能压缩有可能被压缩的工作，即压缩tn＞tc的工作。
2）压缩直接费用率（S）＜间接费用率（K）的工作，这样可达到既能缩短工期，同时在一定范围内又可使总费用最省的目的。
3）优化时被压缩工作的持续时间所受到的限制条件：①压缩后，该工作的Ti-j不能小于其极限时间；②压缩后，该工作的关键性不能改变；③如果存在n条CP，应取这些线路上可压缩时间的最小值，同时在所有的CP上进行压缩；④时差限制条件：CP上可压缩的时间不能大于CP上的FFmin值。
4）优化过程中停止压缩的条件：a.如果是工期有限制条件时，例如合同工期，则压至Tcp=[Th]公式中，Tcp为计算工期。即CP的总长度，Th为合同工期。b.当工期和资源供应均无限制时，则压至所有的工作的直接费用率Si-j≥K（直接费用率）时为止。此时的进度计划为最优方案。
【例5.2】 某水利水电工程控制性的施工进度计划及其有关资料如表5.7所示，设K=1万元/单位时间，[Th]=9个单位时间，试进行T-C优化计算。
解：（1）绘出进度计划的网络图（如图5.9）并计算Si-j（见表5.7）。
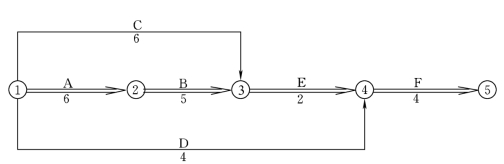
图5.9 进度计划的网络图
（2）用表算法计算时参（过程略）
得知时参如表5.7所列[见（1）栏]，且其关键线路为①→②→③→④→⑤（如图5.9中双箭线）工期Tcp=17。
在未优化的情况下，原进度计划17个单位时间相应的费用为：
C0=∑Cn+C2=22.85+17K=39.85（万元）
（3）优化计算。
1）第一次压缩。因为Smin=SA=0.25，SE=0.35（第二个最小值），且A、E工作各自可压缩时间分别为4和1个单位时间，下同。又因为FFmin=5，所以本次共可压缩时间为5。故令：
。压缩后，网络图时计算，时差如表5.7所列[见（2）栏]，且并没有改变，但是工期由原17压缩为12。相应的总费用如下：
C1=C0+∑ΔCi-ΔCj
=39.85+4×0.25+1×0.35-5×1=36.2（万元）＜C0
式中：ΔCi为第i个被压缩工作压缩后引起直接费用的增加值；ΔCj为总工期被缩短后所引起间接费用的减少值。
2）第二次压缩。A、E工作均已达极限工期，不能再压，又因为SB＜SF，所以可将B压缩1个单位时间，经计算知（见表5.7所列）：工期为11，关键线路由原来1条增加至2条，即新增关键线路为：①→③→④→⑤。相应的总费用为：
表5.7 某工程施工进度计划及有关资料表
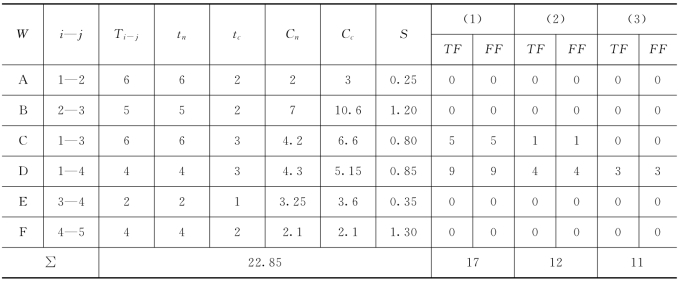
C2=C1+1.2×1-1×1=36.4（万元）＞C1
可见，总费用的Cmin其相应的最优工期应在第1～第12之间。
3）第三次压缩。因为仅有TFD=FFD=3，所以从理论上可压缩3个单位时间。但是根据实际需要，本次压缩仅压2个单位时间即可。即令
（两条CP上要压缩相同的时间）。
压缩后，其网络图用标号法计算结果如下（如图5.10所示）：
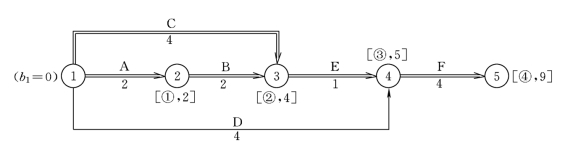
图5.10 优化成果图
C3=C2+1.2×2+0.8×2-2×1=38.4（万元）
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
