敏感性分析：经济效益评价指标的风险评估

敏感性分析是分析预测项目主要因素发生变化时对经济效益评价指标的影响，从中找出敏感因素，并确定其影响程度。可能发生变化的主要因素有产品产量（生产负荷）、产品价格主要原材料或动力价格、可变成本、固定资产投资、建设工期及外汇牌价等。

敏感性分析亦称之为灵敏度分析，它可以判断已选定方案在主要经济效果等指标方面的稳定程度，还可以检验不同基本数据情况下对方案经济和财务方面的影响。

敏感性分析的目的，就是要在诸多的不确定的因素中，找出对经济效果指标反应敏感和反应不敏感的因素，并判明其对项目经济效果的影响程度。它是经济决策中常用的一种不确定性分析方法。

在实际工作中，可运用敏感性分析图来显示敏感因素。敏感性分析图即表示建设项目相关因素的不确定性对其经济效果指标影响程度的图示，如图2.26所示。

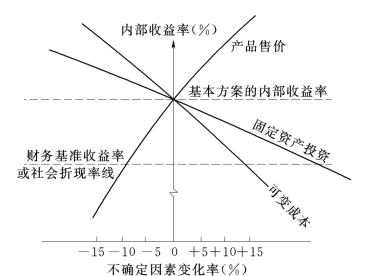
图2.26　敏感性分析图（示例）

以项目的全部投资内部收益率为纵坐标，以几种不确定因素的变化率（百分数）为横坐标，根据敏感性分析表所列数据绘图，并标出财务基准收益率线或社会折现率线。

图中某种因素对全部投资内部收益率的影响曲线与基准收益率线或社会折现率线的交点（临界点），为允许该种因素变化的最大幅度，即极限变化。

进行分析评价一般是先计算出基本情况下的评价指标，然后使选定的因素在确定的范围内变化，并计算出相应的评价指标。

【例2.20】 某方案各参数的最初预测值如表2.12所示，设投资额的利率不变，试对其他参数逐一进行敏感性分析。

表2.12　单位：万元

解：因为NPV=-17+A1（P/A，i，n）-A2（P/A，i，n）+L（P/F，i，n）

式中：n，A1，A2，L分别为待定分析的不确定性因素，设其最大变化范围为：-30%→+30%，每次只改变其中一个参数时，NPV的敏感性分析结果如图2.27所示。（方案的单参数变化敏感性计算结果见表2.13所示）

表2.13　单位：万元

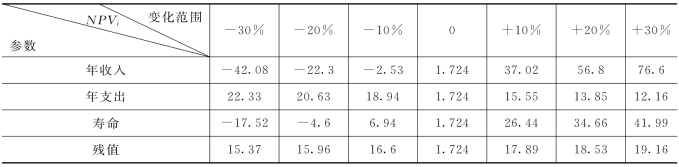
从图2.27可以看出，NPV对年收入A1和寿命n的变化最为敏感，而对年支出A2和残值L的变化反映相对而言不太敏感。

图2.27

将各曲线与横坐标轴的交点坐标称之为临界值，参数的临界值是使净现值NPV由正→负（或由负→正）发生转折变化的关键值。本例中，A1参数的临界值约等于-10%，n的临界值约等于-15%。也就是说，只要年收入的减少不超过10%，寿命期n的变化不要超过-15%，该投资方案便能保证NPV＞0而盈利。(www.xing528.com)

【例2.21】 某施工企业为评价分析一个投资项目方案，初拟出一个基本方案如图2.28所示，设i=8%，试进行多因素的敏感性分析。

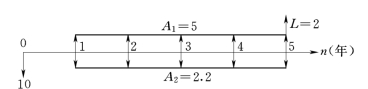
图2.28（单位：万元）

解：（1）双因素敏感性分析。

工程中，将同时改变两个不确定性因素对某经济指标的影响分析，称为双因素敏感性分析。通过例2.21分析可知，单因素敏感性分析，从几何意义上反映为一条“敏感线”，而双因素敏感性分析在几何意义上反映为“敏感面”，从而可得到盈利区和亏损区，则很方便地知道所评价的方案对哪一个因素最为敏感。

现设初始投资的变化增量为x，年收入A1的变化增量为y，则：

NAV=-10（1+x）（A/P，8%，5）+5（1+y）-2.2+2（A/F，8%，5）

=0.636-2.505x+5y

令NAV=0。可解出，x=0.253，y=-0.1272。

NAV=0为投资方案盈亏平衡线（见图2.29），它把x-y平面分为两个区域：盈利区和亏损区。

从图2.29可看出，项目方案对年收入A1最为敏感。

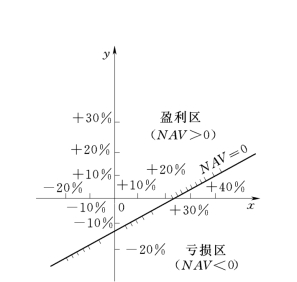
图2.29

（2）三因素敏感性分析。

除上述初始投资变化为x，年收入变化为y外，现设年支出A2的变化为z，则有：

A=NAV=-10（1+x）（A/P，8%，5）+5（1+y）-2.2（1+z）+2（A/P，8%，5）

=0.636-2.505x+5y-2.2z

满足方案可行的条件是：NAV≥0，所以上式为一空间平面方程，从而有x=0.253，y=-0.127，z=0.3。此空间平面将三维空间分为两部分（如图2.30所示）。相比之下，投资方案对年收入最为敏感，其次是初投资，再次为年费用。

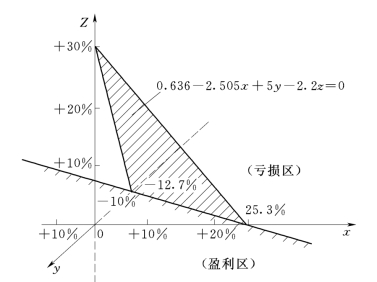
图2.30