现值法是现代计算经济中最基本的,应用范围最广泛的一种经济分析方法,几乎适用于任何技术经济问题。工程中,当人们要想知道工程项目或施工方案在其寿命期范围内的收益或费用的现值、股票或债券的当天价值等时,用此方法最为适宜。当然,现值法进行经济分析计算时,是在下列假设条件的基础上进行的。
现值总额P发生在初期,而各期收支额A和终值总额F发生在末期。过去花掉的费用是沉没费用(指以往发生的与当前决策无关的费用),它对现在和将来的费用影响可忽略不计。
一般假定所需资金均是借来的,同时严格区别投资与集资这几类问题。
现值法的基本思想是将分析对象在其寿命期内的所用现金收入和支出都按基准利率(亦称基准贴现率)折算为现值(贴现计算),用NPV或NPW表示,其计算公式为:

式中:CI为现金流入量;CO为现金流出量;i0为目标收益率(或基准收益率)。
显见,如果NPV>0说明投资不但获得预期的投资收益,而且还得到正值差额的现金利益,反之亦然,且NPV越大,盈利越大。如果NPV=0,说明刚好满足利益要求,即盈亏平衡。
综上可得出如下判据:
当NPV≥0时,方案可考虑接受。
当NPV<0时,方案不可行。
对于多种互斥方案,应优先选NPV最大者。
现值法不仅考虑了方案的整个寿命期,而且考虑了方案整个分析期内的经营情况。
【例2.1】 某方案的各年现金流量如图2.3所示,试用NPV判断其经济性。已知i0=10%,单位;万元。

图2.3 例2.1现金流量图
解:由式(2.18)有:

所以该方案在经济效果上是可以考虑的。
应用现值法时,必须重视以下几点。首先是方案的所有货币资金都是要折算到同一基准年,工程中一般是取工程开工的年份为基准年。其次是所有的现值计算都要采用相同的基准贴现率(资金报酬率,目标收益率),最后是在现值分析中,必须慎重考虑分析周期,如果各方面的分析期不同,则应进行相应的换算使之具有可比性。
一般的,工程中常遇到的分析期有如下三种。
2.1.1 分析期等于使用期
在这种情况也就是所比较的方案其使用周期相等,现用下例说明分析方法。
【例2.2】 某施工企业选购施工机械用于对外经营,有A、B两种型号,其资金情况如表2.2所示,设i0=8%,问选购何种类型的机械为宜。
表2.2 机械资金情况表

解:现金流量图的绘制如图2.4所示

图2.4 现金流量图
NPV(A)=-9+4.5(P/A,8%,3)=-9+4.5×2.577=2.6(万元)
NPV(B)=-14.46+6(P/A,8%,3)+2(P/F,8%,3)
=-14.46+6×2.577+2×0.794=2.6(万元)
显见,选购A、B两种型号的施工机械均满足最低吸引力的收益率8%(因为NPV(A)=NPV(B)且为正数)此时,应该考虑机械的价格差异,因为选购A型机械可少投资近5万元,故应选购A型号施工机械。
2.1.2 分析期不等于使用周期
分析期与试用期不同的是工程中常见的情况,为了使比较方案具有可比性,目前工程中的处理办法是最小公倍数法。通过下例说明其分析过程与方法。
【例2.3】 若例2.2中机械B的使用期为6年,其他条件不变,试进行施工机械的选购。
解:因为A、B两类机械的使用期分别为3年和6年,所以分析期取两者的最小公倍数6年。在6年内A机械现金流量再重复一次(见图2.5,单位:万元)

图2.5
又因为(https://www.xing528.com)
NPV(A)=-9+4.5(P/A,8%,6)-9(P/F,8%,3)
=-9+4.5×4.623-9×0.794
=4.66(万元)
NPV(B)=-14.45+6(P/A,8%,6)+2(P/F,8%,3)
=-14.45+6×4.623+2×0.63
=14.55(万元)>NPV(A)
所以应选购B型号施工机械较为有利。
一般情况下,用最小公倍数法处理分析期不等于使用周期的问题时可行的。但是当各个方案分析期相差过大,而且两者的最小公倍数也比较大时,就缺乏可比性了,此时应改用其他的方法。
2.1.3 分析周期无限长(即n=∞)
在实际中,有一些问题是相当于n=∞的情况,例如有些固定资产如大坝,桥梁如维修良好,可假定供永久使用,亦即其使用寿命可认为无限长。对此类问题,现值法将按无限的分析周期计算。工程中称之为资本化费用,其公式证明如下:
因为
![]()
当n→∞时

A=P(A/P,i,n)|n→∞=pi 或 p=A/i
【例2.4】 某建筑公司对所承包的项目拟定了两个可供选择的方案(见表2.3)试决策哪个方案为优(取利率为8%)。
表2.3 A、B方案资金费用情况表 单位:万元

则
解:A、B方案的寿命期长达50年,可视为无限长。各方案的现金流量图如图2.6所示。

因为
|NPV(B)|>|NPV(A)|

图2.6
所以知A方案优,即A方案较B方案可节省费用105.86万元。
从以上分析计算知,NPV仅衡量了项目的净收益(或净支出)的大小,而不能直接反映资金的利用率。实际工程中,我们不仅要计算出项目方案的净现值,而且还要进一步把它除以相应总投资的现值,得到一种折现收益率方案方可进行比较选优。
折现收益率也称之为净现值率,其数学表达式为(设Kt为第t年的投资支出):
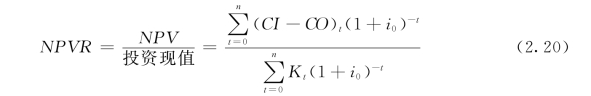
在方案的技术经济分析中,也常用NPVR来确定多种方案的优先顺序,NPVR大的项目方案应优先考虑。NPVR的工程含义是,投资方案除保证有一定的收益率外,每单位投资尚可获得取得相当的额外收益。
【例2.5】 某施工企业拟有两个可供选择的投资方案,A方案初投资1500万元,每年可获得500万元的收益。B方案初投资1850万元,每年可获得600万元的收益。两方案的寿命期均为5年,收益率为10%,试比较两者的优劣。
解:(1)按NPV进行比较
NPV(A)=500(P/V,10%,5)-1500=395.5(万元)
NPV(B)=600(P/V,10%,5)-1850=424.4(万元)>NPV(A)
B优于A,但是B较A多投资350万元,尚需要进一步分析。
(2)按NPVR进行比较
NPVR(A)=395.5/1500=0.264
NPVR(B)=424.4/1850=0.23<NPVR(A)
所以A优于B,可见与上述结论相反,故而当投资额不相等且相差较大时,往往还要进行NPVR的计算,经综合比较分析后方可得出正确的结论。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




