1.尺寸链基础知识
由相互联系且按一定顺序排列的尺寸形成的封闭尺寸图形,称为尺寸链。尺寸链中的每一个尺寸称为环。对于尺寸链如果还没有印象,但凡看过零件图,都会知道图样上有一个空白尺寸,这个尺寸很重要。从这个空白尺寸的一端出发,中间通过一个个的确定尺寸,如果能回到空白尺寸的另一端,再加上空白尺寸本身,就形成了一个链,这就是尺寸链。如果这个尺寸链存在,说明图样上不缺尺寸;如果链断了,则图样上少了确定的尺寸,需要补上。那么一张图样上有多少个尺寸链呢?答案很明确:就是有多少个空白尺寸,就有多少个尺寸链;即图样上的尺寸链中,一个链上只允许有一个空白尺寸。
再说说尺寸链是如何组成的以及尺寸之间有什么相互关系。尺寸链中有两种尺寸,一个是确定的尺寸,一个是空白尺寸。确定的尺寸是直接得到(或看到)的尺寸,而空白尺寸则是被确定尺寸所决定的。可见,一个尺寸链由两个部分组成,那些确定的尺寸称为组成环;间接得到的尺寸,如空白尺寸,称为封闭环,用A0表示。一个链中,封闭环只有一个。
封闭环的尺寸受各组成环的影响。影响的结果是:假定有一个组成环的尺寸为A±ΔA,当A尺寸增大为A+ΔA时,封闭环的尺寸也跟着增大,当A尺寸减小为A-ΔA时,封闭环的尺寸也跟着减小;再假定有一个尺寸为B±ΔB,当B尺寸增大为B+ΔB时,封闭环的尺寸反而减小。由此可以得出结论:尺寸链中的组成环有两种,一种是当其增大时,封闭环也增大,就称这个组成环为增环,用→A表示;另一种是当其增大时,封闭环减小,就称这个组成环为减环,用A←表示。
2.尺寸链的分类
尺寸链在机械设计、机械加工和机械装配中应用非常广泛,按应用场合不同可以分为三种。
(1)设计尺寸链 在零件图上的尺寸链就是设计尺寸链。其中前面提到的空白尺寸,就是设计尺寸链中的封闭环。
(2)装配尺寸链 全部组成环为不同零件设计尺寸所形成的尺寸链,称为装配尺寸链。装配尺寸链的封闭环很明确,也很具体。装配工人天天装配,就是在保证这个封闭环达到要求,即达到检验指标。
(3)工艺尺寸链 全部组成环为同一零件上的工艺尺寸所组成的尺寸链,称为工艺尺寸链。所谓工艺尺寸泛指在加工过程中使用的尺寸,包括定位尺寸、工序尺寸,测量尺寸等,都可以应用工艺尺寸链的计算得到。
工艺尺寸链中的组成环和封闭环是由加工过程决定的。图样上的封闭环,在加工过程中不一定是封闭环,可能变成组成环。因此要给工艺尺寸链中的各环下一个确切定义,即在工艺尺寸链中,通过加工过程可以直接保证的尺寸,为组成环,被间接保证的尺寸为封闭环。下面通过一个实例来说明。
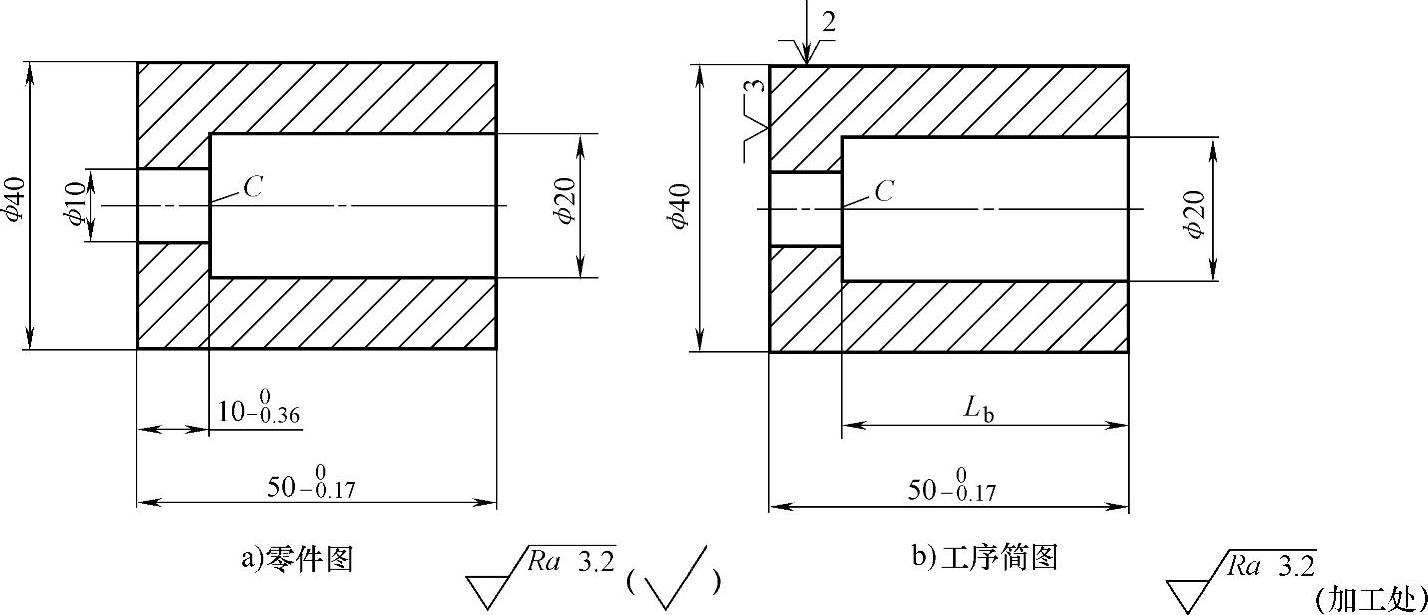
图8-20 工艺尺寸链分析图例
图8-20a为零件图,图8-20b为工序简图。在简图上表明了本道工序的加工内容。工件左端面为三点定位(靠在卡盘端面上),外圆两点定位(用自定心卡盘夹紧),加工顺序为先加工工件右端面,保证尺寸500-0.17mm,然后加工ϕ20mm内孔及端面C。按零件图要求,在加工中应该直接保证ϕ10mm小孔的长度尺寸100-0.36mm。但由于ϕ10mm孔太小,无法测量,而C端面与工件右端面的尺寸Lb用游标卡尺上的测深度尺,轻而易举地测量到,但测量基准是右端面,与设计基准不重合。这就出现了如何确定Lb尺寸和公差的问题,才能保证ϕ10mm小孔的长度满足100-0.36mm的要求?这就需要利用工艺尺寸链来计算。
3.尺寸链计算公式与计算方法
(1)建立尺寸链 要计算尺寸链,首先要建立尺寸链图形。图8-20a零件图的设计尺寸链和图8-20b工序简图的工艺尺寸链如图8-21所示。为了区别,设计尺寸链加“′”表示。由尺寸链可知,零件图中的封闭环A′0,在工艺尺寸链为组成环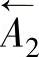 ,两者在性质上已经不同。前者是间接保证的尺寸,后者是直接保证的尺寸。同理,在零件图上直接保证的尺寸
,两者在性质上已经不同。前者是间接保证的尺寸,后者是直接保证的尺寸。同理,在零件图上直接保证的尺寸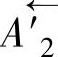 ,在工艺尺寸链中变为封闭环A0。这种改变是因加工的需要而采用的,使C面的测量基准与设计基准不重合。此时若盲目地以设计尺寸链确定工艺尺寸链中的
,在工艺尺寸链中变为封闭环A0。这种改变是因加工的需要而采用的,使C面的测量基准与设计基准不重合。此时若盲目地以设计尺寸链确定工艺尺寸链中的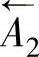 ,把这个尺寸误当作封闭环A′0处理,就会犯致命错误,按此加工就会产生大量废品。这是要格外注意的。关于这个问题,在后面还将进一步讨论。
,把这个尺寸误当作封闭环A′0处理,就会犯致命错误,按此加工就会产生大量废品。这是要格外注意的。关于这个问题,在后面还将进一步讨论。
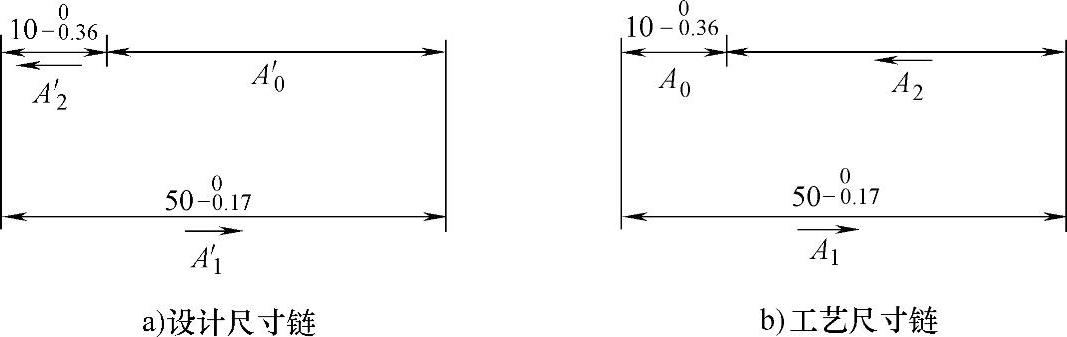
图8-21 零件的设计尺寸链与工艺尺寸链
(2)尺寸链基本计算公式 在工艺尺寸链计算中,常用的方法是极值法。基本计算公式如下。
1)封闭环的基本尺寸A0。封闭环的基本尺寸等于所有增环的基本尺寸之和减去所有减环基本尺寸之和,即
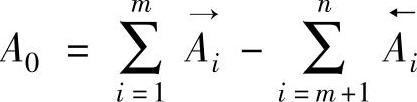
式中 m——增环的环数;
n——组成环的环数。
2)封闭环的最大极限尺寸A0max。封闭环的最大极限尺寸等于所有增环最大极限尺寸之和减去所有减环最小极限尺寸之和,即
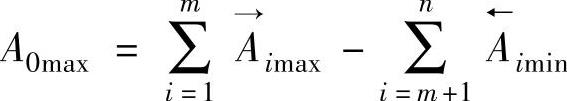
3)封闭环的最小极限尺寸A0min。封闭环的最小极限尺寸等于所有增环最小极限尺寸之和减去所有减环最大极限尺寸之和,即
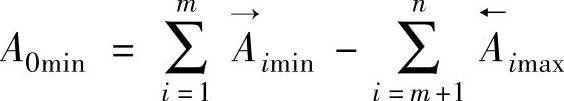
4)封闭环的上偏差ES(A0)。封闭环的上偏差等于所有增环上偏差之和减去所有减环下偏差之和,即
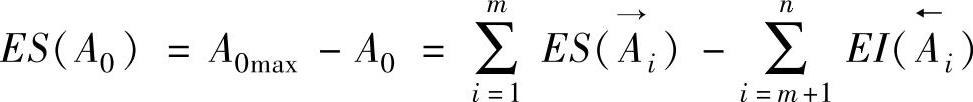
5)封闭环的下偏差EI(A0)。封闭环的下偏差等于所有增环下偏差之和减去所有减环上偏差之和,即
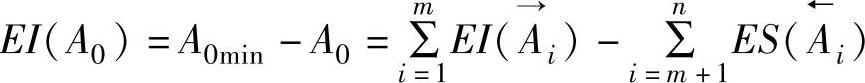
6)封闭环的公差T0。封闭环的公差等于所有组成环公差之和,即
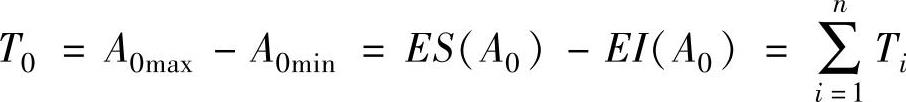
(3)工艺尺寸链的计算形式 在计算工艺尺寸链时,有以下三种计算形式。
1)正计算。已知各组成环的尺寸和上下偏差,计算封闭环尺寸及其上下偏差,其结果是唯一的。这种情况主要用来验证工序尺寸及其上下偏差是否满足设计尺寸要求,即用于设计尺寸的校验。(https://www.xing528.com)
2)反计算。已知封闭环的尺寸及其上下偏差,计算各组成环上下偏差。这种情况实际上是将封闭环的公差值合理地分配给各组成环,主要用于根据机床的装配精度,确定零件各设计尺寸及其上下偏差及其上下偏差的计算,以及根据某一间接保证的设计尺寸,确定工序尺寸及其上下偏差的计算。
反计算时,封闭环公差的分配方法有三种。
①按等公差法分配。将封闭环的公差值平均分配给各个组成环。即每个组成环的公差值相等。此方法比较方便,但只适用于各组成环尺寸及加工难易程度相关不大的情况。
②按等精度法分配。按同一精度等级来分配各组成环的公差,即每个组成环的精度等级均相等。
③按经济精度分配。将封闭环的公差按照各组成环的经济精度公差值进行分配。然后加以适当调整,使得组成环公差值之和等于或小于封闭环公差值。这种方法从工艺上考虑是比较合理的。
3)中间计算。已知封闭环和部分组成环的尺寸及其上下偏差,计算某一个组成环尺寸及其上下偏差。此方法应用最广,用于加工中基准不重合时工序尺寸及其上下偏差的计算。
4.尺寸链计算举例
图8-20a所示的设计尺寸链计算属于正计算,而图8-20b所示的工艺尺寸链属于中间计算,具体计算过程如下。
(1)设计尺寸链的计算(正计算)
1)封闭环基本尺寸 A′0=(50-10)mm=40mm
2)封闭环最大极限尺寸 A′0max=[(50+0)-(10-0.36)]mm=(40+0.36)mm
3)封闭环最小极限尺寸 A′0min=[(50-0.17)-(10+0)]mm=(40-0.17)mm
4)封闭环的上偏差 ES′(A0)=[(0)-(-0.36)]mm=+0.36mm
5)封闭环的下偏差 EI′(A0)=[(-0.17)-(0)]mm=-0.17mm
6)封闭环公差 T′0=T′1+T′2=[(0.17)+(0.36)]mm=0.53mm
(2)工艺尺寸链的计算(中间计算)
1)封闭环基本尺寸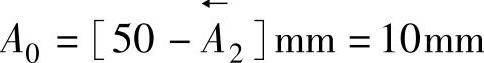
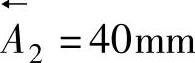
2)封闭环最大极限尺寸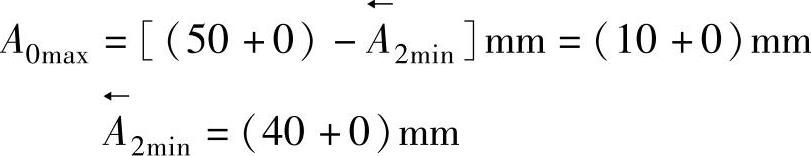
3)封闭环最小极限尺寸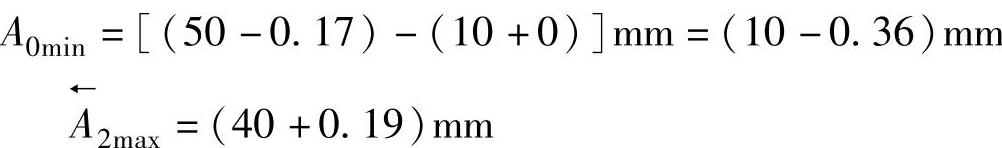
4)封闭环的上偏差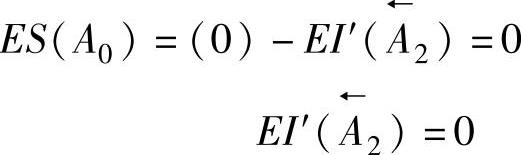
5)封闭环的下偏差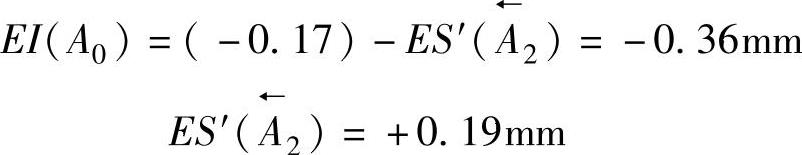
6)封闭环公差 T0=[(0.17)+T2]mm=0.36mm
T2=0.19mm
(3)封闭环的公差带 图8-22所示同一基本尺寸(A′0或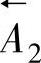 )为40mm的不同公差带图。这个尺寸在设计尺寸链中是封闭环,即A′0=40+0.36-0.17mm;在工艺尺寸链中是减环,即
)为40mm的不同公差带图。这个尺寸在设计尺寸链中是封闭环,即A′0=40+0.36-0.17mm;在工艺尺寸链中是减环,即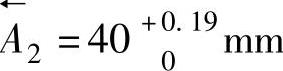 。加工时必须按照
。加工时必须按照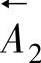 给定的尺寸及上下偏差进行,否则就会出废品。如果错误地按A′0尺寸及上下偏差加工,就会出现以下三种情况。
给定的尺寸及上下偏差进行,否则就会出废品。如果错误地按A′0尺寸及上下偏差加工,就会出现以下三种情况。
1)加工后工件的尺寸落在(40-0.17)~(40-0)mm区间时,则尺寸小,不能间接保证100-0.36mm,合格,需要返修。
2)加工后工件的尺寸落在(40+0)~(40+0.19)mm区间时,则尺寸合格,可以间接保证100-0.36mm尺寸合格。
3)加工后工件的尺寸落在(40+0.19)~(40+0.36)mm区间时,尺寸大,不能间接保证100-0.36mm尺寸,而且不可返修,为废品。
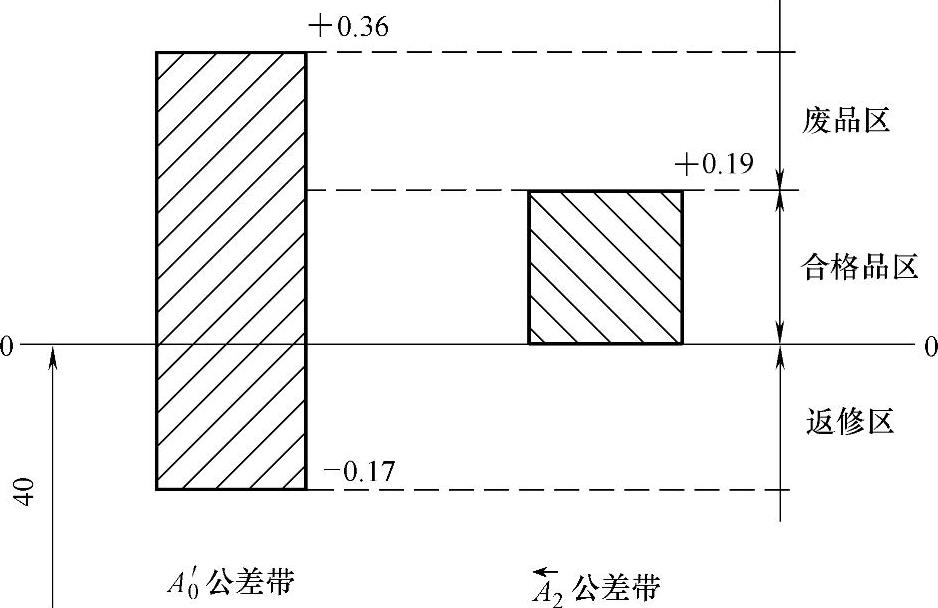
图8-22 尺寸链的环公差带
确定工序尺寸的方法很多,有关工序尺寸计算参数与计算公式,已在国家标准GB/T5847—2004中作出了规定,并对于详细解决所有工序尺寸问题都有相应的范例,读者可自行参阅。
(4)绘制工序简图 图8-20b的工序简图中,工序尺寸是Lb标注的,那时因为那时还没有计算出来。Lb就是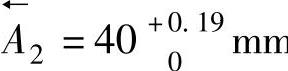 工序尺寸。将这个尺寸标注在工序简图上,这个简图就是一个完整的工序简图,如图8-23所示。
工序尺寸。将这个尺寸标注在工序简图上,这个简图就是一个完整的工序简图,如图8-23所示。
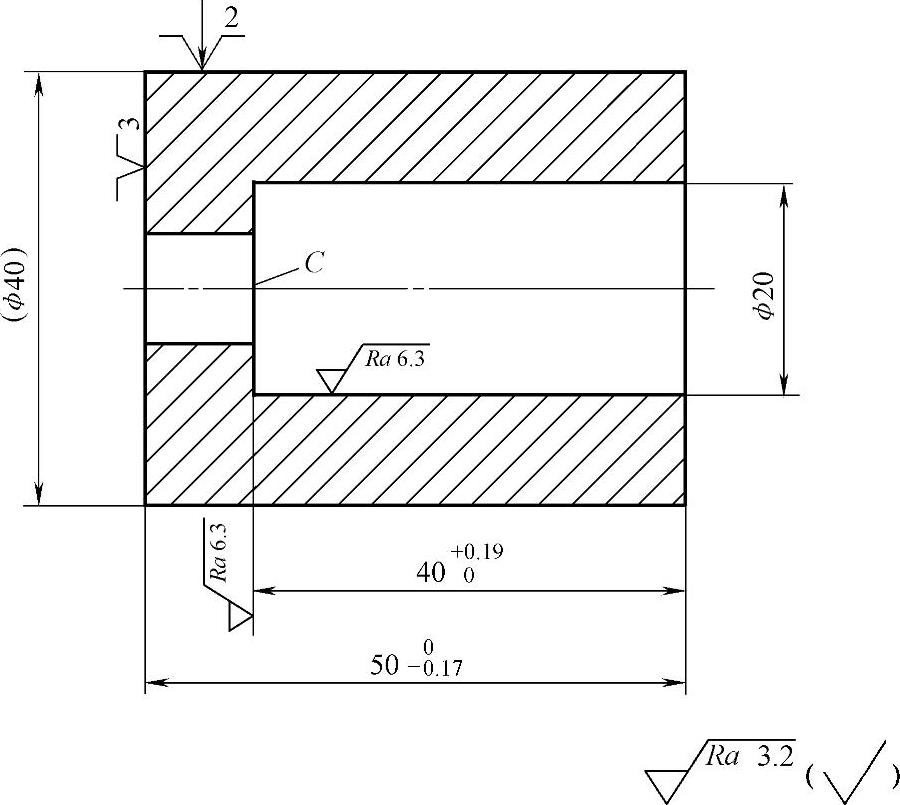
图8-23 工序简图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




