机器人单关节位置伺服控制优化方法

大部分机器人的控制系统像PUMA机器人一样，分为上位机和下位机。从运动控制的角度看，上位机作运动规划，并将手部的运动转化成各关节的运动，按控制周期传给下位机；下位机进行运动的插补运算及对关节进行伺服控制，所以常用多轴运动控制器作为机器人的关节控制器。多轴运动控制器的各轴伺服控制也是独立的，每个轴对应一个关节。这种控制方法并没有考虑实际机器人各关节的耦合作用，因此对于高速运动、变载荷控制的伺服性能也不会太好。实际上，可以对单关节机器人作控制设计，对于多关节、高速变载荷的情况，可以在单关节控制的基础上作补偿。

控制器设计的目的是使控制系统具有良好的伺服性能。机器人伺服系统主要由驱动器、减速器及传动机构、力传感器、角度（位置）传感器、角速度（速度）传感器和计算机组成。其中，传感器可以提供机器人各个臂的位置、运动速度或力的大小信息，将它们与给定的位置、速度或力相比较，则可以得出误差信息。计算机及其接口电路用于采集数据和提供控制量，各种控制算法是由软件完成的。驱动器是系统的控制对象，传动机构及机器人的手臂则是驱动器的负载。目前应用最多的是直流电动机驱动和交流电动机驱动。

1.工业机器人对关节驱动电动机的要求

机器人电动伺服驱动系统是利用各种电动机产生的力矩和力，直接或间接地驱动机器人本体，以获得机器人的各种运动的执行机构。

对工业机器人关节驱动的电动机，要求有最大功率重量比和转矩惯量比、高起动转矩、低惯量和较宽广且平滑的调速范围。特别是像机器人末端执行器（手爪），应采用体积、重量尽可能小的电动机。尤其是要求快速响应时，伺服电动机必须具有较高的可靠性和稳定性，并且具有较大的短时过载能力。这是伺服电动机在工业机器人中应用的先决条件。

机器人对关节驱动电动机的主要要求归纳如下：

①快速性。电动机从获得指令信号到完成指令所要求的工作状态的时间应短。响应指令信号的时间越短，电伺服系统的灵敏性越高，快速响应性能越好。一般是以伺服电动机的机电时间常数的大小来说明伺服电动机快速响应的性能的好坏。

②起动转矩惯量比大。在驱动负载的情况下，要求机器人的伺服电动机的起动转矩大、转动惯量小。

③控制特性的连续性和直线性。随着控制信号的变化，电动机的转速能连续变化，有时还需转速与控制信号成正比或近似成正比。

④调速范围宽。能使用于1∶1000～1∶10000的调速范围。

⑤体积小、重量小、轴向尺寸短。

⑥能经受得起苛刻的运行条件，可进行十分频繁的正、反向和加、减速运行，并能在短时间内承受过载。

2.工业机器人驱动所采用的电动机

目前，由于高起动转矩、大转矩、低惯量的交、直流伺服电动机在工业机器人中得到广泛应用，一般负载为100kg以下的工业机器人大多采用电伺服驱动系统。所采用的关节驱动电动机主要是交流伺服电动机、直流伺服电动机、直接驱动电动机和步进电动机。其中，交流伺服电动机、直流伺服电动机、直接驱动电动机（DD）均采用位置闭环控制，一般应用于高精度、高速度的机器人驱动系统中；步进电动机驱动系统多应用于对精度、速度要求不高的小型简易机器人开环系统中。交流伺服电动机由于采用电子换向，无换向火花，在易燃易爆环境中得到了广泛的使用。机器人关节驱动电动机的功率范围一般为0.1～10kW。在工业机器人驱动系统中，所采用的电动机可细分为以下几种：

①交流伺服电动机。包括同步型交流伺服电动机等。

②直流伺服电动机。包括小惯量永磁直流伺服电动机、印制绕组直流伺服电动机、大惯量永磁直流伺服电动机、空心杯电枢直流伺服电动机。

③步进电动机。包括永磁感应步进电动机。

机器人驱动系统要求传动系统间隙小、刚度大、输出转矩高以及减速比大，常用的减速机构有以下几种：

①RV减速机构。

②谐波减速机构。

③摆线针轮减速机构。

④行星齿轮减速机构。

⑤无侧隙减速机构。

⑥蜗轮减速机构。

⑦滚珠丝杠机构。

⑧金属带/齿形减速机构。

⑨球减速机构。

下面以直流伺服电机驱动为例，介绍机器人单关节伺服控制系统。

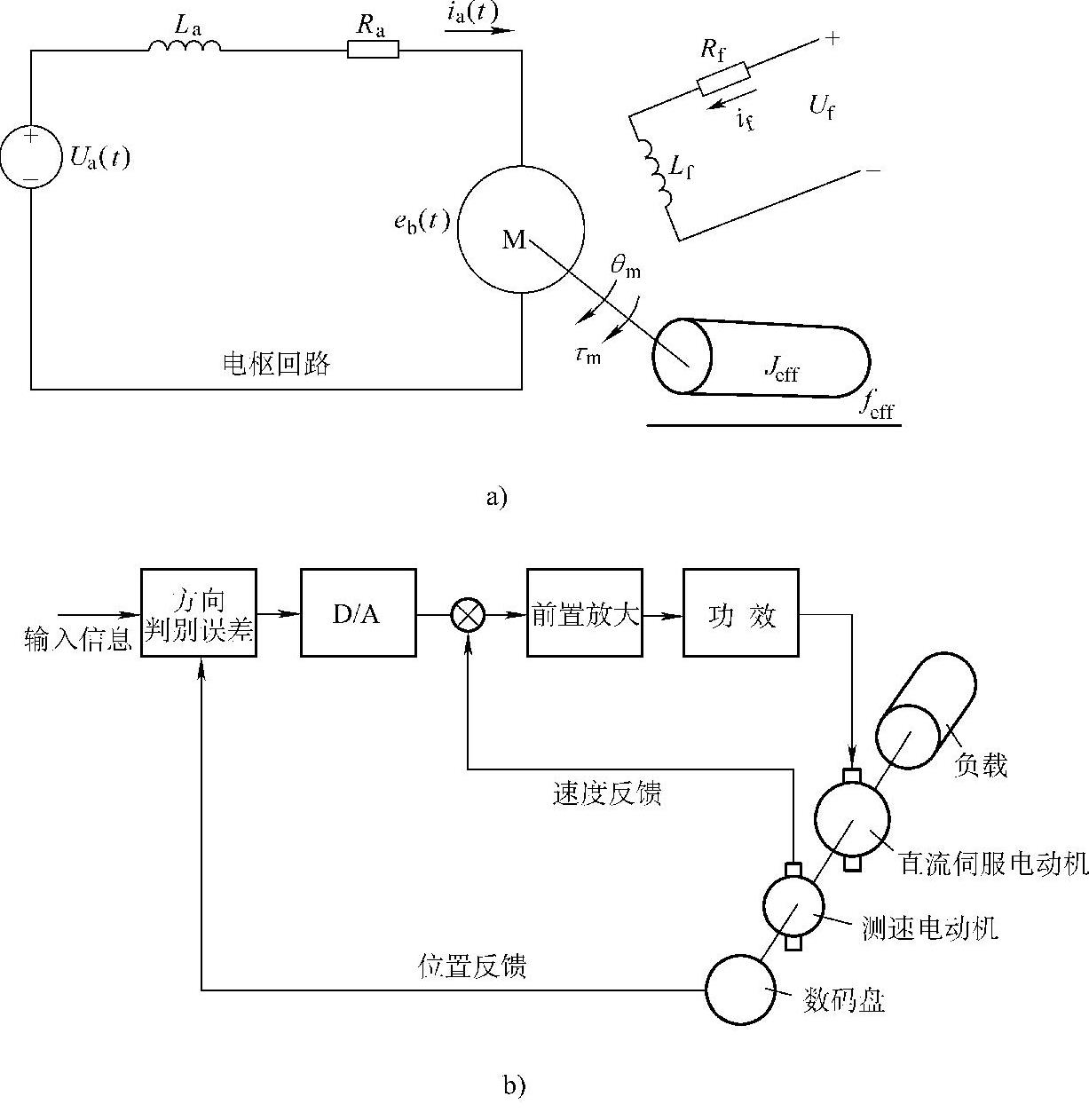
图4-7 直流电动机驱动

a）原理图 b）电枢绕组等效电路

如图4-7所示为驱动单关节的电枢控制直流电动机的等效电路，如图4-8所示为机械传动系统图。两图中符号含义如下：U_a为电枢电压，U_f为激磁电压，L_a为电枢电感，L_f为激磁绕组电感，R_a为电枢电阻，R_f为激磁电阻，i_a为电枢电流，i_f为激磁电流，e_b为反电势，τ_m为电动机输出力矩，θ_m为电动机轴角位移，θ_L为负载轴角位移，J_m为折合到电动机轴的惯性矩，J_L为折合到负载轴的负载惯性矩，f_m为折合到电动机轴的粘性摩擦系数，f_L为折合到负载轴的粘性摩擦系数，z_m为电动机齿轮齿数，z_L为负载齿轮齿数。

从以上所列参数可以得出：

①从电动机轴到负载轴的传动比：

②折合到电动机轴上的总的等效惯性矩J_eff和等效摩擦系数f_eff：

由图4-7和图4-8可以看出，单关节控制系统是一个典型的机电一体化系统，其机械部分的模型由电动机轴上的力矩平衡方程描述。

③电动机电枢绕组内的电压平衡方程：

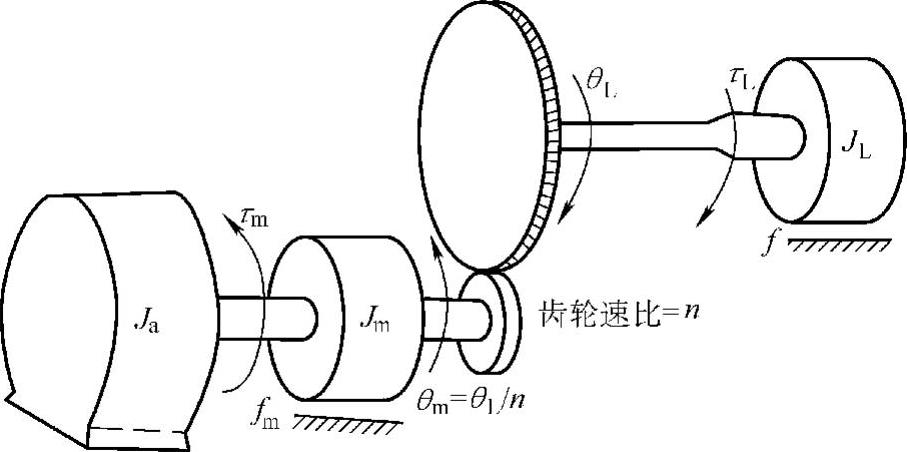
图4-8 机械传动系统

④力矩平衡方程：

⑤耦合关系。

机械部分和电气部分的耦合包括两个方面：一方面是电气对机械的作用，表现在由于电动机轴上产生的力矩随电枢电流线性变化；另一方面是机械对电气的作用，表现在电动机的反电动势与电动机的角速度成正比，即(www.xing528.com)

式中K_a——电动机电流—力矩比例常数；

K_b——感应电势系数。

对式（4-4）～（4-7）进行拉普拉斯变换，得：

重新组合式（4-8）中各方程，得到从电枢电压到电动机轴角位移的传递函数：

由于电动机的电气时间常数大大小于其机械时间常数，故可以忽略电枢的电感L_a的作用。上面方程简化为

由于控制系统的输出是关节角位移（θ_L（s）），它与电枢电压U_a（s）之间的传递关系为：

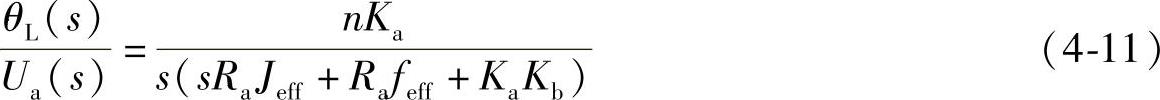
这一方程代表了直流电动机所加电压与关节角位移之间的传递函数。系统的框图如图4-9所示。

图4-9 电动机传递函数

单关节的位置控制是利用由电动机组成的伺服系统使关节的实际角位移跟踪预期的角位移，把伺服误差作为电动机输入信号，产生适当的电压，即

式中K_p——位置反馈增益（V/rad）；

e（t）=θ^d_L（t）-θ_L（t）——系统误差；

n——传动比。

实际上“单位负反馈”把单关节机器人系统从开环系统转变为闭环，如图4-10所示。关节角度的实际值可用光电编码器或电位器测出。

图4-10 单关节反馈控制

对式（4-12）进行拉普拉斯变换，得：

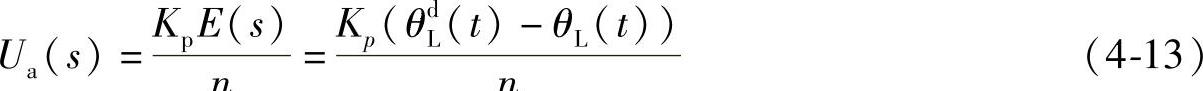
将式（4-13）代入式（4-11）中，得出由误差驱动信号（E（s））与实际位移（θ_L（s））之间的开环传递函数：

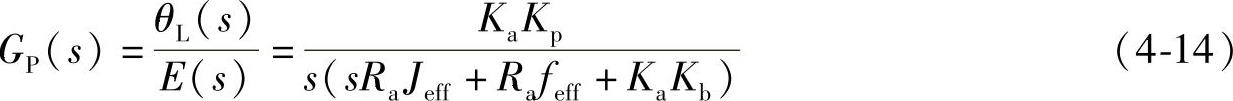
由此可以得出系统的闭环传递函数，它表示实际角位移（θ_L（s））与预期角位移（θ^d_L（s））之间的关系：

式（4-15）表明了单关节机器人的比例控制器是一个二阶系统。当系统参数均为正时，系统总是稳定的。为了改善系统的动态性能，减少静态误差，可以加大位置反馈增益K_p和增加阻尼，再引入位置误差的导数（角速度）作为反馈信号。关节角速度常用测速电动机测出，也可用两次采样周期内的位移数据来近似表示。加上位置反馈和速度反馈之后，关节电动机上所加的电压与位移误差和速度误差成正比，即

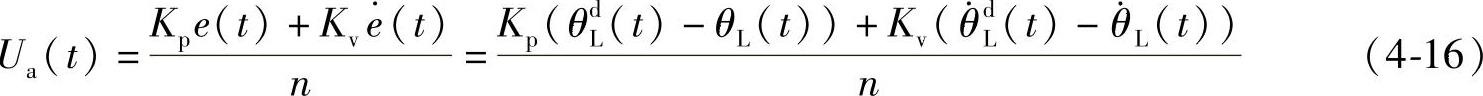
对式（4-16）进行拉普拉斯变换，再把U_a（s）代入式（4-10）中，可得误差驱动信号E（s）与实际位移之间的传递函数：

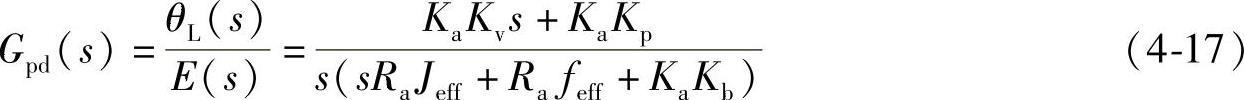
由此可得出表示实际角位移（θ_L（s））与预期角位移（θ^d_L（s））之间的闭环传递函数：

显然，当K_v=0时，式（4-18）变为式（4-15）。

式（4-18）所代表的是一个二阶系统，它具有一个有限零点s=-K_p/K_v，位于s平面的左半平面。系统可能有大的超调量和较长的稳定时间，随零点的位置而定。如图4-11所示为操作臂控制系统受到扰动（D（s））的影响的反馈控制框图。这些扰动是由重力负载和连杆的离心力引起的。由于这些扰动，电动机轴输出力矩的一部分被用于克服各种扰动力矩。由式（4-8）得出：

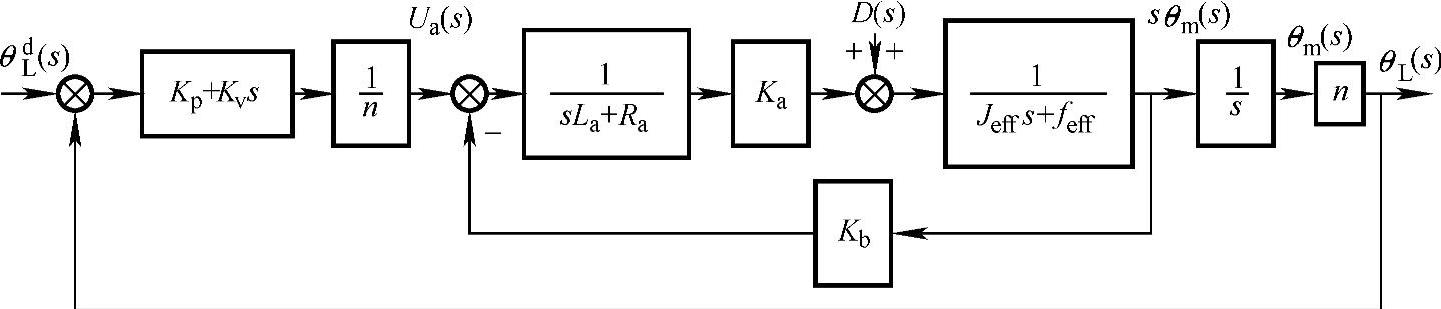
图4-11 操作臂控制系统受到扰动（D（s））的影响的反馈控制框图

只有扰动作用下，系统输出角位移的拉氏变换为

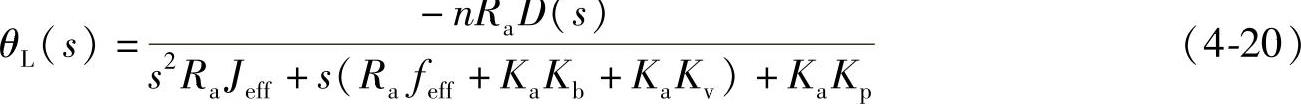
根据式（4-18）和式（4-20），运用叠加原理，从这两种输入可以得出关节的实际位移：

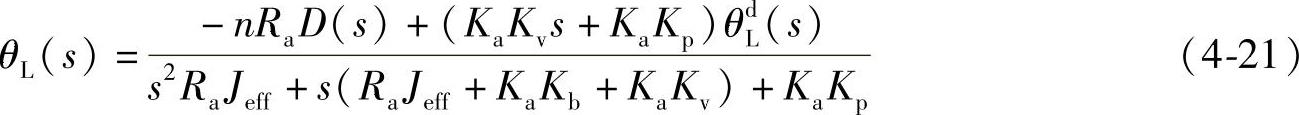
最重要的是上述闭环系统的特性，尤其是在阶跃输入和斜坡输入产生的系统稳态误差和位置与速度反馈增益的极限。